1300. 石英ガラスの耐薬品性
Date: Thu, 29 Aug 2013 07:29:50 +0900Q1: 東京農工大学 佐藤先生
小生O社の技術部Tと申します。
webに掲載される際は匿名にてお願い致します。
弊社は石英ガラスを扱っておりますが、質問は
洗浄工程で用いますNaOH、HCl、HFに対するガラスの耐薬品性についてです。
それぞれの溶液に対する溶解度を調査したわけではありませんが、 大きく分けてVADによる合成石英(低OH)、CVDによる合成石英(高OH)で 耐性に差があるような気がするのです。
そこで先生がもしこの点に関して知見をお持ちでしたら御教授賜りたくメールさせて頂きました。
面識もなく、大変不躾であることは承知しておりますが、何卒宜しくお願い申し上げます。
----------------------------------------------------------------------------------------------------------------
Date: Thu, 29 Aug 2013 12:07:38 +0900
A1: T様、佐藤勝昭です。
メールありがとうございます。私は石英ガラスについては専門外なのですが、取り急ぎご回答申し上げます。
大興製作所のホームページを見たところ
添付のような高純度透明石英ガラスの分析表があり、CVD製品はVAD製品に比べ、OH濃度だけでなくAl, Caなどの金属不純物濃 度も高いようです。VADとCVDの耐薬品性の違いは、この金属不純物によるのではないかと考えますが、T様のお考えはどうでしょうか?
----------------------------------------------------------------------------------------------------------------
Date: Thu, 29 Aug 2013 12:56:33 +0900
Q2: 東京農工大学 佐藤先生
早々の御回答有り難うございます。小生の言葉が少し足りませんでした。
もう少し詳しく申し上げますと、最近ではCVD材でも使用目的により非常に高純度になってきておりまして、 合成材とほとんど純度に置いては差のない物も御座います。
また、NaOHではOH含有量が多い方がHClではOH含有量が少ない方が溶解度が小さいような気がするのです。
石英ガラスに限らず、そのOH含有量と薬品の持っているOH基、H基とは何らかの関わりは有るのでしょうか。
一般的な知見でも結構です。何かお持ちでしたら御教授願えないでしょうか。
宜しくお願い致します。
----------------------------------------------------------------------------------------------------------------
Date: Thu, 29 Aug 2013 13:27:03 +0900
A2: T様、佐藤勝昭です。
石英ガラスのOH基は表面に付く場合と内部に入る場合があります。
(1)表面に付く場合はSi-OH、Si-OH-OH2などの形で表面を覆うので、NaOHに対する耐 性が増加し溶解度が下がります。一方、HClは表面のOH基と反応してH2Oが生じ、剥き出 しになったSi表面をClイオンがアタックします。
(2)内部に入る場合:石英ガラスのネットワーク構造は6員環Si-O基が基本ですが、 欠陥構造として3員環、4員環が生じていることがあります。OH基はこれらの欠陥構造 を減少させる傾向にあるとされています。HClの場合、HClを構成するH+がOH-と結合し て、欠陥構造が増加しているかも知れないですね。
粟津浩一:Water in silica glass; NEW GLASS Vol.21 No.3 p.6 (2006)を参考にしま した。
---------------------------------------------------------------------------------------------------------------
Date : Thu, 29 Aug 2013 16:58:47 +0900
AA: 東京農工大学 佐藤先生
参考になりました。有難うございました。
又、何かあればメールさせていただきます。
----------------------------------------------------------------------------------------------------------------
1301. ITOのエッチャント
Date : Fri, 13 Sep 2013 14:56:30 +0900Q: 大阪大学工学部4年 井口認です。現在、透明電極の作成・評価を行っております。
状況:MOCVD法で成長させたp-GaNの上にEB蒸着で電極材ITOを2nm、Agを200nm蒸着させています。
フォトリソグラフィーがうまく行かず、アセトンで電極を剥がす際に落ちてほしくない場所まで落ちてしまい失敗しました。
ここからp-GaNを節約するために、フォトリソグラフィーからやり直そうと考えています。
-----------------------------------
質問:そこで質問なのですが、ITO電極をGaN基盤からきれいに除去する方法はありますでしょうか?
35%塩酸で12時間以上、王水(35%塩酸と70%硝酸)で12時間以上それぞれ浸け置きしましたがどうしてもITOが残ってしまいます。
-----------------------------------------------------------------------------------------------------------------
Date : Sat, 14 Sep 2013 07:45:20 +0900
A1: 井口君、佐藤勝昭です。
4年生でがんばっていますね。卒研ですね。指導教員に聞かれたのですか。
ITOのエッチャントについては、多くの研究があります。
あなたのやっている塩酸+王水は2004年頃から行われています。
C.J. Huang et al.:The effect of solvent on the etching of ITO electrode; Mat.Chem.Phys.84146-150(2004)
しかし、古くからフッ酸が使われていたようです。
Shabbir A Bashar:Study of Indium Tin Oxide (ITO) for Novel Optoelectronic Devices; Ph.D. thesis University of London
Wet Chemical Etching of Metals and Semiconductors(Brigham Young University) のITOの項
やってみてはいかがですか。HFは怖いので、指導教員や先輩と相談して、十分注意してくださいね。
------------------------------------------------------------------------------------------------------------------
Date : Sat, 14 Sep 2013 16:46:22 +0900
A2: 井口君、佐藤勝昭です。
Facebookで質問しましたら、岩谷 素顕さんという方から
「ITOは通常は硝酸系に塩酸等を入れてエッチングしますが、条件によっては残ると思います。硝酸に硫酸アンモニウムとかを入れると残渣はほとんどないものが作れますが、面倒な場合は最近はITO専用のITOエッチャントというのが市販されているのでそちらを使われると安全かと思います。」
との回答をいただきましたので紹介しておきます。
------------------------------------------------------------------------------------------------------------------
Date : Sat, 14 Sep 2013 17:41:56 +0900
AA: こんばんわ。先日ITOについてお尋ねした井口です。フッ酸を使うか非常に悩んでおりました。
硫酸アンモニウムは当研究室に無いかもしれません(フッ酸はありますが...)ので、エッチャント液もしくは、硫酸アンモニウムを買ってもらえるよう担当教員にお願いします。
解答ありがとうございました。
------------------------------------------------------------------------------------------------------------------
Date : Sat, 14 Sep 2013 20:24:13 +0900
A3: 井口様、佐藤勝昭です。
岩谷さんから追加の情報です。
「硫酸アンモニウムがなければ、ITO用のエッチャント液を買われると良いと思います。確か多結晶用とアモルファス用があったと思います。詳しくは薬品メーカの人と相談すると希望する物が買えると思いますと質問者に回答いただくと良いかと思います。」
とのコメントがFacebookに書き込まれました。参考にしてください。
--------------------------------------------------------------------------------------------------------------------
1302. GaAsの光学定数
Date : Wed, 25 Sep 2013 05:00:09 +0900Q1: 科学技術振興機構 佐藤勝昭 先生
長らくご無沙汰致し,失礼致してております.
少し前にGaAs などの屈折率の貴重なデータを先生から頂ました電気通信大学の冨田でございます.
現在,GaAs基板表面に周期構造を形成した場合の太陽光の電力透過係数について数値解析を行っています.
そこで,先生にご教示して頂きたい点があり,失礼をも顧りみずお尋ねする次第です.
先生から頂ました,GaAsの入射光の波長にたいする屈折率のデータでは,いわゆる,テンソルでは無く,1つの波長に対して,スカラ量として,1つの屈折率の実数部と虚数部の値が列挙されています.インターネットでも調べましたが,やはり,同様に表示されていました.太陽電池を構成するGaAs基板を単なる等方的分散性を有するⅢーⅤ族化合物半導体として波動光学的にスカラ解析しても差し支えない,と言うこでしょうか.
それとも,太陽光セルはGaAs結晶基板で構成されているが,その結晶構造が,閃亜鉛鉱型の構造をしているので,近似的に等方的分散性媒質と考え,GaAs結晶基板がx,y,z 方向の屈折率が等しい分散性媒質であるとして,スカラ解析しても差し支え無い,と言うことでしょうか.色々と調べましたが判然と致しません.
ご多忙中,誠に恐縮ですが上記のことについてご教示下さいます様お願い申し上げます.
---------------------------------------------------------------------------------------------------------------------
Date : Wed, 25 Sep 2013 09:43:57 +0900
A1: 富田先生、佐藤勝昭です。GaAsはじめⅢ-Ⅴ族化合物は、基本的に閃亜鉛鉱構造なので等方的と考えてよいと考えられています。しかし、エピタキシャル成長した薄膜では、臨界膜厚以下の厚さではコヒーレント成長するため面内と面直で格子定数が異なる「一軸異方性」が誘起されます。この結果光学異方性が現れますが、この値は格子不整合と熱膨張差の関数なので、成長条件次第です。数値計算では等方性からのずれをパラメータとしてフィットするしかないでしょうね。
----------------------------------------------------------------------------------------------------------------------
Date : Wed, 25 Sep 2013 15:06:57 +0900
Q2: 佐藤勝昭 先生:
ご多忙中,早速ご回答を頂き,誠にありがとうございました.
今回の私共の数値計算では,半無限の真空領域と同じく半無限のGaAs媒質が接していると言う仮定の下で,GaAs表面に周期的な溝構造を形成し,真空中から太陽光が入射する場合の電力透過量を数値解析致しました.その際,先生から頂いたデータやインターネットで検索したデータを用いました.
インターネットで検索したデーターもテンソル量では無く,単にスカラ値としての屈折率値が示されていました.従って,不勉強で大変恥ずかしいのですが,一般に用いれているソーラーセルではGaAsの結晶では無く,化合物半導体としてのGaAsを使用しいると言うことでしょうか.
今回の様な数値計算をする場合は,エピタキシャル成長させたGaAsの薄膜を解析の対象としていませんので,先生のご回答の如く等方性媒質としての屈折率(分散性の複素屈折率)を用いて数値計算しても良いと言うことでしょうか.
ご多忙中,大変恐縮で申し訳ございませんが,再度,ご教示下さいます様お願い致します.
尚,解析の結果,GaAs 表面に周期構造を形成すれば,太陽光の全波長帯域に亘って太陽光の電力透過量がかなり,増加することが判明致しました.
以上,宜しくお願い致します.
----------------------------------------------------------------------------------------------------------------------
Date : Wed, 25 Sep 2013 15:39:18 +0900
A2: 冨田先生、佐藤勝昭です。
「一般に用いれているソーラーセルではGaAsの結晶では無く,化合物半導体としてのGaAsを使用しいると言うことでしょうか」の意味が不明です。
GaAsはGaとAsの化合物なのでソーラーセルに限らずHEMTに使われるGaAsも化合物半導体と呼ばれます。
またGaAsは非晶質は使われることはなくすべて(エピタキシャル薄膜も含め)単結晶が使われます。
-----------------------------------------------------------------------------------------------------------------------
Date : Thu, 26 Sep 2013 04:40:33 +0900
Q3: 佐藤勝昭 先生:
ご多忙中,度々お手数をお掛け致しまして申し訳ございません.様々にご教示頂き誠にありがとうございました.不勉強で恥ずかしい限りです.私は電磁波の散乱問題の解析および解析法の開発を専門として,これ迄研究してまいりました.従って,結晶については全く門外漢です.
しかし,この度,太陽電池の発電効率を物性的に上げるのではなく,素子表面における太陽光の透過効率を上げるため素子表面に波長オーダーの周期構造を形成した場合の透過効率の増加を期待して,波動光学的に数値解析してみました.その解析では,GaAsを等法的な分散性媒質として回折問題を解き,論文を作成致しましたが,GaAsが結晶ならば,異方性を考慮しなっくても良いのだろうかと,かねてより考えていました.そこで,先生にお尋ねした次第です.
先生のご回答では,臨界膜厚以下でエピタキシャル成長させたGaAs結晶では,一軸異方性を有する結晶であるとのことでした.今回,解析したモデルでは,GaAs媒質(結晶)の膜厚は大変厚い(半無限)と仮定し,ただ,その表面に周期構造を形成した 場合の太陽光(平面電磁波と仮定)の透過,反射現象を解析しています.従って,この解析においては,厳密ではないかもしれませんが,近似的に等方的な媒質として解析しても差し支えないと推察されますが,間違っているでしょうか.
最後にお尋ねしたい点は,インターネットなどでSiやGaAsの屈折率を調べますと,Siの場合は波長によっては,屈折率が2つ与えられていすますが,GaAsについては,1つの波長に対して1つの屈折率しか表示されていません.やはり,一般的には,GaAsは,等方性媒質として取り扱われているのでしょうか.
以上,大変長々と文章書き申し訳ございません.今後共ご指導下さいます様お願い致します.
-----------------------------------------------------------------------------------------------------------------------
Date : Thu, 26 Sep 2013 07:22:16 +0900
A3: 冨田先生、佐藤勝昭です。
太陽電池の表面に微細構造をつけて効率を高くする技術は、1970年代から研究されております。現在の多くの太陽電池は反射防止膜と共に微細構造(テキスチャー)を使っています。
そのような現実のことをお調べになってから論文にされるとよいと思います。私の「太陽電池のキホン」などをお読みください。
ps.シリコンもGaAsも立方晶なので等方性です。データに2つあるのは、測定によってばらつくからです。
-----------------------------------------------------------------------------------------------------------------------
Date : Fri, 27 Sep 2013 00:42:58 +0900
AA: 佐藤勝昭 先生:
この度は,大変お世話になり,誠にありがとうございました.私はこれまで誘電体格子による解析問題を解析してきましたので.太陽電池素子表面に周期構造を付け太陽光の透過電力について実験的に調査して,特許などとして多数報告されていると認識しています.
しかし,私の不勉強かもしれませんが,電磁波の散乱問題として理論的に解析し,定量的に透過量について議論した論文は,まだ,報告されていないと思います. 太陽光電池の発電効率を上げるためには,物性的な改良も当然必要ですが,広い帯域を有する太陽光電力をまず,全帯域に亘って,可能な限り透過させることが必要であると考え,解析した次第です.周期構造の溝の深さを増し,周期構造を工夫すれんば,太陽光の全帯域に亘る入射電力の70%以上の電力を透過させることが可能であると考えられます.
------------------------------------------------------------------------------------------------------------------------
1303. 電磁波による非破壊検査
Date : Mon, 7 Oct 2013 09:08:47 +0900Q: 佐藤勝昭 様
お世話になっております。
S*大学大学院のY*と申します。
佐藤様のHPを拝見し、質問させていただきたいと存じます。
以前にも何度か質問させていただき、丁寧なご回答を頂戴いたしました。
その節は誠にありがとうございました。
今回も勝手ながら無知な質問をさせていただくことをお許しください。
今回は電磁波の非破壊検査についてお聞きしたいです。
また今回も匿名でお願いいたします。
質問は2点です。
①なぜ電磁波の非破壊検査ではエックス線以上の周波数以外は使用しないのでしょうか。
エックス線の特性を考えるとエックス線を使用する意味はわかるのですが、
例えば可視光やもっと低い周波数を使用することはできないのでしょうか。
②電磁波の非破壊検査には弱点はないのでしょうか。
私が知る範囲では、一部の材料においては、表面の微細な欠陥は認識できない場合があることはわかりました。
他には欠点はありませんでしょうか。
また佐藤様が今後の電磁波の非破壊検査に期待することがあれば教えてください。
以上になります。
長文になってしまい申し訳ございません。
お忙しいとは存じますが、何卒ご回答のほどよろしくお願い申し上げます
------------------------------------------------------------------------
Date : Mon, 7 Oct 2013 23:49:43 +0900
A: Y君、佐藤勝昭(仙台出張中)です。
①なぜ電磁波の非破壊検査ではエックス線以上の周波数以外は使用しないのでしょうか
対象物によって、いろいろな周波数が使い分けられます。
遺跡の調査や資源の探査にVHF帯からSHF帯の電波が使われています。例えば 地下遺構の可視化(亀井宏行) によれば、波長が短い程分解能が上がることがわかります。
半導体の中の不純物を非破壊で同定する手段として、電子スピン共鳴がありますが、こ れにはマイクロ波が使われます。また、赤外吸収分光やラマン散乱分光、蛍光分光など 光による欠陥等の非破壊評価が行われています。
脳や心臓など体の中を観るMRI(磁気共鳴画像診断装置)はVHF帯の電波が使われます。 最近、空港での荷物の非破壊検査にテラヘルツの電波が使われます。プラスチック爆弾 や有機溶媒など危険な物質を同定することができるからです。
半導体結晶の非破壊検査には赤外~可視のレーザ光を用いた「光散乱トモグラフィー」 が使われます。
お札が偽札かどうかを判定するために、磁気インクで書かれた数字や画像からの磁束を 磁気光学結晶に転写して、磁気光学効果で非破壊に検査することも行われています。 極紫外線による光電子分光も物質の同定のためによく使われています。
このように、君の調べ方が不十分なだけで、あらゆる波長帯の電磁波が用いられています。
②電磁波の非破壊検査には弱点はないのでしょうか。
分解能は、電磁波の波長の程度しかありません。ただし、近接場を用いたり、超解像 技術を用いると波長の数分の一の小さなものを 観測できます。調べたい欠陥の大きさ に合わせて、電磁波の波長を選ぶ必要があります。
---------------------------------------------------------------------------
Date : Tue, 8 Oct 2013 20:11:36 +0900
AA: 佐藤様、先日質問させていただいたS大学のYです。
出張中にも関わらず、早速ご回答していただき本当にありがとうございました。
また、私の調べが不十分なためにくだらない質問をしてしまいましたこと大変申し訳ございませんでした。
今後はこのようなことがないようきちんと自分で調査してから次の行動を起こすように致します。
しかし貴重なご意見をいただいたことまたご丁寧な回答をいただき、誠にありがとうございました。
今後の研究活動に必ず活かしたいと存じます。
----------------------------------------------------------------------------
1304. UV-LEDの光軸の見つけ方
Date : Sun, 13 Oct 2013 00:23:43 +0900Q: 東京農工大学、佐藤先生
初めまして、V社の七瀬と申します。
UV-LED(NSSU100C)について質問させてください。
日亜化学製のUV-LED(NSSU100C)から発光するUV光には光軸という概念が存在するのでしょうか?
この光軸の向きを調べたいのですが、どのような方法が考えられますでしょうか?
-----------------------------------------------------------------------------
Date : Sun, 13 Oct 2013 01:57:49 +0900
 A: 七瀬様、佐藤勝昭です。
A: 七瀬様、佐藤勝昭です。LEDがGaNのc面を使っている場合は、偏光特性は殆ど無いと思います。
日亜の製品ではありませんが、豊田合成の青色LEDでm面のGaNを使ったものにおいて、 添付図のような偏光特性が報告されております。 (豊田合成の発表による。)
m-面だけでなくa-面を使ったLEDも偏光性があると考えられます。LEDからの光を偏光子(紫外線領域で使えるもの)を通して光検出器に照射し、偏光子を回転させたときに最大の強度を与える偏光子の方位が光軸と考えてよいでしょう。
----------------------------------------------------------------------------
Date : Sun, 13 Oct 2013 21:42:35 +0900
A':七瀬様、佐藤勝昭です。 Facebookであなたの質問と私の回答を公開しましたところ、名城大学准教授の岩谷素顕先生から
「日亜のLEDは基本的にはc面成長なので偏光特性はないと思います。もっと言うと、市販されているLEDでc面以外のものは日本では手に入らないと思います。」
というコメントをもらいました、参考にして下さい。
----------------------------------------------------------------------------
Date : Mon, 14 Oct 2013 00:20:14 +0900
Q2:佐藤先生、ありがとうございます。
偏光状態でないということは、光軸は基本的にはまっすぐと理解してよいのでしょうか。
--------------------------------------------------------------------------------
Date : Mon, 14 Oct 2013 09:23:41 +0900
 A2: 七瀬様、佐藤勝昭です。
ごめんなさい。ご質問は偏光を表す光学軸(optic axis)ではなく、光の進行方向を
表す光軸(optical axisi)のことだったのですね。後者に関しては、偏光は全く関係あ
りません。
A2: 七瀬様、佐藤勝昭です。
ごめんなさい。ご質問は偏光を表す光学軸(optic axis)ではなく、光の進行方向を
表す光軸(optical axisi)のことだったのですね。後者に関しては、偏光は全く関係あ
りません。マニュアルに光の指向特性が出ています。
添付図は指向性をあらわしています。これによれば、まっすぐに進むはずです。
しかし、図はあくまでLED素子自体の指向性であって、マウンティングしたあとのケースとの角 度があれば、当然のことながら進行方向はケースの中心軸からずれるでしょう。この場 合は、LEDを傾斜度の変えられるゴニオメータにマウントして、根気よく角度依存性を 測定して、最大になる方向を決めるしかないですね。
---------------------------------------------------------------------------------
1305. 不動態皮膜の耐酸性と導電性の両立
Date : Thu, 17 Oct 2013 10:34:28 +0900Q: 佐藤勝昭先生
先生のホームページを拝見し、初めてご連絡致します。
T*社のA*と申します。
早速ですが、不動態皮膜の耐酸性と導電性の両立に関連して何点か お聞きしたいことがあります。ご教授いただけましたら幸いです。
1.不動態皮膜を除去してからその部分に導電塗装をした場合でも不動態皮膜は成長していくものでしょうか。(抵抗が増えていくものでしょうか)
2.不動態皮膜の成長は時間、温度など何に多く影響されるのでしょうか。 (仮に上記工法で部分的な導通が確保出来るとしたら)不動態皮膜は部分的に除去してもすぐに再生されるようですが、作業経過時間とともに抵抗がどのように増えていくかを知りたいと思います。
以上、よろしくお願い致します。
----------------------------------------------------------------------------------
Date : Sat, 19 Oct 2013 12:41:31 +0900
A: A様、佐藤勝昭です。
ステンレスの不動態のことでしたでしょうか?表面の不動態はクエン酸で処理することで鉄を溶かしてクロムの酸化物を形成しています。
機械的に研磨してやれば不動態は除去出来るのでその上に金属を堆積すれば導電性が確保できます。
ご質問は、その後再び界面に不動態が出来て導電性が悪くなるかということですね。
上に着けた金属とステンレスの界面の密着性がよければ、不動態の形成は、起きないと思います。
ただし、長期的には上に着けた金属を通して酸素が侵入してステンレスを酸化させる可能性があります。
しかし非常に薄いので、電子はトンネル効果で透過するので抵抗は高くならないと存じます。
----------------------------------------------------------------------------------
Date: Mon, 28 Oct 2013 11:36:17 +0900
AA: 佐藤勝昭先生
お世話になっております。
質問にご回答をいただきまして有り難うございました。
お返事はこないものと思いながら、問い合わせたもので大変有り難かったです。
遅くなりまして大変恐縮ですが、まずはお礼まで。
-----------------------------------------------------------------------------------
1306. 金属の吸収スペクトル
Date : Fri, 18 Oct 2013 19:09:58 +0900Q: はじめまして。お忙しいところメールで失礼致します。
T*大学3年のN*と申します。
今回、私は金属の吸収スペクトルのデータを探しているのですが、化学便覧、物理定数表などを見ても何点かの波長に対する反射率が載っているだけで 可視光域全体を曲線で結んだ吸収スペクトルのデータというものが見つかりません。
インターネットで検索している際に、佐藤先生のHPに辿り着き、先生なら何かアドバイスを貰えるのでは、と思い今回メールをさせて頂いた次第です。
各元素について金属単体の可視光域の吸収スペクトル(なければ反射スペクトルでも大丈夫です)が一覧として載っているHPまたは本などをご存知でしょうか?
時間があるときにでも返信いただけると助かります。
----------------------------------------------------------------------------------
Date : Sat, 19 Oct 2013 20:46:08 +0900
A: N君、佐藤勝昭です。
金属の吸収スペクトルのデータが見つからないのは、金属はよほど薄い膜にしない限り光が透過しないので、 半導体のような光透過スペクトルから求める方法がとれないからです。
そこで、金属に光を当てて反射スペクトルをとって、それからクラマースクローニヒ解析を使って光学定数 (屈折率n・消光係数κ)を求める方法や、分光エリプソメトリー法を使って、ΨとΔを求め、これから直接光学定数nとκを求めます。
消光係数κと吸収係数αの間には、α=4πκ/λの関係があるので、κと波長λがわかれば吸収係数αを求めることができるのです。
金属の光学定数n,κは、下の書物に載っています。図書館で調べて下さい。
Palik:Handbook of Optical Constants in Solids, I, II (Academic)
Landolt Boernstein:New series III-15b (Springer)
工藤恵栄:分光学的性質を主とした基礎物性図表(共立、昭和47):絶版
また、私のなんでもQ&Aにも関係するQ&Aがありますよ。
5. 金属の反射スペクトル
47. 光学定数の抽出法
394. 金属による光吸収
646. 金、銀、Ni、Al、Cuの反射率
----------------------------------------------------------------------------------------
Date : Sun, 20 Oct 2013 00:43:38 +0900
AA: 返信ありがとうございます。
Q&Aに類似した質問があったようですね。調べが足りずお手数かけてすみませんでした。
しかし、直接回答して頂いたことに感謝すると同時にうれしくもあります。
教えて頂いた文献を早速探してみます。
その際に新たな質問が生まれたら、また質問させていただくかもしれません。
迅速かつご丁寧な回答ありがとうございました。
----------------------------------------------------------------------------------------
1307. 赤外透過率を用いたガス濃度定量
Date : Tue, 5 Nov 2013 08:16:25 +0000Q1: 佐藤勝昭様 K*社 M*と申します。たびたび佐藤様のHPを拝見させていただいておりましたが、今回初めてメールさせていただきます。
なお、お手数ではございますが、Webに掲載の際には会社名、氏名ともに匿名にてよろしくお願いいたします。
赤外透過率測定を用いたガス濃度の定量について教えていただきたく今回メールさせていただいております。
NISTのデータベース(http://webbook.nist.gov/chemistry/name-ser.html)に載っているIR透過スペクトラムの データから波長毎の吸収係数を算出したいのですが、透過スペクトラム測定時の濃度の考え方に少し混乱があり、 質問させていただく次第でございます。
ガスが大気圧下に存在するときに濃度(体積濃度)と、IR透過率の関係を求めるのが目的です。
(ただし、光源、バンドパスフィルタともにブロードなものを想定しておりますので、細かな吸収線まで 見る必要はありません)
透過スペクトラムデータの測定条件は下記が記載されておりました。
150mmHgの圧力のガスを窒素希釈して全圧600mmHgの圧力で測定、光路長は5cm (温度条件の記載なし)
吸収係数をε、濃度c、光路長Lとして
-Log(透過率)=ε x c x L
の関係からεを求めることができると思いますが、濃度c(体積濃度、ただし大気圧下での)の求め方として、
c = 150 / 760
で正しいでしょうか?(760は760mmHg = 1atmという意味です)
(本来は温度条件が入ってくると思いますが、ここでは無視しています)
IRスペクトラム測定時の600mmHgという数字は、少なくとも今回の目的においては、濃度算出には関係ないと思っているのですが、 今一つ自信がありません。
お忙しいところ申し訳ありませんが、ご教授いただければ幸いに存じます。
以上、よろしくお願いいたします。
-------------------------------------------------------------------------------------
Date : Tue, 5 Nov 2013 18:40:03 +0900
A1: 森本様、佐藤勝昭です。
ある体積たとえば1m3の箱に150mmHgの被測定ガスと450mmHgのN2ガスを入れて全圧600 mmHgにしたとすれば、被測定ガスは、モル比で25%に薄められたものと見なせます。吸 収係数εはガス固有のものですからこのガスについて-Log(透過率)=ε x c x Lの式か ら濃度cを求めたとしたら、薄めたガスの濃度が出たと考えられますから、本当の濃度 はcを4倍する必要があるのではないでしょうか。
-------------------------------------------------------------------------------------
Date : Tue, 5 Nov 2013 10:48:38 +0000
Q2: 佐藤様
K社 M本です。
お忙しい中、早速のお返事ありがとうございます。
私の最初のメールで濃度cの求め方をお聞きしているのですが、これは、
本当に求めたいものは吸収係数であり、吸収係数を求めるために式に代入する濃度cの考え方を どうしたらよいか、をお聞きしているつもりでした。そして濃度cの次元としては大気圧下でのガス濃度 (体積濃度)を使いたく、そのためには、与えられている測定条件の数値をどう使えばよいか、を お聞きしているつもりでした。
分かりにくい表現になってしまい申し訳ありません。
今回モル比25%(被測定ガス150mmHg, N2ガス450mmHg)のガスを使って 光路長L=5cmのセルでIR透過率測定し、波長毎に透過率のデータが得られています。
ここから吸収係数を計算する際に、N2の有無は吸収係数計算には 関係ないのではないか(被測定ガス分圧150mmHgだけが関係するのではないか)、と 考えています(ある体積の中に何個の被測定ガス分子があるか、が関係するのではないか)。
このため、大気圧下での体積濃度としてcを表現するとき、被測定ガス分圧150mmHgを 1気圧で割ればよいのではないかと考えた次第です。
お忙しい中、大変恐縮ですがよろしくお願いいたします。
-------------------------------------------------------------------------------------------
Date : Wed, 6 Nov 2013 18:16:38 +0900
A2: 森本様、佐藤勝昭です。データは透過率の値が掲載されているのですね。吸収係数αは 、α=-(lnT)/Lで与えられます。モル吸光度に直すにはセル中の気体のモル濃度で 割ります。測定ガスのモル濃度は分圧と比例関係にあるのでお考えのように150mmHgを 使ってよいと思います。
-------------------------------------------------------------------------------------------
Date : Wed, 6 Nov 2013 10:14:52 +0000
AA: 佐藤様、K社Mです。
お返事ありがとうございます。
モル吸光度を求めるにはモル濃度用い、モル濃度は分圧と比例関係にある、ということで、希釈有る無しに関わらず150mmHgを使えばよい、ということですね。
今回はお忙しい中、私の質問に答えてくださり本当にありがとうございました。今後ともよろしくお願いします。
そろそろ寒い季節となってまいりました。どうかご自愛ください。
それでは失礼いたします。
--------------------------------------------------------------------------------------------
1308. フェルミエネルギーについて
Date : Wed, 6 Nov 2013 00:06:11 +0900Q1: はじめまして、T*大学物理学科2年のS*と申します。
HP掲載の際には匿名でお願いします。
固体物理などでは、必ずフェルミエネルギーというのが出てくると思いますが、教科書などで読んでもイマイチそのメリットがわからないです。
フェルミエネルギーを考えることが何の役に立つのでしょうか?
また各元素のフェルミエネルギーは計算で求める際、
Ef=(h2/2m)×(3n/8π)(2/3)
以上のような式で書け、nが電子総数で、以下のように書けるはずです。
n=0.6022×1024×(Zρ/A)
Zが価数だと思うのですが、金属のような複数の価数をとれるものになると、
金属固体中の価数はどれを選べばいいのでしょうか?
また電子総数が記されてる書物をご存じでしたら教えてもらえないでしょうか?
----------------------------------------------------------------------------------------------
Date : Wed, 6 Nov 2013 22:32:01 +0900
A1: S君、佐藤勝昭です。
(1) フェルミエネルギーのメリット
・金属のフェルミエネルギーは、金属のバンドのどこまで電子が占有しているかを表し ています。金属において電気伝導に寄与するのは、フェルミ面付近にある電子のみです。
フェルミ面から電子を真空準位に取り出すためのエネルギーを「仕事関数」といいます。
・金属と半導体の接合においてショットキー障壁ができますが、その高さは、電子を 金属から取り出して、半導体にくっつけるために必要なエネルギーなので、金属の 仕事関数から、半導体の電子親和力を引いたものとなっています。
・最近話題の磁気トンネル素子(MTJ)はハードディスクの記録読み出し磁気ヘッドに使 われています。
磁気トンネル効果とは、薄い絶縁層を2つの磁性金属で挟んだとき、磁性金属のフェル ミ面における電子のみがトンネル効果で通り抜けるのですが、そのとき、フェルミ面の電子のスピン が平行か、反平行かで伝導度が異なることを利用しています。(学部2年生には難しいでしょうね。)
(2) 金属固体中の価数
・フェルミエネルギーを求める式Ef=(h2/2m)×(3n/8π)(2/3)のnですが、金属の電 子のうち外殻電子の数のみが関与します。外殻電子がいくつあるかは、丸善「理科年表 」の物理/化学の「原子、分子、原子核」のページに「自由原子およびイオンの核外電 子という項目に書かれています。
例えば、Na [Ne]3s, Mg [Ne]3s2, Al [Ne]3s2 p, Si [Ne]3s23p2・・・という風 に書いてあります。[Ne]はNeの閉殻つまり1s22s22p6電子配置です。 外殻電子数はNaでは1, Mgは2, Alは3, Siは4です。
----------------------------------------------------------------------------------------------
Date : Thu, 7 Nov 2013 10:47:27 +0900
Q2: 佐藤勝昭先生
親切かつ詳しい説明ありがとうございます。
ちなみになのですが、フェルミ準位と元素の最外殻軌道エネルギーは関係があるのでしょうか?(フェルミ準位の高さや反応のしやすさなど)
-----------------------------------------------------------------------------------------------
Date : Thu, 7 Nov 2013 12:52:03 +0900
A2: S君、佐藤勝昭です。
原子の状態の場合、外殻電子は原子核のもつ正電荷とのクーロン相互作用によって強 く束縛されていますが、凝集して固体になって周期ポテンシャルの中に置かれると、電 子は束縛をはなれ、隣接原子、さらには第2隣接原子へと広がりますが、この電子のマ イナス電荷によってクーロン相互作用が遮蔽され、束縛がさらに弱くなって、結晶全体 に広がるのです。このため、フェルミエネルギーは、原子における束縛エネルギーより かなり小さくなっています。
-----------------------------------------------------------------------------------------------
Date : Fri, 8 Nov 2013 03:38:52 +0900
Q3: 連絡遅れてしまい申し訳ございません。
理科年表で確認したのですが、先生がおっしゃった自由原子およびイオンの核外電子という項目が見つからず、 原子およびイオンの電子配置のことではないのかと思いました。間違っていたらすみません。
それで、金属固体の価数の考え方についてですが、これを遷移金属で考えると、d電子を考えず、s電子を価数と考え、 ほとんどが1価、2価で固体中に存在するということでしょうか?
そうなると、PdとPtではs電子が0個(solid state physics,Ashcroft Mermin著より)で価数をもたず、 伝導電子がないことになってしまうような気がするのですが、これはどのように考えればよいのでしょうか?
------------------------------------------------------------------------------------------------
Date : Fri, 8 Nov 2013 09:10:56 +0900
A3: S君、佐藤勝昭です。
私は古い(1990年の)理科年表を使っているので、項目が違っていてごめんなさい。
確かに、Pdは[Kr]4d10であって、原子にはs電子がなくd電子も全部埋まっていて伝導 電子がないように見えますが、固体中ではs軌道が下がってきて、d電子と混成します。
また、Pdのフェルミ面は5s-4dバンドの中に来るようです。Pt原子は[Xe]4f14 5d9 6s となっており、5dに孔が空き6sに電子が来ています。
PdやPtの固体中のd電子はかなり広がっているので、伝導電子として寄与します。いず れにせよ原子と固体ではずいぶん電子状態は異なりますよ。
-------------------------------------------------------------------------------------------------
Date : Sat, 9 Nov 2013 00:32:55 +0900
Q3: 返信遅れてすみません。そうなると、プラチナやパラジウムのフェルミエネルギーはどのようにして求めるもの何でしょうか?
何度も質問してすみません。
--------------------------------------------------------------------------------------------------
Date : Sat, 9 Nov 2013 08:26:52 +0900
A3: S君、佐藤勝昭です。
実際の物質の電子状態は、あなたが学んだ放物線型ほど簡単ではありません。面倒な バンド計算をするのですが、ベースになる波動関数は、もはや原子由来のs電子、d電子 などではなく、混成した複雑な軌道になっています。sとかpとかdとかいうのは、あく まで原子のポテンシャルのもとでの、軌道角運動量の固有値による分類ですが、固体結 晶中では、軌道角運動量はもはやよい量子数ではありません。
添付図は、Ptのバンド構造と状態密度です。この複雑な状態密度曲線を積分して、フェ ルミエネルギーを求めるのです。
--------------------------------------------------------------------------------------------------
Date : Sat, 9 Nov 2013 18:16:31 +0900
AA: 詳しい解説ありがとうございます。
やはり実際はそう簡単にいくものではないようですね。
これを足がかりにして日々精進していきたいと思います。
何かあったらまた、よろしくお願い致します。
--------------------------------------------------------------------------------------------------
1309. 金属の光学定数(複素屈折率)の温度変化
Date: Thu, 14 Nov 2013 14:58:42 +0900Q1: 佐藤勝昭 様
はじめまして。お忙しい中メールで失礼します。
私、新潟工科大学4年の南 沙斗紫と申します。 私は大学の研究室にて次世代記録方式の熱アシスト磁気記録に用いられる近接場光素子の研究をしております。
近接場光素子は金属(主に用いる金属はAu、Ag、Alの3つ)の薄膜です。
私は近接場光素子のFDTD解析を主にしております。
その解析を行うなかで解析を行うプログラム上に近接場光素子として用いる金属の物性値を入力します。
物性値は、屈折率と複素屈折率です。
屈折率と複素屈折率は解析に用いるレーザーの波長によって異なります。
さらに屈折率と複素屈折率は温度によっても変化するようです。
温度によってどのように変化するかいろいろ調べても参考になるようなものがなく困っている状況です。
物性値に関することインターネットで検索していると、たびたび佐藤先生のHPをお見受けします。
そこで佐藤先生なら有力なアドバイスが貰えるのではないかと思いメールさせていただきました。
お忙しいところ申し訳ありませんが、屈折率と複素屈折率の温度による関係についてご教授いただければ幸いです。
わかりにくい文章になったかもしれませんが、何卒よろしくお願いします。
------------------------------------------------------------------------------------------------
Date: Thu, 14 Nov 2013 16:49:55 +0900
A1: 南君.佐藤勝昭@新幹線(携帯より)です。
ご質問は複素屈折率の実数部nと虚数部kの温度依存性ですね。熱アシスト記録の温度はせいぜい500Kなので複素屈折率の変化は無視出来ると思います。
金属の光学応答は殆どプラズマ周波数で決まっているのですが、これは自由電子の密度で決まります。
固体物理学で学ばれたように金属の自由電子密度は殆ど一定と考えられています。
スペクトルの詳細は電子のフォノン散乱による緩和時間の増加のため変化するでしょうが熱アシスト記録の解析においては、無視出来るのではないでしょうか。
勿論融点近くまで加熱すれば、結晶構造が保たれないので、複素屈折率は大きく変化するでしょうね。
------------------------------------------------------------------------------------------------
Date: Thu, 14 Nov 2013 17:05:36 +0900
Q2: 佐藤勝昭 様
新潟工科大学の南です。お返事いただけて光栄です。
先ほどのメールでは"消衰係数"のことを誤って"複素屈折率"と書いていました。
しかしお聞きしたかった内容が伝わっていて良かったです。
私が解析に用いているレーザーの波長は180nm~900nmなのですが、波長に関係なく複素屈折率の変化は無視できるのでしょうか?
-------------------------------------------------------------------------------------------------
Date: Thu, 14 Nov 2013 19:58:10 +0900
A2: 南君、佐藤勝昭(@相生 SPring-8に出張中)です。 金属の反射率の温度変化に関する質問がすでに「物性なんでもQ&A#480」に載っています。
プラズモン周波数より長波長の光に対しては、ここに書かれていることを参考にして、やってみられるとよいでしょう。
短波長の光においてはバンド間遷移がきいてきます。
また実際の金属の場合(特にAg, Alでは)高温になると表面が酸化し特に短波長では、見かけの屈折率が変化します。
あなたの場合はシミュレーションをやっているだけなので酸化とかは気にしなくてよいでしょうが・・
プラズモンに関しては、私の書いた「プラズモンの基礎」を参考にして下さい。
------------------------------------------------------------------------------------------------
Date: Fri, 15 Nov 2013 09:27:31 +0900
AA: おはようございます。
返信が遅れてしまい申し訳ないです。
すでに類似したQ&Aがあったようですね。お手数かけてすいません。
この度はいろいろとお世話になりありがとうございました。プラズモンについても勉強しようとおもいます。
また質問させていただくことがあるかもしれませんが、その時はよろしくお願いします。
本当にありがとうございました。
------------------------------------------------------------------------------------------------
1310. Al2O3基板上にエピタキシャル成長したZnOの結晶性
Date : Wed, 20 Nov 2013 00:42:18 +0900Q: はじめまして、D*大学大学院修士2年のO*と申します。
佐藤先生のHPを拝見させていただいておりましたが、今回初めてメールさせていただきます。
なお、お手数ではございますが、Webに掲載の際には大学名、氏名ともに匿名にてよろしくお願いいたします。
早速質問になるのですが、現在MOCVDでZnOを作製しております。サファイア基板(006)に500℃で成長しています。
PL測定において室温では380nmを中心とした紫外発光のピークを確認できるのですが、深い準位からのブロードなピークは現れませんでした。
これは欠陥が少なく結晶性の高い試料なのかと思っていたのですが、XRDによるロッキングカーブ測定では(002)の半値幅が1.5~2.0°でした。
この場合結晶性は良いのか悪いのか判断がつかなく先生のアドバイスをいただきたいです。
お忙しいかと思いますがよろしくお願い致します。
------------------------------------------------------------------------------------------------
Date : Wed, 20 Nov 2013 01:13:45 +0900
A: O君、佐藤勝昭です。
匿名希望と言うことは、先生に聞けない事情があるのでしょうか?
私が指導教員だったら、研究室の学生が自分を差し置いてほかの先生に質問して いたら「自分は学生に信用されていないのだな」と悲しい気分になりますよ。
ヒントだけ差し上げましょう。Al23(001)基板上へのMOCVDによるZnO薄膜については
W.I. Park et al.: Metal-organic vapor phase epitaxial growth of high-quality ZnO films on Al2O3(00?1): J.Mater.Res. 16 (2001) 1358
を読んでください。
この論文では基板温度500℃でロッキングカーブの半値幅は0.19°が得られ、pole figureではきれいな6回対称が得られ、deep levelの発光も、励起子ピ ークの3桁以上低いレベルとなっています。励起子の線幅も7meVと鋭く、結晶性のよいエピ膜ができています。
-------------------------------------------------------------------------------------------------
Date : Wed, 20 Nov 2013 02:27:58 +0900
AA: 佐藤先生、Oです。
夜遅くお返事ありがとうございます。
研究室の指導教員と話はきちんとしているのですが、教授からは高品質な結晶ができているのではという意見をいただきました。
他の方の意見も少し聞いてみたいと安易に思ってしまいメールしてしまいました。申し訳ありません。
ヒントの論文ありがとうございます。
やはりrocking curveとPLのdeep level はどちらもいいようですね。
自分の試料と比べると、やはり自分の試料のrocking curveの半値幅が大きすぎるのが問題に感じました。
もう少し頑張ってその原因を調べて見ようと思います。
-------------------------------------------------------------------------------------------------
1311. 金属の酸化による機械的性質の変化
Date : Tue, 26 Nov 2013 15:05:22 +0900Q1: 東京農工大学名誉教授 佐藤勝昭 先生へ
初めまして、お忙しい中メールで失礼したします。
横浜国立大学大学院 修士1年 齋藤 と申します.
現在ナノ粒子の焼結による接合材の研究をしております。
金属の酸化について質問させてください。
金属が酸化すると、一般的にヤング率や破断応力は上がると思いますが、これは何故でしょうか?(Al→Al2O3など)
最終的には、解析の物性値として、ある程度物性を見積もりたのですが,
金属が酸化した場合どの程度ヤング率等(機械的性質)が変化するかわかりません。
(金属の価数との関係も)もしわかることがありましたら、ご教授願います。
------------------------------------------------------------------------------------------------
Date : Tue, 26 Nov 2013 18:49:02 +0900
A1: 齊藤君.佐藤勝昭です。
金属の結晶は原子が金属結合で結び付いています。
金属結合というのは、金属を構成する原子の持つ電子が、自由電子となって結晶全体にひろがり、 この電子の海に原子核が規則的に並んで浮んでいる状態です。
金属が酸化すると、金属は陽イオンになり、酸素のマイナスイオンとの間に静電的な力が働いて結合します。
このような結合をイオン結合といいます。金属結合に比べて、イオン結合は非常に強いので弾性係数が大きいのです。
実際の金属酸化物では、金属の電子の一部と酸素の電子の一部が共有結合で結び付いています。共有結合も強い結合なの で、弾性係数が大きいのです。このように酸化した金属はもとの金属とは全く異なった物質になったと考えるべきです。
------------------------------------------------------------------------------------------------
Date: Thu, 28 Nov 2013 12:33:28 +0900
Q2: 東京農工大学名誉教授 佐藤勝昭 先生
お忙しい中ありがとうございました。
酸化により電子が捕らわれることで、結合の種類が変わり、 結合が強くなる分、延性・展性などの性質を示さなくなるのですね。
結合エネルギーについて調べてみたのですが、 金属-酸素間の結合エネルギーが見つけられませんでした。
なにかオススメの参考文献はないでしょうか??
また、結合エネルギーと弾性係数の間にはどのような関係があるのでしょうか?
勉強不足で申し訳ないのですが、もしわかることがありましたら、ご教授願います。
------------------------------------------------------------------------------------------------
Date: Thu, 28 Nov 2013 15:26:54 +0900
A2: 齊藤君、佐藤勝昭です。
原子間の結合エネルギーを推定するには、heat of formation ΔHf(生成熱)を使う ことができます。イオン性のみを仮定してΔHfを計算しても、酸化物ではイオン性と共 有性を持っているので、実験値をよく説明できないようです。
古い文献ですが、例えば
Calculation of bond distances and heats of formation for BeO, MgO, SiO2, TiO2, FeO, and ZnO using the ionic model: American Mineralogist, Volume 65, pages 163-173, I9B0 をお読みください。
この文献では、イオン性として計算した値と実験で求めた値の違いを共有性としています。
機械的性質との関係ですが、生成熱ΔHfが大きいもの程、体積弾性率が大きくなるというだいたいの傾向はあります。上の論文の表からそれぞれの実験値を引っ張り出して 見ますと
| 物質名 | 生成熱(kcal/mol) | 体積弾性率(1011Pa) |
|---|---|---|
| BeO | -142 | 2.20 |
| MgO | -143 | 1.62 |
| ZnO | -83 | 1.39 |
| FeO | -170 | 1.74 |
-------------------------------------------------------------------------------------------------
Date: Thu, 28 Nov 2013 15:39:20 +0900
AA: 佐藤先生へ
結合エネルギーだけから、考えていくのは難しそうなので、何か別の観点も組み合わせて考えられないか、 教授と相談してみます。
ご親切にありがとうございました。
-------------------------------------------------------------------------------------------------
1312. 太陽光線のじりじり感について
Date : Thu, 28 Nov 2013 20:41:20 +0900Q: 佐藤勝昭 先生
初めてメールさせて頂きます。 S社(化学系)に勤務しておりますNと申します。
先生のHPを拝見させて頂き、非常に広範囲の質問へのご回答をされており非常に参考にさせて頂いております。
小職ですが、現在の業務が省エネ関連の材料開発を行っています。
色々と調べると、例えば建材用途の窓フィルムやコーティング剤の省エネ効果を謳っているHPや文書を多く見かけるのですが、その中で気になる点がありご質問させて頂きました。
それは、「じりじり感」という表現です。これに関して質問させて頂きたく。
感覚的に、じりじり感という物は、体感できイメージ出来るのですが、実際の定量的な意味合いではどのような物になるのでしょうか?また、定量的な評価は可能なのでしょうか?
先生のコメントも拝見致しましたが、現状の先生のご意見を伺えますと幸いです。
以上、宜しくお願い致します。
--------------------------------------------------------------------------------------------------
Date : Thu, 28 Nov 2013 23:48:51 +0900
A: N様、佐藤勝昭です。
じりじり感については、旭硝子の尾関さんが雑誌(NEW GLASS 18 68 (2003))に大変よい解説を書いておられます。
この解説によれば中赤外(この解説では1200-2100nmくらいをさしているらしい)がじりじり感のもとになっているようです。
定量的には、皮膚温度の上昇をサーモグラフィなんかで測定するほかかないでしょうね。
1313. パーマロイの水素焼鈍
Date : Mon, 2 Dec 2013 19:32:41Q: M*社の田中と申します。物性Q&Aをみて質問しました。会社名は非公表でお願いします!
質問は、
パーマロイの透磁率を高めるため焼鈍をしますが、このとき水素の雰囲気で行うようです。
これが、例えば水素と窒素の混合ガスではいけないのでしょうか?
弊社は金属加工の会社でこの辺の所は良く分かりません。教えて頂けませんでしょうか?
近くの熱処理屋さんでは混合ガスなら処理できるといわれているのですが、取引先の資料では水素ガスの雰囲気と書いてあります。
---------------------------------------------------------------------------------------------------
 Date : Mon, 2 Dec 2013 22:03:17 +0900
Date : Mon, 2 Dec 2013 22:03:17 +0900 A: 田中様、佐藤勝昭です。
パーマロイの焼鈍は高純度の水素中で行う必要があります。
FeとNは添付の相図のように反応してFe4Nなどの窒化物を作るからです。
通常、露点-40℃以下でN2含有量50ppm以下の高純度水素中で焼鈍するとされています。
水素焼鈍のやり方で磁気的性質の改善の様子は大いに異なります。
NEOMAX社のPermalloyのサイトを参照してください。
---------------------------------------------------------------------------------------------------
Date : Wed, 4 Dec 2013 10:42:39 +0900
AA: 佐藤先生。有難うございます。
参考にさせていただきます!
弊社は大阪です。近くで熱処理出来るところを探しています。
これが、クリヤー出来ればパーマロイの加工の仕事が取れるかもしれません。
田中
----------------------------------------------------------------------------------------------------
1314. 無磁場で生じる円二色性
Date : Wed, 4 Dec 2013 14:32:00 +0900Q: 佐藤先生、ご無沙汰しております。K社のMです。今、合成専門の人とある光学活性を示す有機化合物を対象とする材料開発をやっています。
これがうまく合成できたかどうかを確認するためには円偏光二色性(CD)スペクトルをとったらいいのではないかと思い、 昨日からCDの勉強をしております。
それで先生の「光と磁気」(2001年版)を読んでいて教えていただきたいことが出てきました。
p8に「酒石酸の水溶液などでは右円偏光と左円偏光とに対して吸光度が違うという現象がある。これを二色性という」と書かれています。
これを読んでいぶかしく思ったのですが、図2.4のような実験では試料には磁場がかけておらず、酒石酸自体も磁性体ではありません(反磁性体ではありますが)。
このようなものでも円二色性が現れるのは、光の中の磁界Hと酒石酸の中の電子との相互作用(反磁性磁化率を介する)のせいでしょうか。
つまり、p29の(3.12)のεxy の中には光の磁界Hと反磁性磁化率とが含まれているのでしょうか。
もしそうだとするとそのεxyの具体式はp62の(4.6)において直流磁界Bを高周波磁場Bに置き換えて解けば得られるのでしょうか。
(HPの「1170 複素屈折率と磁気光学」に関連の質問があります)p.s 図2.4の試料は「右旋酒石酸のクロムナトリウム塩」と書いてありますが「右旋酒石酸 のカリムナトリウム塩」の間違いではありませんか?いわゆるロッシェル塩のことです。
-----------------------------------------------------------------------------------------------------
Date : Thu, 5 Dec 2013 00:31:36 +0900
A: M様、佐藤勝昭です。
自然活性(旋光性と円二色性)は、結晶構造または分子構造によって生じるもので、磁性とは全く無関係です。水晶にも旋光性がありますが、これは、結晶構造的に原子の 配列にらせんがあるからです。
化学の方ではキラル(不斉)分子と呼ばれる構造によります。(野依良治先生のノーベル賞受賞の対象になったのは「不斉配位子をもつ金属錯体を触媒に用いて、 不斉分子の合成を行ったこと」とされます)
二色性が現れるのは、らせん構造のために右円偏光と左円偏光に対する光学遷移(光の吸収)が異なるという選択則のためです。磁性は全く関係ありません。
図2.4のキャプション、ご指摘ありがとうございます。「右旋酒石酸のカリウムナトリウム塩」の間違いです。
-----------------------------------------------------------------------------------------------------
Date : Thu, 05 Dec 2013 20:15:08 +0900
AA: 佐藤先生
お返事ありがとうございます。
> 水晶にも旋光性がありますが、これは、結晶構造的に原子の配列にらせんがあるからです。
昔、院生の時、研究室に鉱物の薄片試料がありましたが、その中に水晶もありまして、これを偏光顕微鏡でのぞいて旋光性の観察をしました。
> 化学の方ではキラル(不斉)分子と呼ばれる構造によります。
まさに今やっているのはキラル分子です。
> 二色性が現れるのは、らせん構造のために右円偏光と左円偏光に対する光学遷移(光>の吸収)が異なるという選択則のためです。磁性は全く関係ありません。
なるほど。私も昔、時間を含むシュレディンガー方程式から遷移確率を求める式をフォローしたことがありますが、電子双極子遷移の中の振動子強度がどうなるかなのですね、本質は。
化学の実験ではよく溶液の可視紫外吸収スペクトルを測っていて選択則の議論も出ますが、この議論では偏光を入射することは前提にはなかったと思います(遷移金属錯体の本では円偏光二色性が出ますが)。
それが偏光を使うとどうなるかを考えればいいのだと理解しました。それで「光と磁気」の本のp68からp71を勉強してみます。
------------------------------------------------------------------------------------------------------
1315. スピン注入のメカニズム
Date : Thu, 05 Dec 2013 14:19:51 +0900Q: 佐藤勝昭先生
H*大学大学院に所属しておりますM2のT*と申します。(webアップ時は匿名でお願い致します。)
HPを拝見させていただき、ご連絡致しております。
私は半導体工学を専攻していますが、材料を広く勉強したいと思い、現在は磁性体に関して独学しております。
このたびは、私自身で文献を色々とあさってみましたが、理解のできる詳しい説明の記載されているものがみつからず、 連絡差し上げた次第でございます。
以下、質問です。
===================================================================
強磁性体と非磁性体を接続させた系について考えます。
強磁性体から非磁性体にスピンを注入した場合、非磁性体内に非平衡スピンが蓄積されます。
蓄積された非平衡スピンは“バックフロー”と呼ばれる現象により、その大部分が強磁性体内に逆戻りし、結果的にスピンの注入効率は低くなります。
これに関して、
質問①:
ある文献によると“バックフローが生じる原因は強磁性体がスピン緩和の大きな材料であるため。”と記載されておりました。
“スピン緩和が大きい”とは具体的にどういうことなのでしょうか。
また、どうしてスピン緩和が大きいとスピンを吸収するのでしょうか。
質問②:
強磁性体と非磁性体の伝導度のミスマッチが大きいと、スピン注入の効率が非常に悪くなります。これを回避するために間に障壁を挟むとよい ということですが、これはどうしてでしょうか。
また、障壁を挟むことによってバックフローの影響はどうなるのでしょうか。
===================================================================
以上です。
お忙しい中恐縮ではございますが、ご返答よろしくお願い致します。
----------------------------------------------------------------------------------------------------
Date : Fri, 6 Dec 2013 00:50:50 +0900
A: T様、佐藤勝昭です。
私はスピン注入の詳細については、自信がないので、半導体へのスピン注入の研究をしている九大の浜屋宏平准教授にお尋ねしました。
以下、浜屋さんの回答に基づいてお答えします。
質問1:
ご質問の箇所での「スピン緩和」ですが、主にスピン伝導の拡散距離 (スピン拡散長)に関する記述と思われます。
一般的に、強磁性体と非磁性体の「スピン拡散長」を比較すると、強磁性体= 数nm、非磁性隊 = 数μmという程、大きな違いがあります。
つまり、強磁性体では非平衡スピン蓄積 (=スピン流)の拡散距離が短く、すぐに平衡状態に戻ってしまうことを、「スピン緩和が大きい」と表現していると思われます。
「スピン緩和が大きいとスピンを吸収する」理由ですが、「非平衡スピン蓄積 (=スピン流)」と記述されていますように、非平衡状態は平衡状態へ戻ろうとします。
つまり、上記の解釈に有るように、平衡状態に戻してくれる(スピン緩和の大きな)強磁性体に、非平衡スピン蓄積(=スピン流)は吸収されやすいということになります。
質問2:
強磁性体/非磁性体界面に障壁層を挟むと、接合界面で滑らかに繋がっていた電気化学ポテンシャルが途切れてしまうため、伝導度ミスマッチを考える必要がなくなります。
つまり、電界アシストなどで一旦、強制的に非磁性体中にスピン注入が実現すると、非平衡スピン蓄積(=スピン流)は非磁性体中にしか拡散することができません。
これは、絶縁障壁層の伝導度が極めて低く、スピン流の拡散を許さないからです。
結果として、絶縁障壁層の向こう側に存在する強磁性体には、ほとんどスピンが拡散することはなくなります。これが、バックフローの抑制です。
伝導度ミスマッチの別の表現で、「スピン抵抗差」という概念が有りますので、そちらでも簡単に説明します。
一般的に「スピン抵抗」は、強磁性体 < 非磁性体 < 絶縁体です。一旦、非磁性体中にスピン注入が実現すると、
非磁性体よりもスピン抵抗の大きな絶縁障壁層の方にはスピン拡散が許されず非磁性体内のみのスピン拡散が主となります。
つまり、絶縁障壁層はスピン抵抗の最も小さな強磁性体へのスピン拡散をほとんど許しません。
結果として、スピン流のバックフローは抑制されることになります。
-------------------------------------------------------------------------------------------------
Date : Fri, 06 Dec 2013 20:47:00 +0900
AA: 佐藤勝昭先生、H大のTです。
メール拝読致しました。早急のご返答、誠にありがとうございました。
九州大学の浜屋先生は私自身面識はございませんが、磁性体(スピン)の勉強を始めて、何度か著書やHPを拝見したことがございます。
私のために連絡をとっていただき、本当に感謝しております。回答いただいた浜屋先生にも、よろしくお伝え下さい。
「スピン緩和」に関する回答、また「スピン抵抗差」の概念等非常に勉強になりました。さらに掘り下げて勉強してみようと思います。
以上です。
--------------------------------------------------------------------------------------------------
1316. セラミクスのスパッタ成膜速度とガス圧の関係
Date : Thu, 19 Dec 2013 16:45:48 +0900 Q: 初めまして.T*大学大学院1年のT*と申します.
Q: 初めまして.T*大学大学院1年のT*と申します.スパッタリングの分野について質問させてください.
実験装置にRFマグネトロンスパッタリング(チャンバー内容積 : 約32×10^-3 [m3]),
ターゲットをイットリア安定化ジルコニア,基板をSi(001),
フローガスをAr,RFパワー200Wで実験を行っています.
今回質問しますのは,成膜速度の問題です.
 一般的にチャンバー内圧力を増加させると平均自由行程が短くなるため成膜速度が
一般的にチャンバー内圧力を増加させると平均自由行程が短くなるため成膜速度が下がるというのが周知の事実です.
私の実験では,Arガス流入量を増加させ(20→100sccm)て実験を行っています.
チャンバー内圧力を増加(100sccm)させた場合成膜速度が下がるどころか少ない
(20sccm)場合と比べて増加しました.
ターゲット-基板の入射角度がon-axisではあまり影響はないのですが,ターゲット
-基板距離と入射か角度を持たせた場合では膜厚が約2倍に増加しました.
たしかに,不活性ガスの流入量が増加すればそれだけターゲットをたたくAr+の
量が増え,スパッタ粒子の飛来する量が増えたためだと考えれば納得がいくので
すが平均自由行程(λ)は公式よりチャンバー内圧力が増加すれば短くなるはず
が,この結果だけから判断すると長くなったという結果になるのですか?
------------------------------------------------------------------------------------------------
Date : Sun, 22 Dec 2013 11:13:03 +0900
A: T君、佐藤勝昭です。
お返事が遅くなりました。私は、真空工学の専門家ではないので、一般論でお答えします。
ご質問は、「YSZのマグネトロンスパッタ成膜において、Arガス流量(従ってガス圧)を変えたときに、平均自由行程λが減少するはずなのになぜ成膜速度が増加するか」ということですね。
成膜圧力が0.2Paであればλ~3cm, 1.1Paであればλ~1cmとなりますが、ポンプの排気速度が大きい場合、ターゲット・基板間付近の実際の圧力は、もっと低いのではないでしょうか?
例えば、もし0.02Paであれば、λ=34cmにもなりますから、ガス圧を変えてもλがターゲット・基板間のサイズより十分長いため、拡散律速(平均自由行程律速)にはならず、供給律速になって、ガス流量とともに成膜速度が増加します。
On-axisであまり変化がなかったと言うことは、この条件下では圧力が高いため、実際の平均自由行程λがターゲット・基板間距離Lとほぼ等しく、拡散と供給が釣り合っているのでしょう。Off-axisにするとターゲット・基板間の圧力はより低くなるので、λ>>Lとなり、もはや拡散律速にならず、供給律速になるのではないでしょうか?
-----------------------------------------------------------------------------------------------
Date : Sun, 22 Dec 2013 17:16:58 +0900
A': 追伸、T君、佐藤勝昭です。
Facebookにアップしてコメントを求めたたら、東理大の杉山先生から
「T-S間が10cm程度の小型(ターゲットの大きさが書いてありませんが)RFスパッタ装置の場合、
Arプラズマに起因する基板へのダメージや、エロージョンと基板取り付け位置の兼ね合いで、
デポレートや膜質は平均自由行程以外の要因に左右されると思います。」
というコメントをもらいました。参考にしてください。
-------------------------------------------------------------------------------------------------
Date : Mon, 23 Dec 2013 08:22:38 +0900
A":追追伸、T君、佐藤勝昭です。
信州大の森迫先生から、Facebookを通じて、次のようなコメントを頂きましたので、参考にしてください。
「多分、数mTorrから圧力をあげたんだろうと考えてます。RFスパッタでフェライト薄膜を作製した経験からですが、同様にレートが増加しました。スパッタに寄与するイオンが増加したからだろうと思ってました。幾何学的な形状にも依存しますが、10mTorrを超えるとレートは減少します。衝突回数が増えるからでしょう。そして組成(私の場合バリウムと鉄)も変化してました。」
-------------------------------------------------------------------------------------------------
Date : Tue, 24 Dec 2013 08:15:07 +0900
AA: 佐藤先生、御回答感謝します。そして、facebookを通じてヒントを下さった杉山 先生と森迫先生にも感謝します。
確かに、佐藤先生のおっしゃるように不活性ガスの流入量を増加させると、ター ゲットからの放電の明るさは強まっていたため、供給律速は強まったと思われま す。杉山先生のおっしゃるように基板へのダメージが私も少し気になっていたた めこれからは考慮していこうと思います。そして、森迫先生の意見に関して、私 も同じ考えです。私の実験でも組成が変化している傾向が確認できました。
お三方の貴重なアドバイスをもとにこれからも実験に取り組んでいこうと思って います。ありがとうございました。
-------------------------------------------------------------------------------------------------
1317. 炎色反応
Date : Tue, 24 Dec 2013 11:25:18 +0900Q: 佐藤先生
いつも物性なんでもQ&Aを拝見させていただいております。
中学生の息子と炎の発光について話をしていて、自分自身メカニズムが理解できていないことが分かりまして、先生に質問させて頂きました。
炎色反応の発光は原子が励起状態から基底状態に戻る遷移による発光と言われます。この励起状態とはどんな状態なのか、が質問の主旨です。
しばしば見かける説明に、炎色反応を起こしている金属原子はプラズマになっており、電離したイオンと電子が再結合する際の発光というものがあります。
しかし一方で、例えばナトリウムの炎色反応の発光の590nm線は最外殻の3s電子が3p軌道に励起されて、再び3s軌道に戻る遷移に相当する筈で、この場合発光は単に原子内の電子の遷移によるもので、ナトリウム原子は電離しているわけではないと理解しています。
実際はどういった状態の遷移が起こっているのか、ご教示いただけると幸いです。
所属: 日鐵住金株式会社
氏名: 出合博之
-------------------------------------------------------------------------------------------------
Date : Wed, 25 Dec 2013 00:28:46 +0900
A: 出合様、佐藤勝昭です。
第1イオン化エネルギーを理科年表で見ますとLi 5.392eV, Na 5.139eV, K 4.34eV, Sr 5.696eVと、いずれも紫外域ですから、「電離したイオンと電子が再結合する際の発光」は目に見えません。
炎色反応で見えている光学遷移は原子の励起状態から基底状態への電子遷移によると考えてよいと思います。
ただ、電離状態の再結合による紫外線を原子が再吸収して励起状態になり、ここから基底状態に遷移するパスもあるでしょう。
これを「炎色反応を起こしている金属原子はプラズマになっており、電離したイオンと電子が再結合する際の発光」と表現したのではないかと存じます。
--------------------------------------------------------------------------------------------------
Wed, 25 Dec 2013 13:26:24 +0900
AA: 佐藤先生
御回答いただきまして、有難うございます。
大変すっきりいたしました。
身近な現象でも、正しく理解していないことがしばしばあるのですが、今回はその典型でした。
出合
--------------------------------------------------------------------------------------------------
1318. 強磁性体単結晶と多結晶の磁化の違い
Date : Fri, 10 Jan 2014 11:34:11 +0900Q: 佐藤勝昭教授
K*大学修士1年のT*と申します。物理学を専攻しております。
いつも佐藤教授のQ&Aコーナーを興味深く拝見しております。
名前を掲載される際は匿名でお願いいたします。
磁性に関して質問が2点あり、質問させて頂きます。
1. 強磁性体の多結晶と単結晶の磁化の値についてです。
例えばC軸が磁化容易方向である磁気異方性をもつ単結晶の強磁性体に磁場(仮に5Tとします)をかけて温度を下げていき安定した値と、
同じ物質の多結晶で同様に行った場合では安定した際の磁化の値は異なるかと思います。(値は単位molあたりのです)
同じ物質でも単結晶のほうが多結晶よりも磁化の値は大きいはずですが、一般的に何倍ほど大きくなると考えるべきでしょうか?
またその理由は何故でしょうか?
2. 同じ物質の単結晶、多結晶のキュリーワイス定数についてです。
上記と同じ磁気異方性をもつ単結晶のキュリーワイス定数が仮に1であったらとしたら理論上では多結晶のキュリーワイス定数は
どれくらいになると見積もるべきでしょうか?
お忙しい中恐縮ではございますが、どうぞよろしくお願い致します。
-----------------------------------------------------------------------------------------------------
Date : Sat, 11 Jan 2014 01:44:03 +0900
A: T君、佐藤勝昭です。
(1)異方性定数Kuが大きな磁性体多結晶の磁化特性についてのご質問
もし、その強磁性体が単磁区微粒子から構成されているとしましょう。
その微粒子の異方性磁界Hkは2Ku/Msで表されます。各微粒子の結晶軸は、バラバラな方向を向いていますが、
Hkより十分大きな外部磁界を加えれば、最後は磁化方向が磁化容易方向からずれ、磁気異方性エネルギーに
逆らいながら回転し飽和に達します。
あなたが加えた5Tという磁界がHkより大きければ、多結晶でも単結晶でも飽和磁化の大きさは原理的に同じはずです。
もし印加磁界5TがHkより小さければ、各微粒子の磁化はそろわないので、磁性体全体として飽和しません。
このとき多結晶の磁化は単結晶の磁化より小さくなりますが、何%ということはできません。
もう一つ考慮すべきは、反磁界のことです。多結晶体を構成する結晶粒の形状が針状は、平板状か、球形かによって、
反磁界が異なりますから、場合によっては、実効磁界は印加磁界よりかなりばらついている可能性もあります。
このようなときには、なかなか飽和しない可能性があります。
(2) 異方性をもつ多結晶強磁性体のキュリーワイス定数
キュリー温度以上の常磁性相でのキュリーワイスの法則は、自発磁化が失われていることが前提となっています。
自発磁化がないのですから、磁化容易軸の概念もないはずです。従って、多結晶でも単結晶でも原理的には、
キュリーワイス定数は変化がないはずです。
----------------------------------------------------------------------------------------------------
Date : Sat, 11 Jan 2014 11:37:05 +0900
AA: 佐藤教授
ご解答どうもありがとうございます。
大変すっきりしました。貴重なご意見を頂きありがとうございました。
----------------------------------------------------------------------------------------------------
1319. アモルファス金属について
Date: Thu, 27 Feb 2014 17:19:11 +0900Q: 佐藤勝昭先生、はじめまして。K*社製造部のI*と申します。
アモルファス金属について調べて漂流しているうちに、こちらの宝島のようなHP「物性なんでもQ&A」に流れ着きました。
早速ですが質問です。アモルファス金属とは非晶質の金属のことで、原子配列が無秩序になっているそうですが、
① 有機高分子鎖が絡み合いや立体構造的に結晶化しにくいのは納得しやすいのですが、(私が考えるに)鎖状ではない金属原子が結晶化前に凍結できてしまうのはどういった理由によるのでしょうか。 単に金属が重くて運動にはたくさんのエネルギーが必要だからでしょうか。
② 金属結晶における電子(非局在化電子)はアモルファス金属ではどうなってしまっているのでしょうか。
導電性、熱伝導性、金属光沢に変化はあるのでしょうか。
③ アモルファス金属を室温~1000℃まで変化させた場合、見た目・原子配列に変化はあるのでしょうか。また、金属ガラスではどうでしょうか。
④ アモルファス金属を油圧プレスローラで圧延する、ナイフで切りつけるなどの機械的作用をした場合、見た目・原子配列の点でどのような応答をするでしょうか。
普通の結晶金属と顕著な違いはありますか。
⑤ 例えばチェーンソーで切断するなど、摩擦熱作用と物理作用が複合した場合は見た目・原子配列の点でどのような応答をするでしょうか。火花が散ったり切断面が焼けたりするのでしょうか。
不躾にもたくさん質問してしまいました。お忙しいところ申し訳ありませんが、ご教授いただければ幸いに存じます。
--------------------------------------------------------------------------------------------------
Date: Fri, 28 Feb 2014 00:10:49 +0900
A: I様、佐藤勝昭です。
アモルファス金属についての広範なご質問なので、全部にきちんとお答えできるか自信はありませんが、私の知っている範囲でお答えします。
(1)分子鎖や絡み合いがないのにアモルファスになる理由:
アモルファス金属は、Fe, Coなどの金属原子とSiやBなどのglass forming atomとから成り立っています。
CD-RWに使われている材料はAg-In-Sb-Teですが、金属Ag, In, Sbと非金属Teとから成り立っています。
融点以上に加熱すると融解します。融液においては原子の配置は不規則状態になっています。
この融液を徐冷すると原子が移動して規則的な原子配置になり「結晶」となります。一方、この融液を急冷すると、短時間に原子が移動して長距離の秩序構造を採ることができず、アモルファス状態になります。
アモルファス金属は、いわば、液体状態における原子配置がそのまま凍結したようなものです。
Ag-In-Sb-Teのように大きさの異なるいろんな玉をきちんと並べるのは困難なので非晶質になりやすいです。
理論的には、硬球乱雑稠密充填モデル(random close packing of hard spheres)でよく説明されます。
非晶質状態にあるものを結晶化温度以上に保つと結晶化が進みます。CD-RWでは、結晶相と非晶質相の相変化を用いて、記録・消去を行っています。
(2)非局在化電子による物性はアモルファス金属でどうなるか
アモルファスにおいては周期構造がないので、周期構造に基づくバンド構造は大きな変化を受けますが、バンドギャップが開くわけではないので、フェルミ準位は伝導帯内にあり金属伝導性はかわりません。
一例として溶融金属急冷法で作成したアモルファスPd80Si20を取り上げますと、結晶の場合に比べて1桁以上抵抗率が高くなっています。温度を上昇していくと普通の金属と同様に抵抗率が増加しますが、結晶化温度350℃を超えたとたん、抵抗率は急落して、結晶相の小さな抵抗率の値になります。
アモルファスにおけるこの抵抗率の上昇はキャリア密度の変化によるのではなく、ランダム散乱によると考えられます。キャリア密度が変わらないので、自由電子乃Drude則による反射率はあまり変化がないのではないでしょうか。熱伝導率は電気伝導率に比例するので、アモルファスでは結晶相より低いと思います。
(3)温度上昇にともなう見た目・原子配列の変化
温度上昇がゆっくりだと、徐々に結晶化が進むと思います。見た目の変化はあまりないと思います。
(4)(5)圧延・切断などの機械的処理で何が起きるか
やったことがないので、わかりませんが、圧延や切断にともなって温度上昇があれば結晶化が促進されると思います。
------------------------------------------------------------------------------------------------
Date: Mon, 3 Mar 2014 09:32:29 +0900
AA; 佐藤先生、Iです。
迅速で丁寧な回答をしてくださったのに御礼が遅くなりまして申し訳ありません。
ご回答の中にありました専門用語を調べていて遅くなってしまいました。
知人がアモルファス金属を加工する機会があり、仕事中誤って加工物を弾き飛ばしてしまったそうです。
知人は普段ステンレスや鉄鋼を扱うことが多いのですが、「見た目はステンレスに似ているのに、床に激突してもキズがつかず非常に驚いた」という話を聞いて興味が湧き、今回の質問に至った次第です。
知人にアモルファス金属の強さの根拠について説明してみせたかったのですが、私がアモルファスを語るには基礎的な部分の理解がまだまだ足りないようです。
先生のお言葉でいくつか探索するべきルートが拓けたのでそちらを勉強してこようと思います。
壁に当たったときはまた先生を頼ってしまうかもしれません。そのときはどうかよろしくお願い致します。
------------------------------------------------------------------------------------------------
1320. 銀950の熱伝導率と熱膨張係数
Date: Wed, 16 Apr 2014 12:03:29 +0900Q: 佐藤先生, お世話になります。D社の山田です。
HPを見て問い合わせをしております。
Ag(銀)950というのがありますが、この材料の熱伝導率と熱膨張係数を知りたく思っています。
放熱板などへの適用を検討しています。
文献などの紹介でも結構です。
宜しくお願いします。
-----------------------------------------------------------------------------------------------
Date: Wed, 16 Apr 2014 13:59:15 +0900
A: 山田様,佐藤勝昭です。
申しわけありませんが、私は、950銀(Ag95Cu5)合金の熱伝導率/熱膨張係数のデータを持ちあわせません。
・丸善の金属データブック(2008年)によれば、AgにCuを5at%添加したときの電気抵抗率は純粋のAgより25%くらい高いようです。
ヴィーデマン=フランツ則 によれば、金属の熱伝導率は電気伝導率に比例するので,純銀より25%程度低いと推察されます。
・Ag-Cu合金の線膨張係数については手がかりが全くありません。5%くらいのCuの固溶では格子定数も殆ど変化がありませんから、 950銀の線膨張係数は銀の値を使っておいてよいのではないでしょうか.
-----------------------------------------------------------------------------------------------
Date: Wed, 16 Apr 2014 14:21:57 +0900
AA: 佐藤先生, お世話になります。
早速のご回答、誠に有難うございます。
助かりました。
-----------------------------------------------------------------------------------------------
1321. 金属の斜め入射反射光の色味
Date: Thu, 24 Apr 2014 11:33:44 +0000Q: 佐藤先生
始めまして、K社のBと申します。HPを見て、問い合わせをさせていただきました。
お手数ですが、下記ご回答いただければ幸いです。
(大変恐縮ですが、Webで公開する場合には社名・氏名ともに匿名でお願い致します)
金属の反射メカニズム について2点、質問をさせていただきます。
(1) 金属に対する、光の斜め入射に関する件
「金属では、光の入射角度が垂直から徐々に浅くなるにつれて、P偏光の反射率はいったん減少後に増加して (誘電体におけるブリュースタ角の考え方)S偏光の反射率は単調増加する」という認識ですが、そのときの色味はどうなるのでしょうか?
机上検証では、
同様に、入射角度が垂直から徐々に浅くなるにつれて、
P偏光は 常に変わらず金属の色味(金属光沢) が見えて (金であれば金色)
S偏光は 金属光沢が徐々に薄れて、光源色が見えるようになる
という感触を得ています。
ただし、
金属の反射は、自由電子の波長選択性をもった振動が関連しているため、
金属の色味(金属光沢)を持つという認識であり、
「S偏光の反射で光源色が見えるようになる(金属光沢がなくなる)」のには違和感を持っております。
(2) 凹凸のある金属が白っぽく見える件
・紙やすりで荒らして、凹凸のある銅盤 (数10マイクロメートルオーダの凹凸)
・バフ研磨して、表面が滑らかな銅盤
これらを比較すると、前者の、凹凸のある方が白っぽく見えます。
金属の「拡散反射」も、結局は自由電子が関連する「正反射の集まり」と考えているため、
凹凸があっても、変わらずに金属の色味(銅色)が見えるかと思ったのですが、そうは見えません。
これは何故なのでしょうか?
推測ですが、上記(1)とも関連しているのではないでしょうか。
目に見える光は、斜め入射光の集まりであり、
斜め入射だと、S偏光では徐々に光源色が見えるようになり、結果として全体的に白っぽく見えると考えております。
これらの仮説を検証する手立てがなく、恥ずかしながら社内にノウハウもございません。
お忙しいところ恐縮ですが、ご教示いただければ幸いです。
以上、よろしくお願い致します。
-------------------------------------------------------------------------------------
Date: Mon, 28 Apr 2014 01:14:22 +0900
A: B様、佐藤勝昭です。
お返事が大変遅くなりましたことをお詫びします。
これまで、斜め入射反射において、スペクトルのことまで考えていなかったので、実際にどうなるかを計算してみました。
 計算式は、光の反射メカニズムの拙文を参照して下さい。
計算式は、光の反射メカニズムの拙文を参照して下さい。Cuの反射スペクトル、計算結果の図をご覧下さい。
緑線はp偏光、青線はs偏光、赤線は平均値(無偏光)です。
p偏光のスペクトルは、600nmより短波長の反射率が入射角と共にどんどん低下します。
この結果偏光子を使ってp偏光だけを見ると、だんだんはっきりした赤になっていきます。
これに対し、s偏光のスペクトルは入射角が増加すると共に、600nm以下の波長の反射率が 高くなるので、偏光子でs偏光だけをみると銀色っぽくなります。いわば普通の鏡に近くなります。
無偏光の場合も、入射角とともに、短波長の反射率が高くなって、白っぽい赤色になるはずです。
金属光沢がなくなるのは別の理由によると思います。それは、表面の凹凸による散乱が 斜め入射ほど大きく影響するからです。また、凹凸が大きい程、入射角が大きな反射光の 成分の影響が強くなるため、白っぽくなるのです。
-------------------------------------------------------------------------------------
Date: Mon, 28 Apr 2014 09:23:38 +0000
Q2: 佐藤先生
お世話になります、K社のBです。
ご連絡ありがとうございます。
私の周りの者も含め、先生の迅速なご対応に、ただただ驚き感謝している次第です。
さて、ご返答いただいた件ですが、今回新たに反射スペクトルを計算いただいたようで誠にありがとうございます。
確かに、銅のP偏光は入射角とともに赤みを増していくように見えます。
机上実験の感触通りの、技術的な裏づけを示していただき、また、これまで手当たり次第に得ていた知識が、すっと繋がったようで、大変すっきり致しました。
ちなみに、計算式としては、紹介いただいたPDFの(33)式で合っていますでしょうか。よろしくお願いします。
-------------------------------------------------------------------------------------
Date: Mon, 28 Apr 2014 20:06:14 +0900
A2: B様、佐藤勝昭です。
確かに資料の式(33)で計算しました。
-------------------------------------------------------------------------------------
Date: Thu, 8 May 2014 02:49:06 +0000
AA:佐藤先生
お世話になります、K社Bです。
ご連絡遅れ、申し訳ございません。
ご回答ありがとうございました。
今後も、不明点あれば質問させていただければ幸いです。
以上、取り急ぎになりますが御礼のみにて失礼致します。
--------------------------------------------------------------------------------------
1322. Mgドープ窒化ガリウムに関する質問
Date: Tue, 13 May 2014 16:09:24 +0900Q1: 佐藤勝昭 先生
先生の「物性なんでもQ&A」を拝見し、メールさせて頂きました。
私はK社のS*と申します。GaN関係の開発を行っております。
私自身は化合物半導体のエンジニアです。ちなみにこの道10年ほどです。
常々佐藤先生のHP、講義資料などを拝見し、いろいろ勉強させて頂いております。
今先生のコンテンツを含め、色々なチャネルを活用してもどうしても解けない問題に 直面しており、先生のQ&Aのコーナーにて、質問させて頂こうと思った次第です。
お時間頂けましたら幸いです。
質問はMgドープGaNで見られます、奇妙な現象についてです。
【MgドープGaNに現れる不規則パターン】
現在当方ではMgドープGaNを調べております。調べる際に標準としているエピ構造は、c面サファイア上のc面GaNのヘテロエピで、2~3um厚のu-GaN層の上に250~500nm 厚のMgドープGaNというものになります(条件により膜厚が異なりますので幅を持たせて記載しました)。成長方法はMOCVD法で、自公転式の反応炉を用いています。
我々の条件でMgドープGaNを成長すると、表面に不規則形状のパターンが生じることがあり、それが今悩みの種となってます。
パターンは水滴ライクの小さい領域から成っていたり(図1)、比較的広い領域から形成されていたり(図2)、円弧を描く筋状だったり(図3)と、いろいろな様相を示します。
3番目の円弧状パターンは不規則とは言えないかもしれません。基板研磨でこのようなパターンが出来そうなので、今のところ基板に起因するパターンを引き継いでいるのではないかと推測してます。
いずれにしましてもこのパターンは、肉眼及び微分干渉顕微鏡で観察可能で(図1)、微分干渉顕微鏡による観察から、パターンは表面の高低差に起因していることが分かってます。
MOCVD法の成長原理から、結晶そのものに何らかの原因が無ければ、このようなパターンの高低差が生じることは考えにくいと思います。
再現性については、パターン形状はまちまちですが、ある条件下で成長すれば必ずこのパターンは出現します。
 (図1) |
 (図2) |
 (図3) |
 (図4) |
【極性仮説】
現在の我々の予想は、このパターンは極性の違いに起因して生じるのではないかと考えております。
ご存知のようにウルツァイト型結晶であるGaNは、中心対称のない結晶であり、c軸方向に+/-の極性があります。
一方、GaNにMgを高濃度でドープすると、極性が反転するという文献が幾つかあります。ちなみに我々のサンプルでは20乗前後でドープしてますので、高濃度の部類に入ると思います。
また極性により成長速度が異なりますので、これらのことを総合的に判断すると、極性の違いによりパターンが形成されているというのは、合理的な解釈と思っております。
ちなみに極性を同定したいと思っておりますが、設備が無いため今のところ未実施です。
【謎の532nmピーク】
さらに奇妙なことがあります。PLマッピングを取ると、表面パターンに一致するパターンが観測されます(図2)。
スペクトルを参照すると532nmのピーク強度の違いによるコントラストと分かります。つまりパターンを構成する2相のうちの一方は532nmピークが強く、もう一方は弱いということです。
PLの励起光源はYAG1/4波長であり、532nmは丁度その倍です。そのため非線形光学効果がまず最初に浮かびましたが、c面に垂直にレーザー光を照射しているため、これは原理的にはないと考えられます。
【光源に含まれる532nmの反射?】
次に考えましたのは、光源に含まれる532nm光の反射です。あるレーザーの専門家から、YAG1/4波長の光源は幾らかの1/2波長(つまり532nm)を含むということを聞きました。
そこでサファイア基板のみのPLスペクトルを測定してみました。結果、532nmにピークがあり、その強度は約0.6a.u.でした(図4)。サファイアでは532nmの発光も吸収もないと思います。
つまりこのピークは、純粋に光源に含まれる532nm光の反射と考えていいと思います。
サファイアの屈折率(1.77)から反射率を計算すると約8%となりますので、光源を直接ディテクタで測定すると532nmの強度は7.5a.u.となると計算されます。
なお本質と関係ないとは思いますが、532nmピークがやけに幅が広い(528~537nm)のが気になってます。こんなにブロードになるのは普通なのでしょうか?
一方GaNの屈折率はこの波長で約2.4ですので、吸収が無いとすると反射率は約17%になるはずです。従いまして、特殊なことが無ければGaNでは7.5×17%=1.3a.u.程度の強度が観測されるはずです。
【532nm強度が弱すぎる矛盾】
ところが先に述べましたMgドープGaNは、532nmが強いときでもせいぜい0.1a.u.程度であり、予想される強度の10%にも満たないのです。しかも弱いときは532nmピーク強度はほぼゼロです。
つまり反射率が限りなくゼロに近いということになってしまいます。ちなみに通常のu-GaNでも532nmピークは非常に弱く、Mgドープに限った問題ではないようです。
最初532nmの吸収のせいかとも思いましたが、吸収があれば反射率はより高くなる(逆に言えば、特殊なことがない限り吸収がない場合が一番反射率が低い)と思いますので、吸収ではないでしょう。
(この考え正しいでしょうか?)
【ARコート効果?】
次に考えたのは、ARコート効果ですが、GaN/Sapphire界面の反射率はGaN/Air界面の反射率より一桁近く低いため、GaN/Air界面反射をほぼ打ち消すような状況にはなり得ないと結論しました。
【表面粗さ?】
次は表面粗さです。これについては他にデータがあります。我々のPL測定装置では、白色光の薄膜干渉を用いた膜厚測定も可能でして、その際反射率を同時に測定する機能が付いてます。
その反射率の数値は(単位は不明ですが)サファイアで100、普通の鏡面の出ているGaNで230ぐらいを示します。サファイアとGaNの反射率比は2.2ぐらいですので、測定されている反射率の比と調和的です。
そして230の反射率を示すGaNサンプル(つまり十分平滑な表面)でも強い532nmピークが観測されることはありません。
【サンプルの傾き?】
あとはサンプル表面の傾きも考えられますが、膜厚分布の非常に良いサンプルの中心領域を考えますと、GaN表面はサファイア面に対して傾きようがないと思います。このような領域でも強い532nmピークは観測されないですので、傾きのせいでもないでしょう。 【質問1】 以上のように煮詰まってしまいました。まとめますと、サファイアのPLスペクトルから励起光源は比較的強い532nm光を含むことが予想されますが、この光源をGaNに照射したときは532nmの反射光が殆ど観測されない、ということになります。何故観測されないかが第一の質問です。あるいは反射という仮説が正しくないのでしょうか? 【質問2】 第2の質問は、表面パターンと532nm強度との関係です。私どもの極性仮説、及び反射仮説が正しいとすれば、極性により532nmの反射率が異なるということになります。
そのようなことはあり得るのでしょうか?光学的には極性の+/-は関係ないように思うのですが・・・。あるいはこれも極性仮説、反射仮説が正しくないのか?
以上の2点が質問です。何かお分かりになること、私の考察で間違っていることなどがありましたら、何卒ご教授下さい。よろしくお願い致します。
---------------------------------------------------------------------------------------------------------------
Date: Tue, 13 May 2014 16:54:36 +0900
A1: S様,佐藤勝昭です。 メール有り難うございます。たしかに不思議がいっぱいですね。 (1)まず、GaN MOCVD膜のhillockの原因ですが、あなたの推察通り、極性反転領域(Inversion Domain)と考えてよいと思います。
ホモエピにおいてもhillockが観測されており、極性により成長速度が異なることが原因とされています。
たとえば、 J.L. Weyher et al., Morphological and structural characteristics of homoepitaxial GaN grown by metalorganic chemical vapour deposition (MOCVD), J. Cryst. Growth 204 (1999) 419-428
(2)サファイヤで見られる532nm光の反射がGaNをつけたときに帰ってこないのは,GaNの膜厚が1/4波長付近にあって往復で1/2波長となってうち消すためです。
この532nmがYAG励起光に含まれる532nm光かどうかは、励起波長(216nm)のみを透過するフィルタをかませれば,なくなることで確かめられるはずです。
----------------------------------------------------------------------------------------------------------------
Date: Tue, 13 May 2014 18:16:52 +0900
Q2: 佐藤先生、早速のお返事、誠にありがとうございました。
(1)の文献とフィルタの案、有難うございました。
参考にさせていただきたいと思います。
以下、もう少しお付き合い頂けますでしょうか。
(2)については、私も反射防止膜(ARコート)のような効果は検討しましたが、 以下の理由で除外しました。
 (図5) |
 (図6) |
 (図7) |
1.私どものエピ構造では、サファイア上のGaNの膜厚はMg-GaNとu-GaNを合わせて2.25~3.5μmであり、532nmの1/4波長とは一桁違うこと。GaNの膜厚は下地のu-GaNが2~3μmぐらい、Mg-GaNが250~500nmぐらいです。
Mg-GaNとu-GaNの界面は屈折率差がほぼないでしょうから無視すると、サファイア上に2.25~3.5μmの厚さのGaNが乗っている構造になります。
532nmにおけるGaNの屈折率は2.4ぐらいですので、GaN中の532nm光の波長は222nmぐらいになります。そうすると光路差は膜の往復で波長の20倍以上になります。
2.GaN膜表面の反射率約17%に対して、GaN/Sapphire界面で反射してくる光の強度は、界面の透過率も考慮すると入射光比で1.6%程度となり、オリジナルの反射波の1/10程度の強度でしかなくなること。
仮に膜厚が1/4波長としても、GaN/Sapphire界面で反射してきた光は強度が弱すぎて、GaN表面で反射した光を打消すことは出来ないと考えます。
ちなみにAir/GaN界面では位相がπずれますが、GaN/Sapphire界面では位相がずれないため(Sapphireの屈折率はGaNより小さい)、1/2波長の膜厚が最小反射強度を与える膜厚だと思いますが、いかがでしょう?
いずれにしましてもGaN膜の反射防止効果が最大のときでも、反射波の強度は10%程度しか減少しないというのが私の結論です。
これは正しいでしょうか?
表面パターンは言わば膜厚差であるので、532nmの反射強度の強弱は付く可能性はあると思います。しかし膜厚は波長の20倍もあり、また絶対膜厚は条件により変わるので、極性と532nm強度の関係はランダムでなければならないと思います。しかし実際は、極性と532nm強度の関係は常に不変です。(添付パワーポイント参照下さいませ)
ですので、反射防止膜効果以外に、何か532nm強度に影響するメカニズムがあるのではないかと思案している次第です。
以上踏まえまして、アドバイス頂けましたら幸いです。何卒よろしくお願い申し上げます。
--------------------------------------------------------------------------------------------------------------
Date: Thu, 15 May 2014 00:09:35 +0900
A2: S様、佐藤勝昭です。
本当によくわかりませんね。極性反転が関係するとすれば、下記の様に推察できます。
極性の逆転が起きている領域Bでは、u-GaN/Mg-doped GaNの界面にはチャージの蓄積があり領域Aにおけるu-GaN/Mg-doped GaN界面とは異なります。
Aでは、Sさんの推測のように界面での反射はありませんが、これに対して領域Bでは自由電子プラズマがありこれによる反射があると考えられないでしょうか。
このためB領域ではMg-doped GaN膜が反射防止膜として働くことは十分考えられます。
--------------------------------------------------------------------------------------------------------------
Date: Thu, 15 May 2014 12:40:41 +0900
Q3: 佐藤先生、深夜にも関わらず、メール頂き感激しております。
なるほど、極性反転界面のチャージの蓄積は思いつきませんでした。非常にあり得そうなシナリオですね。Mg-GaNについては、これで納得しようと思います。
残っている疑問は、u-GaN単層のみがサファイアに乗っている単純な構造でも、532nmの強度は通常弱いのです。(強度はほぼゼロ)
何らかの理由でチャージの局在はあるかもしれませんが、反射防止膜として機能する位置にいつも蓄積するとも思えないですし。一方で、サファイアのみで532nmピークが非常に強く出ることも紛れもない事実ですので、悩みます。
反射率スペクトルの測定が出来ればベストだろうと思いますが、なにぶん設備や予算が限られ、ままならないのがもどかしいです。
ともかく、やはり光源に含まれる532nmの強度を、いま一度確認してみようと思います。
何かアイデアを思いつかれましたら、是非ご教授いただきたいですが。
---------------------------------------------------------------------------------------------------------------
Date: Thu, 15 May 2014 14:41:00 +0900
A3: S様,佐藤勝昭です。
u-GaNにおいて、532nm反射が弱いのはふしぎですね。
それを考慮すると,532nm光が1.06μm光のSHGという可能性も捨てきれません。
サファイヤc面やGaNc面結晶バルクからは対称性からSHGはでないはずですが、表面では対称性が破れているので表面でSHGがでないとは言えません。
(Feはbccで対称性からバルクのSHGはありませんが、表面による磁化依存のSHGが観測されます。)また研磨によって結晶性が乱れSHGがでるとも言えるでしょう.
一方,u-GaNエピ膜は結晶性がよく本来SHGはでないし、界面もきれいなのでSHGはでない。
上に摘んだMg-doped GaNが10^20ものMgがはいっているので,結晶性が劣り,u-GaNよりは強いSHGがでる.さらに反転領域では、界面に電荷層が生じ,対称性が破れるためSHGが出る。
この仮説が成立するためには,レーザから1.06μmの光が漏れていることが前提になります。
この点に関しては赤外線カットフィルタの使用によって防げるはずです。 以上,再検討して下さい。
---------------------------------------------------------------------------------------------------------------
Date: Thu, 15 May 2014 15:01:04 +0900
Q3: 佐藤先生、何度もメールでご回答頂き、誠に有難うございます。感激です。
なるほど、最表面の非対称性による非線形光学効果というのもあるのですね。それでしたら納得です。
逆に言えば、消去法でそれしかないということでしょうね。
ちなみに励起光の266nmの倍波長が非線形光学効果で生じるということも考えられますでしょうか?
---------------------------------------------------------------------------------------------------------------
Date: Thu, 15 May 2014 21:12:03 +0900
A3: S様,佐藤勝昭です。
パラメトリック・ダウンコンバージョン(parametric down conversion)ですね。原理的にはありうると思います。 ブラジルの物理研究所のホームページにありますように,ある条件を満たせばエネルギーの高いフォトン(4.66eV)がエネルギーの低い2つのフォトン(エネルギーの和が4.66eV)を発生することが出来ます。
2つのフォトンはエネルギーが同じでなくてもよいので、巾を持ったものになります。以前のあなたのメールで巾が広いのが気になるとご指摘されましたが、パラメトリックダウンコンバージョンであれば理解できます。
これについては、この道の専門家である東北大の片山先生を紹介しますので、そちらにお尋ねください。
------------------------------------------------------------------------------------------------------------
Date: Thu, 15 May 2014 23:13:07 +0900
AA: 佐藤先生、度々のメール有難うございます。2倍波長の発生もありうると言うことですね。
また、片山先生のご紹介有難うございます。先生とのやり取りを整理し直した上で、お伝えしアドバイスを請おうと思います。
一つ思いついたのですが、最表面の構造が問題とのことですので、サファイア基板を水素アニール処理したもののスペクトル測定をしてみようかと思います。
何か変化があれば面白いですね。
この度は本当に親切にご対応頂き、有難うございました。
------------------------------------------------------------------------------------------------------------
[参考](片山准教授からの回答
Date: Sat, 17 May 2014 03:20:02 +0900
|
東北大の片山です、お返事遅れまして申し訳ございません、ご連絡有り難うございます。下記、当方の経験からコメントさせていただきます。 |
|
①波長532nmに検出される光の原因について A)レーザからの2倍波成分 S様・佐藤先生のお考えの通り、YAG4倍波の光源の種類によっては2倍波(532nm)のコヒーレント光が存在します。というのは、4倍波だけ を高強度発生する目的の高調波発生ユニットでは、1倍+3倍の和周波数で4倍波を発生し532nmを介在しないものもありますが、2倍波も利用で きる多くの仕様のレーザユニットですと、2倍+2倍で4倍波を発生するために必然的に532nmの光が混在します。後者の場合で特に、非線形光学 結晶の角度チューニングが狂うと、変換効率が顕著に低下し、二段目の結晶を励起する532nmが抜けてきます。また、安価なKDP結晶を用いる場合 は、266nmを多少吸収して発熱により位相整合条件がずれますので、その場合も特にレーザ立ち上げ初期には532nmの光が抜けやすくなる製品が多 いとメーカの方に伺ったことがあります(BBO結晶を用いると温度変化に鈍感になるのでこれを防げるそうですが、宝石より高いです)。 266nmだけを利用する場合、通常はハーモニックセパレータ(誘電体多層膜ミラー)を用いて532nmを除去するのが得策ですが、一つ5万円ほど と高価でかつ角度がずれると2桁も落とせなくなるので、ウェッジプリズムを用いて266・532nmの二波の光路をより分ける(屈折率分散を利用しま す)のが、最もお手軽かと思います。 B)分光器内での高次回折 Facebookで岩谷先生がご指摘くださったように、グレーティングを用いた分光器内では、望みの波長である1次回折に加えて、比較的高強度な2 次(波長で倍)、3次(3倍)…と高次にあたる角度への回折も起こります。 メーカ製のPLマッピング装置であれば上記の事象を踏まえてあらかじめ適切なオーダーソーティングフィルタが入っているものと思いますが、そ うでない場合は、266nmをカットし測定したい波長域だけを通すフィルタを挿入する必要があります。 参考まで、お使いになった分光器のスペックをお教え頂けますと幸いです。OceanOpticsなどの20万円ほどのコンパクトなファイバマルチチャネ ル分光器でも、購入時に指定すればリニア検出器の特定の箇所に複数のオーダソーティングフィルタを設置し、上記の高次回折を全く気にせずに測 定できる製品があります。それらが分光器内に設置されていない場合でも、シグマ光機などで購入できる安価な色ガラスフィルタで266nmをカットす れば問題無いはずです(余り紫外ぎりぎりのフィルタはありませんが)。ちなみに、下記URLのようなカットオフ比の高い誘電体多層膜ミラーを購入 するのも良いのですが、高価なうえ、透過波長域でも透過スペクトルに周期的なフリンジが重畳することと予期せぬ波長で長波長側のカットオフと なる懸念がありますので、ウェブサイトでダウンロードできる透過スペクトルの数値データを確認してからのご購入をお勧め致します。 |
|
②波長532nmに検出される光の半値幅について こちらもお使いになっている分光器のスペックをお調べ頂くと回答できるのですが、ポータブルファイバ分光器のような短い分光器長のものです と波長分解能はさほど良くないですので、実際は狭線幅であるレーザー光を測定しても、例示頂いたスペクトルのような太いピークとなって観測さ れる場合はよくあります。 ちなみに当方、光パラメトリック下方変換(OPDC)についてもいくらか測定をしておりますが、特段に共振器を組まない限り、単膜における上記 過程は通常のコヒーレンス長からするとその線幅はかなり広くなり、かつシグナル・アイドラの二光子を532nmに縮退させるにはかなり厳密な位相 整合の努力(膜厚均一性や再現性)が必要となるはずですので、拝見したピークは残念ながら(スペクトルを拝見するまで、実はちょっと期待して おりましたが)これが原因ではなさそうです。 ただし、他の項目すべてに該当せず、やはりOPDCであろうということで必要であれば、当方SHGやOPDCの入・出射角依存性を測れるゴニオメータ と266nmのパルスレーザがございます(以前佐藤先生にお世話になり、一式揃えさせて頂いた装置です)ので、反射SHG等の測定を行ってみてもよ いと思います。強くたたけば、反転対称性の破れさえあれば何でも出ます。 |
|
③薄膜干渉効果・AR効果について 「1/4波長で反射が打ち消し」と書かれている部分がありますが、基本的に「(N+1/4)波長で反射が打ち消し(N=0,1,2…)」かと思いますので、ラフネス次第では干渉の効果がでてもおかしくないとは思います。 ただし以下の⑤でコメントしますとおり、干渉というよりは、多分にGaN表面・サファイア基板裏面における散乱の効果が大きいものと考えており ます。 |
|
④格子の極性反転について こちらも皆様のご議論の通りだと察します、Mgのδドープやヘビードープにより、Ga極性がN極性に反転する事象はよく報告されています。一方、 当方の研究室では永らく、Ga極性膜を介さずに直接サファイア上にN極性膜を成膜しておりますが、成長前にサファイアを窒化することがN極性化 のポイントですので、GaNの1000~1100℃での成長前のプロセスシーケンスについても、基板が部分的に窒化されてしまっていないかの検討が必要か と思います(目的がGa極性であることを前提としております。またud-GaNの極性もチェックされると良いかと思います ) なお簡便な極性判定法としては、濃度4~8mol/l、温度40℃程度のKOH水溶液中に数分~30分程度浸漬するだけで、N極性面は容易にエッチング されピラミッド状のモホロジとなります(SEM観察が良いと思いますが、目視でもざらっと白濁するはずです)ので、お試し頂けますでしょうか。 本研究室では、KOHペレットは潮解し、いちいち秤量するのが手間ですので、試薬会社から瓶詰めの濃度の決まった水溶液を購入して使用しており ます。一方、上記エッチング条件では、Ga極性膜はどれだけ成膜条件を外しても(常識の範囲ですが)ほぼエッチングされません。 |
|
⑤波長532nmに検出される光強度の面内での不均一性について まずお使いのPLマッピング装置における、レーザー光の入射角度と、PL光の検出方法を教えて頂けると幸いです。当方が使用していた装置ですと、対物レンズにカセグレン鏡を用いた反射光学系でしたので同軸で入射し、励起光集光角と発光を検出できるアクセプタンス角ほぼ同じでした。平坦で鏡面反射が多い試料表面ほど、励起光が検出される強度が強くなるケースにあたります(もともとラマン用に設計しましたので)。 一方、深紫外レーザで励起となると、励起光は発光検出レンズとは異なる軸で斜入射するケースが多いと思われますので、その場合は、試料表面 が平坦であるほど(領域a?)鏡面反射となるので集光系で検出するレーザ強度は減少し、逆に荒れるほど(領域b?)拡散反射・散乱光として検出系のアクセプタンス角度内に入る励起光の光量が増えます。 |
|
①の原因がAかBかによって解釈は代わるのですが、例えば。 B)もともと266nmの分光器高次回折が原因の場合 ・サファイア基板では、透明なので裏面サンドブラスト領域で散乱光発生・平坦なGa極性領域では、サファイア裏面からの散乱は(GaNの吸収により 到達せず)拡散反射光はゼロ、表面の散乱光もゼロ・荒れたN極性領域では、サファイア裏面はゼロだが、表面の散乱大・上記の高次回折として、266nmの散乱光が532nmに観測される A) もともとレーザに含まれる532nmの光が原因の場合 ・サファイア基板では、表面平坦なので鏡面反射光検出 ・平坦なGa極性領域では、表面平坦で鏡面反射光検出 ・荒れたN極性領域では、表面で散乱され鏡面反射光が顕著に減少 即ち、違いは領域aとbのどちらが荒れているかにかかってきますので、SEMかAFMでのもう少し微視的なモホロジ観察をされると結論に至るように 察します。 |
|
⑥キャリア濃度について 実は当方この点について興味深く思うのですが、MOVPE成長でN極性GaNのp型化に成功したグループは当方の研究室とUCSBだけで、先日弊室の谷 川より電気特性・活性化エネルギ等について評価した結果をJJAP誌に投稿させていただきました(UCSBは電流注入発光できたのでp型のはず、とい う言及に留まっております)。もしN極性化したドメインがp型伝導かつ低抵抗な部位となったとすると私どもの結果と一致しますが、N極性面はMg の取り込み効率がGa極性面より高いと同時に、酸素などドナー不純物も更にたくさん取り込みますので、補償によりなかなかp型化しません。 |
|
⑦図1のモホロジについて 〔※できればスケールバーを表示下さい。〕 ヘビードープにより発生する極性反転ドメインのモホロジについてはあまり見たことがありませんが、水滴状のモホロジを見るとこと、一度Gaド ロップレットが析出した後に窒化されてGaNと成ったようにも見えます。低温緩衝層の成膜時にアンモニアが不足しGaが析出していないかどうかにつ いてもご確認いただけますでしょうか。またGa極性とN極性のGaNの最高成長可能温度も若干差があるとの報告がありますので、サセプタの熱電対 温度や放射温度計温度ではなく実温1100℃を大きく越えて成長していないかと、いずれかのタイミングで基板温度が高いにもかかわらずアンモニア ガスフロー無しとなっていないかについても、ご確認頂けますと幸いです、 また、本研究室の松岡教授はノマルスキ像だけでだいたい成長条件のずれが分かりますので(どちらの極性も)、もしよろしければ基板のオフ角度とその方位、成膜条件等についても併せてお教え頂ければ、相談してみますので宜しくお願い致します。 (メーカー様ということで、多分に現状のモホロジで大変お困りかと思い ますので、本務ということでなければ非線形光学過程については多少後 にまわし、御社でまず必要な平坦膜を作製できる旨い条件を探すお手伝 いするのが先決かと思います。) 取り急ぎです、ご検討いただけますようどうぞ宜しくお願い申し上げます。 |
1323. 金のナノロッドの光学応答
Date: Wed, 18 Jun 2014 14:59:52 +0900Q: 佐藤先生
はじめまして、東工大の修士1年の金沢と申します。
先生のHPを拝見させてもらい、今回、質問を投稿させて頂きます。
下記の内容についてご回答頂けると幸いです。
1.金のナノロッドや回転楕円体など、異方性の構造をもつナノ粒子に光を入射した際、入射光の角度を変えていくと、 これらのナノ粒子の光吸収断面積や散乱断面積といった光学応答は変化するのでしょうか?
先行研究等あまりされていないような内容で、私の見解としては、やはりある角度で吸収が最大になる角度が 存在するのではないかと考えております。
佐藤先生のご見解をお聞かせ願いたいと思います。
2.また、仮にある角度での光吸収のピーク等が存在するのであれば、その角度で光吸収が最大となる原因をお聞かせ願いたいと思います。
お忙しいところ恐縮ですが、よろしくお願いいたします。
----------------------------------------------------------------------------------------
Date: Wed, 18 Jun 2014 19:04:09 +0900
A: 金沢君,佐藤勝昭です。
修士論文の研究ですか?本来,あなたの指導教員か先輩に聞くべきでしょう.
先行研究ありますよ。プラズモニックマテリアル、メタマテリアルなどの世界で多くの研究があります。
入射角依存性の論文の例として,添付ファイルを参考にしてください。
-----------------------------------------------------------------------------------------
1324. 燃焼管内で使えるミラー材料
Date: Mon, 23 Jun 2014 16:43:01 +0900Q1: 佐藤勝昭先生、E*社 O*です。
これまで難題に当たった時はしばしば「物性なんでもQ&A」を参考にさせていただきました。
此の度は、高温燃焼筒中での白金ミラー等の反射率についてご教示をいただきたく、以下におたずねする次第です。
ガソリン燃焼雰囲気内での各種ラジカルの動向を調べるため、波長2.6μm、3.4μmでの吸光度を計測します。
燃焼筒内の発光部と受光部の中間に平面ミラーを置いて光線を往復させ、光路長を稼ぎます。
ミラー周囲の温度は800-1000℃と見込まれます。
このミラーをインコネル601で製作した際は、1時間以上経過すると表面に青灰色の硬い被膜が生じて反射率が次第に低下しました。
また、白金で製作した際は、電気炉内での実験では数時間経過しても問題が無かったのですが、燃焼筒内では30分で表面が曇って反射率が急速に低下しました。
この曇りは白金の触媒作用による生成物のためかと想像しますが、詳細はわかりません。
質問:
① 上記以外に高温での表面反射率がより良く保たれる物質があるでしょうか?
② これらの表面反射率低下を防ぐ方法があるでしょうか?
以上、何とぞよろしくお願い申し上げます。
-----------------------------------------------------------------------------------------
Date: Tue, 24 Jun 2014 13:02:17 +0900
A1: O様,佐藤勝昭です。
① 上記以外に高温での表面反射率がより良く保たれる物質があるでしょうか?
800-1000℃で酸化しないのは金です。その証拠にGold Furnaceという電気炉が
市販されています。http://www.motoyama.co.jp/furnace/gold.htm
② これらの表面反射率低下を防ぐ方法があるでしょうか?
どんな反応が起き,どんな物質ができているのかがわからないと対策の打ちようが
ありません。まずは、それを追求して,それぞれにたいする対策を考えるべきです。
------------------------------------------------------------------------------------------
Date: Tue, 24 Jun 2014 16:43:43 +0900
Q2: 佐藤先生
ご回答ありがとうございました。
①について重ねておたずねいたします。 ご面倒をおかけしますが、よろしく お願い申し上げます。
① 金については融点1063℃とは言え周囲温度がかなり近くなることに不安が
あります。 (SUS板に金薄板を融着したテストでは加熱後表面が粗くなり
使えませんでした。 結晶粒粗大化?)
Au-Pd-Pt合金(例えば添付の陶板焼付用合金 KIK:石福金属製)を採用し
た場合、融点(固相線)が1200℃くらいに上がると期待されますが、800-
1000℃での表面反射率、耐酸化性、触媒の性質などがどのようになると予
測されるでしょうか?
② の生成物質が何かを調べることを検討します。
酸化膜や不働態層であっても、それが対象波長を良く反射してくれればOK
なのですが、これまでのところそうなりません。
以上
-------------------------------------------------------------------------------------------
Date: Tue, 24 Jun 2014 18:19:46 +0900
A2: O様,佐藤勝昭です。
① 金ではダメですか。Au-Pdは歯医者で使う合金ですね。比率が書いて
ないのですが、Pdが多いと触媒作用があるかも知れません。
触媒作用で物質が合成されて付着することがなければ、高温になっても
反射率に大きな変化はないと思います。ガソリンに硫黄分があると
表面がやられる可能性があります。
② はじめから薄い酸化物保護膜で金属を覆っておけば、赤外の反射特性は
保たれて腐食には強くなるのではないでしょうか.
------------------------------------------------------------------------------------------
Date: Tue, 24 Jun 2014 19:30:42 +0900
AA: 佐藤先生
再度のご回答ありがとうございました。
金及び金合金での検討を進めてみます。 酸化物層を保護膜として機能させ、且つ反射(透過)性が保たれるとたいへん
ありがたいです。 セラミックコーティングなどを含めて可能性を調べてみ
たいと存じます。
-------------------------------------------------------------------------------------------
1325. 金属光沢の説明
Date: Sun, 6 Jul 2014 00:26:31 +0900Q1: 佐藤勝昭 様
はじめまして。
私は愛知県で高等学校の教員をしておりますIと申します。
金属光沢を分かりやすく生徒に伝えようと思い、学術的な背景を調べる中で先生のHPにたどり着きました。
HP内の物性工学概論(2006)の第3回の資料に、束縛された電子についてローレンツの式を用いての説明がありますが、 この説明の解釈について、またそれによる金属光沢の色味についての説明は、以下の解釈で正しいのでしょうか。
①束縛された電子は内殻電子のことである。
②ゆえにローレンツの式が適用される電子系とドルーデの式が適用される電子系は別々の電子系として議論してよい。
③バンド間遷移についても同様に解釈して、固体金属の内殻電子についてはバンドギャップが絶縁体のように大きいと考える。
④また、そのバンドギャップのエネルギー差が誘電率の急落に対応している。
⑤よって内殻電子のバンドギャップが大きい一般的な金属では銀のような金属光沢を示すが、
金や銅などはそのバンドギャップが比較的小さく、可視光域の光を吸収するために呈色する。
私の調べた範囲では、以上の内容が一番しっくりくるのですが、そのような解釈による説明は見当たらなかったで、 質問させていただいた次第です。
おそらく束縛電子についての解釈と、バンド間遷移についての私の理解が乏しいことによる質問になりますので、この辺りを詳しくご教授願いたいと思います。
また、花村榮一「固体物理学」のバンド間遷移による金属プラズモンの説明を読んで理解を深めようと思ったのですが、
⑥先生の仰るローレンツの式による束縛電子の影響は、バンド間遷移の電子分極への寄与と考えて差し支えないのでしょうか。
質問は以上です。お忙しい中とは思いますが、よろしくお願いします。
------------------------------------------------------------------------------------------
Date: Sun, 6 Jul 2014 00:55:03 +0900
A1: I様、佐藤勝昭です。
メールありがとうございます。ローレンツ計とドルーデ系が別々の電子という点は、I様の解釈でOKですが、 束縛電子についてやや誤解がありますので、訂正しておきます。
物性工学概論において束縛電子モデルを使ったのは、バンド間遷移による価電子の励起の寄与をローレンツモデルで扱うという意味で、 束縛電子と表現したわけで、内殻電子の励起では決してありません。内殻電子の励起はX線の領域に来ます。
金属においてもバンド間遷移が考えられ、実際Auのプラズモン周波数はAuの5dバンドからフェルミ面への遷移の周波数に相当します。
スペクトルは量子力学を用いた計算でも、近似的にローレンツ型の重ね合わせになりますので、古典的な束縛電子モデルを使っても、 スペクトルを近似するには差し支えないのです。
これについては、トライボロジスト誌に書いた解説「金属の色と金属光沢」をお読みください。
-------------------------------------------------------------------------------------------
Date: Sun, 6 Jul 2014 02:50:10 +0900
Q2: 佐藤勝昭 様
夜の深い時間にもかかわらず、素早い返信感謝いたします。
先生の説明によって私の理解が少しクリアになりました。
バンド間遷移による価電子の励起の寄与をローレンツモデルで扱うという意味で、束縛電子と
表現したわけで、内殻電子の励起では決してありません。内殻電子の励起はX線の領域に来ます。
金属においてもバンド間遷移が考えられ、実際Auのプラズモン周波数はAuの5dバンドからフェルミ面への遷移の周波数に相当します。
つまり、5d軌道の電子も金属中ではバンドを形成しており、非局在化してい ないために固有のバンドギャップを 持つが、その軌道内のバンドギャップのエネルギーは大きく、X線のエネルギーに相当している。
5dバンドの価電子帯の電子は、6sバンドのフェルミ面に励起することができて、これをバンド間遷移と表記している。ということでしょうか。
また、お示しいただいた試料中の鉄の項目についてですが、鉄のバンド間遷移のエネルギーは金や銅に比べて 低く、可視光域の全領域にわたって価電子による反射を低下させると考えるのは不適当なのでしょうか。
ずうずうしくも新たに質問させていただきますことお許しください。
--------------------------------------------------------------------------------------------
Date: Sun, 6 Jul 2014 08:54:31 +0900
 A2: I様、佐藤勝昭です。
A2: I様、佐藤勝昭です。私の説明が悪く誤解を招きました。Auの5d軌道は閉殻(M殻)を作っておりますが狭い(状態密度の高い)バンドを作っており、「M殻→フェルミ」の遷移は バンド間遷移と見なし、内殻遷移とは考えていません。
私が内殻遷移と言ったのは、「Auの5d軌道内のバンドギャップ間遷移」ではなく添付図に示したように、X線でK殻(1s)電子が励起されM殻から電子がK殻ホールに 遷移するようなものを指しております。
Feの3d軌道は幅の広いバンドを作っていて、Auに見られるような明確なエッジが見られません。さらにフェルミ面に有効質量の大きなd電子が混成しているので 自由電子プラズモンのダンピングが大きく、ε'が負の大きな値になることを抑えているので反射率が高くないのではないかと思います。
--------------------------------------------------------------------------------------------
Date: Sun, 6 Jul 2014 11:56:09 +0900
AA: 佐藤勝昭 様
返信ありがとうございます。
Auの5d軌道は閉殻(M殻)を作っておりますが、狭い(状態密度の高い)バンドを作っており、 「M殻→フェルミ」の遷移はバンド間遷移と見なし、内殻遷移とは考えていません。
私の解釈の中の「その軌道内のバンドギャップのエネルギーは大きく、X線のエネルギーに相当している。」という部分に誤解があるということですね。
内殻遷移についてはこの場合特に考える必要はなく、5d軌道に収容された内殻電子のフェルミ面への遷移を議論していると解釈しておけばよいのでしょうか。
Feの3d軌道は幅の広いバンドを作っていて、Auに見られるような明 確なエッジが見られません。
鉄の場合内殻電子が閉殻構造をとっていないことを失念しておりました。貴金属系ほど単純な議論はできなさそうですね。
--------------------------------------------------------------------------------------------
1326. 運動する点電荷の式を金属中に適用するには
Date: Mon, 30 Jun 2014 17:03:47 +0900Q1: 佐藤勝昭 先生: K*大学教員W*と申します.
--------------------------------------------------------------
●(Lienard-Wiechertポテンシャル を経て求めた) 運動する点電荷がつくる電場を表わす
(添付のpdfファイルの4ページめの)式(13)は,
(暗に/当然に)「真空」中を運動する点電荷についてのものであると理解しますが,
この式(13) (or 添付のpdfファイルの考え方) を「金属」中を運動する自由電子がつくる
(金属内における)電場に応用することは可能でしょうか?
※(表層的に推測すると)
式(13)中の真空中での電磁波の伝搬の速さcを金属の複素屈折率(光学定数)n^ (=n+ik)
あるいは (複素屈折率の実部の)屈折率nを用いて
c → c/(n^)
c → c/n
の置き換えを行うのでは? と思ったのですがいかがでしょうか?
--------------------------------------------------------------
見当外れの質問である場合は ご容赦下さい.
よろしくお願い申し上げます.
------------------------------------------------------------------------------------------
Date: Sat, 5 Jul 2014 18:46:49 +0900
A1: 様、佐藤勝昭です。
お返事が遅くなって申し訳ありません。
ご質問の趣旨は、真空中で運動する電子に適用される電場の式が、金属中の環境を複素誘電率に
押し込めれば、そのまま適用できるかということでしょうか。古典的な電磁気学では金属中では
電界がないとしているので、ミクロな立場で固体物理学の考え方で扱わなければなりません。
金属中では、電子が電子の海の中を運動するので、多体問題になります。電子間相互作用をどう
扱うか。多体効果を取り入れた金属のバンド構造や電子散乱まで考えるとはたして複素誘電率に
おしつけて真空中で成立する式が適用できるのか分かりません。
いま、理論屋さんに問い合わせているところです。
------------------------------------------------------------------------------------------
Date: Wed, 16 Jul 2014 16:43:22 +0900
A1': W様,佐藤勝昭です。
東工大理学部の村上修一教授に問いあわせていましたが、本日,下記のような回答がありました。
複素屈折率の周波数依存性の考慮が必要とのことです.
(前略)ご指摘のとおり、金属のバンド構造や電子散乱は特に複素屈折率の周波数依存性に大きく
影響を及ぼしますので、Lienard-Wiechertポテンシャルを適用する際に複素屈折率の周波数依存性を
入れる必要があると考えられます。
特にLienard-Wiechertポテンシャルを考えるということは非常に短時間の物理なので、電荷の運動に
対し周囲(他の電子、格子)がどのくらい速く反応するか、という問題が強く効くはずです。
格子はそんなに速く反応しないですが、他の電子は素早く反応するはずなので、複素屈折率は今考えて
いる周波数に大きく依存し、その周波数依存性を無視することはできないと思います。
-------------------------------------------------------------------------------------------
Date: Thu, 17 Jul 2014 13:44:11 +0900
Q2: 佐藤勝昭 先生 村上修一 先生、です.
大変おいそがしいところ回答下さりありがとうございました.
(もう少しだけ質問させていただいてもよろしいでしょうか?)
『複素屈折率の振動数依存性を考慮する』ということは,
(式(13) あるいは) 式(13)の直前の
E(r,t)=-∇φ(r,t)-{∂A(r,t)/∂t}
[※c → c/(n^) の置き換えを行った]
の両辺をFourier変換して 角振動数ω領域において
電場E(=E(r,ω))を求めるということでしょうか?
よろしくお願い申し上げます.
---------------------------------------------------------------------------------------------
Date: Thu, 17 Jul 2014 15:11:09 +0900
A2: W様,佐藤勝昭です。
『複素屈折率の振動数依存性を考慮する』ということは,c*=c/n(ω)にしなければならないということです。
(13)式をフーリエ変換するだけでは説明できないのではないでしょうか?
----------------------------------------------------------------------------------------------
Date: Fri, 18 Jul 2014 11:53:18 +0900
Q3: 佐藤勝昭 先生:
Wです.ご回答ありがとうございました.
昨日(20140717)の私からの質問は,
『複素屈折率の振動数依存性を考慮する』ということは,
(式(13) あるいは) 式(13)の直前の
E(r,t)=-∇φ(r,t)-{∂A(r,t)/∂t}
[※c → c/(n^) の置き換えを行った,
たとえば 金属として 銅を想定して
銅の複素屈折率スペクトルn^(=n^(ω))は
減衰項ありのDrude分散式に従うとする]
・・・ 式(13+)と呼ぶ
の両辺をFourier変換して 角振動数ω領域において
電場E(=E(r,ω))を求めるということでしょうか?
とすべきでした.
以下は, 「振動数依存性を考慮する」こと と「Fourier変換する」こと
の関係について 昨日先生にお聞きしたかったことを書きますが,
(意図不明)・(的外れ)・(基本理解不足)などであれば ご容赦下さい
.
(複素屈折率n^の分散式が既知であるとすれば 任意の角振動数ωについて n^の値が既知であり,)
ある(1個の)ωについて(も) n^の値は既知であり,そのn^の値を式(13+)の右辺に代入すれば
(式(13+)の両辺を(わざわざ)Fourier変換しなくてもそのまま)時刻t領域において あるωについて
(さらに 別の(いろいろの)ωについても同様に) 式(13+)の右辺が 見かけ上 計算できてしまうよう
に思えるのですが,そのような簡単なことをもって 振動数依存性を考慮したと言えるでしょうか?
------------------------------------------------------------------------------------------------------
Date: Mon, 21 Jul 2014 14:51:52 +0900
A3: W様、佐藤勝昭です。 あなたのご質問が、あくまで古典的なLienard-Wiechertポテンシャルの近似の範囲で見かけの複素屈折率を使え
ないかということでしたから、ある周波数範囲のもとで、n(ω)を使ってもよいと答えただけです。
周波数に依存するということは時間依存をきちんと扱う必要があって、ご存知のように久保公式を使う必要があります。
このときに、現象として、電子との相互作用をどこまで取り入れるかということだと思います。村上先生のご指摘のように、
格子との相互作用と電子との相互作用では時間スケールが異なりますが、これを全て取り入れて久保公式で計算すれば、
誘電率、従って、複素屈折率の周波数依存性も全部表すことができるでしょう。 この計算は大変面倒ですが、Wさんが挑戦してみてはいかがでしょうか?
-------------------------------------------------------------------------------------------------------
Date: Wed, 23 Jul 2014 08:00:24 +0900
AA: 佐藤勝昭 先生:
K大・Wです.
お礼が大変遅くなり申し訳けございませんでした.
ご回答ありがとうございました.
先生からいただいた(考え方・キーワード)を (私の中で消化してから)
いま私が計算したい対象の系にどのように取り込むかを考えたいと思います.
------------------------------------------------------------------------------------------------------
1327. 磁気光学効果における磁場の効果
Date: Sat, 19 Jul 2014 21:11:17 +0900 Q1: 佐藤先生、はじめまして私は京都大学3年の古賀と申します。
磁気光学効果における磁場の寄与について質問させて頂きます。
佐藤先生の著書「光と磁気」を読んでいて気になったことがあります。磁気光学効果とは、「ゼーマン効果(または交換分裂
)によってスピン状態が分裂し、さらにスピン軌道相互作用によって軌道状態が分裂することによって、左右円偏光に対する
遷移エネルギーに差が出る」現象であると解釈しています。
しかし、スピン状態の分裂が交換分裂によって起こるなら、外部磁場の効果が全く無いように思います。磁気光学効果は、
外部磁場が無くても起こるということでしょうか?
また、外部磁場によるゼーマン効果で軌道状態が分裂し、それによって磁気光学効果が起きるということはないのでしょうか?
(ゼーマン効果は磁気量子数と磁場の積に比例してエネルギーが変化する現象でもあるはずです。)
以上の2点についてお答えいただければ幸いです。よろしくお願いします。
-------------------------------------------------------------------------------------------------------
Date: Sun, 20 Jul 2014 01:02:52 +0900
A1古賀君、佐藤勝昭です。拙著「光と磁気」をお読みいただき感謝します。
(1) 強磁性体における交換分裂では↑スピンと↓スピンが分裂し、 低温では↑スピンの準位にのみ分布するので磁界が必要ないように 思えますが、強磁性体の初磁化状態では、全体が磁区に分かれていて、 磁化が消えています。すなわち↑と↓が同数になっています。
これでは、磁気光学効果は出ません。
磁界を加えて磁気飽和させれば(単磁区になるので)磁気光学効果が生じます。アイソレータの磁石は、磁区を揃えるためにあるのです。
(2)遷移金属の軌道磁気モーメントは殆ど消失しているので、
これによるゼーマン効果は無視できます。
---------------------------------------------------------------------------------------------------------
Date: Sun, 20 Jul 2014 02:00:20 +0900
Q2: 佐藤先生、夜分遅くに申し訳ありません。
古賀です。ご回答頂き、誠にありがとうございます。
(1)については納得しましたが、(2)についてまだ疑問に思うところがあります。大変恐縮ですが、もう一度ご教授頂ければ幸いです。
d電子の基底状態における軌道角運動量Lは0としてよいので、この状態において正常ゼーマン効果が起きないことは理解できます。
しかし、L=0の基底状態に左右円偏光が当たってLz=±1となったp電子的な励起状態では、やはりゼーマン分裂が起きるのではないでしょうか。
つまり、スピン軌道相互作用によってエネルギーが分裂するだけでなく、励起状態の軌道磁気モーメントと外部磁場による分裂も起こるのではないかと考えています。
この点についてお答え頂けると幸いです。
---------------------------------------------------------------------------------------------------------
Date: Sun, 20 Jul 2014 10:48:33 +0900
A2: 古賀君、佐藤勝昭です。
勉強熱心ですね。自主的に勉強して、どんどん進んで下さい。
さて、ご質問の励起状態の軌道角運動量ですが、それは、十分に取り込まれています。
なぜなら、励起状態においては、Sはもはやよい量子数ではなく、Jがよい量子数になるからです。
p電子軌道の場合、Jz=+3/2,+1/2,-1/2,-3/2となります。
強磁性の場合、基底状態がJz=+1/2であれば、
右回り円偏光によって、+1/2→+3/2の遷移が許容
左回り円偏光によって、+1/2→-1/2の遷移が許容
となります
励起状態のJz=+3/2と+1/2のエネルギー間隔は殆どスピン軌道相互作用(3d系で500cm^-1のオーダー)
できまり、外部磁界のゼーマンエネルギーは、B=1Tにおいてもせいぜい数cm^-1のオーダーなので、
無視することができるのです。
なお、希土類の基底状態では軌道が生きているので、軌道のことを十分考慮する必要があります。
----------------------------------------------------------------------------------------------------------
Date: Sun, 20 Jul 2014 19:50:37 +0900
Q3: 佐藤先生
古賀です。詳しい説明ありがとうございます。
計算してみると先生のおっしゃった通りになりました!
何度も申し訳ありませんが、もう一つ伺ってもよろしいでしょうか。
私はp軌道がスピン状態で分裂し、アップスピン状態にL=(0,0,±1)のスピン軌道相互作用、ダウンスピン状態にL=(0,0,±1)が
内積としてかかり(H=λS・L)、それぞれが2つずつに分裂すると解釈しています。
この4つの状態がそれぞれJz=+3/2,+1/2,-1/2,-3/2に対応するからJがよい量子数になる、と考えて良いのでしょうか?
「よい量子数」に対する理解が不完全なため混乱しております。
----------------------------------------------------------------------------------------------------------
Date: Sun, 20 Jul 2014 20:39:17 +0900
A3: 古賀君、佐藤勝昭です。
量子力学で摂動論を学ばれたと思います。本当は、全ての相互作用を一度に 扱わなければならないのですが、スピン分裂>スピン軌道 として、スピン軌道 を摂動として扱うというのが、あなたの解釈です。
結果的には、状態をL単独でもS単独でも表せず(=よい量子数ではなく) J=L+Sを使って状態を表せる(=よい量子数になる)のです。
-----------------------------------------------------------------------------------------------------------
Date: Sun, 20 Jul 2014 21:08:01 +0900
Q4: 佐藤先生
古賀です。ご回答ありがとうございます。
つまり、ある量子数Aに対して
H=H0+H'(A)
として表せるようなAがよい量子数という解釈でいいでしょうか?
------------------------------------------------------------------------------------------------------------
Date: Sun, 20 Jul 2014 22:22:54 +0900
A4: 古賀君、佐藤勝昭です。 「量子力学において、ある物理量の固有状態が同時に定常状態にもなっている時 (つまりハミルトニアンと可換な時)、その物理量の固有値を良い量子数という。」
となっております。(wikipedia)
H=H0+H'(A)かつ[H,A]=HA-AH=0
である必要があります。
------------------------------------------------------------------------------------------------------------
Date: Sun, 20 Jul 2014 22:34:48 +0900
AA: 佐藤先生 古賀です。何度も質問にお答え頂き、本当にありがとうございました。非常に勉強になりました。これからも先生の「光と磁気」やHPで勉強に励みます。
------------------------------------------------------------------------------------------------------------
1328. 高比透磁率材料の厚さと磁気飽和、飽和磁束密度の関係
Date: Mon, 14 Jul 2014 06:58:48 +0000 Q1: 佐藤勝昭先生、K*社のE*と申します。
Q1: 佐藤勝昭先生、K*社のE*と申します。書籍を若干読んだ程度の知識で申し訳ありませんが、材料の飽和磁束密度について調べていた所、こちらの存在を知り、 勝手なお願いながら教えていただければとメールした次第です。
まず概要を説明させていただくと。
現在、残留磁束密度1.3Tほどの円柱形磁石を連結したリニアレールの上に、20mmほど離して150mm四方の板状パーマロイPB材1mmを 重ねて磁界を遮る事を試みています。
さらに外側は2cmほど開けてパーマロイを挟み込む様に数mm厚の処理鋼板で挟む配置となっています。
通常、パーマロイは比透磁率の高さを利用して保護対象を囲みこむ使い方が一般的ではありますが、 囲み込む使い方でできず「壁」を作るような方法をとっています。
結果、テスラメータでPB材1枚で両面垂直方向の磁束密度は、磁石側で40mT、反対側で数~1mTほど となり、数枚重ねても反対側の磁界を消すことはできませんでした。
この現象をメーカー問い合わせした所、40mTの磁束密度に1mmのPB材では飽和しているとの見解が出てきましたが、
ここで
・PB材の磁束飽和密度1.5Tでかかってる磁束密度より大きい
・磁束密度の単位はT(テスラ)= Wb/m2で単位上厚さは無関係
の2点から材料の厚さでは磁気飽和しないのでは考えたものの、メーカーからはそれ以上の情報は得られず、 現象に対する根拠が明確にできず困っております。
つきましては
・材料の厚さと磁気飽和、飽和磁束密度の関係
・厚さと反対側の磁界が磁気飽和と無関係の場合どのような現象が考えられるか
を教えて頂けないでしょうか
申し訳ありませんが宜しくお願いします。
----------------------------------------------------------------------------------------------------------------
Date: Wed, 16 Jul 2014 18:28:37 +0900
 A1: E様,佐藤勝昭です。
磁気シールド板内では、高い透磁率のために磁力線は、板の中を面に平行に流れるのですが、
PB材のBH曲線(添付図)で見る限り、40mT=400Gauss=32000A/mも印加すると飽和領域に入っていて、
透磁率はかなり小さくなっているのではないでしょうか.
A1: E様,佐藤勝昭です。
磁気シールド板内では、高い透磁率のために磁力線は、板の中を面に平行に流れるのですが、
PB材のBH曲線(添付図)で見る限り、40mT=400Gauss=32000A/mも印加すると飽和領域に入っていて、
透磁率はかなり小さくなっているのではないでしょうか.また、PB板端面からの磁力線は、遮蔽鋼板との隙間を通って回り込みます。
なお、添付図だけでは,状況が分かりません。
円柱状の磁石の長さとPB板の関係が分かりません。図から見る限り磁石の円形断面が磁極となって紙面に 垂直に強い磁界が出ているはずです。できれば立体的な図を描いて頂けないでしょうか
----------------------------------------------------------------------------------------------------------------
Date: Fri, 18 Jul 2014 08:11:20 +0000
 Q2: 佐藤勝昭先生、Eです。お世話になっております。
Q2: 佐藤勝昭先生、Eです。お世話になっております。連絡ありがとうございました。
書いて頂いた内容を読んで、自分が飽和磁束密度=飽和しない磁界の上限と勘違いしてしまっていたことに気づくことができました。
初心者ということを差し引いてもお恥ずかしい限りです。
ただ、悲観しているばかりいても、パーマロイ反対側まで達した磁界が消えるわけでもなく、申し訳ありませんがもう少し教えて頂ければ幸いに思います。
立体的な図を書くのが得意ではないため、今回参考として立体的が全体の概略図と、リニアレールの構成、寸法を入れた平面図を添付させて頂きました。
それぞれの配置は一番上の図の全体構成にあるとおり、処理鋼板に挟まれた場所にリニアレールが固定され、その上をパーマロイが貼り付けられたステージが 移動する様になっています。
保護対象は図中に記載しました様にφ52mmのPMTで、ここに達する磁界を数十uTまで低減する検討を行っている次第です。
前回質問させて頂いた内容は、パーマロイと厚さ・飽和の関係が理解できず教えて頂きたいと言う内容でしたが、この件に関して、下記の内容について教えて頂けな いでしょうか。
素人質問で申し訳ありませんが宜しくお願いします。
<質問事項> ・磁束密度は、外部から磁界を与えることで発生する磁界。その磁界が増えなくなる点が飽和磁束密度となっています。
これは単純にパーマロイが弱い磁界を与えることでB-H曲線にある磁束密度をもつ磁石になると言うことでしょうか。
それとも、磁束を通せると言う意味でしょうか。
・パーマロイPB材と一番近い処理鋼板の隙間から磁界が吹き上がっているとの指摘を 頂き、磁界が隙間から回り込みんでいる事は理解しました。
構造上の制約からこの磁界を現状のようにリニアレールと平行に配置された防磁手段だけで遮る必要があるのですが、可能でしょうか。
また、なにかよい手段は有りますでしょうか。
・パーマロイ1mmを数枚重ねても、保護対象への磁界が無くならず、保護対象の防磁策としてシールド施設の様に空気層を入れて対策を取る事位しか思い浮かびません。
この時、空気層の厚さと磁界の減衰にはどのような関係があるのでしょうか。
単純に比透磁率と距離を抵抗成分と見立てて計算して良いものでしょうか。
-----------------------------------------------------------------------------------------------------------------
Date: Mon, 21 Jul 2014 13:41:14 +0900
.jpg) A2: E様、佐藤勝昭です。
A2: E様、佐藤勝昭です。質問(1)単純にパーマロイが弱い磁界を与えることでB-H曲線にある磁束密度をもつ 磁石になると言うことでしょうか。それとも、磁束を通せると言う意味でしょうか
答え:パーマロイは軟磁性なので、わずかな磁界で大きな飽和磁束密度をもった磁石に なります。従って、磁路を閉じない限り、端面から大きな磁束がでます。
質問(2)リニアレールと平行に配置された防磁手段だけで遮ることは可能でしょうか。
添付図proposal(1).jpgのように隙間が少なくなるように、シールドが壁から出ていて重なるようにしてはいかがでしょうか
.jpg) 質問(3)空気層の利用
質問(3)空気層の利用あまり意味がありません。磁気シールドの対象がフォトマルのみであれば、フォトマル部分をシールドすることを考えた方がよいのではないでしょうか。
私は、磁気光学効果の測定のために、図proposal(2).jpgのような形でフォトマルを磁気シールドしていました。
------------------------------------------------------------------------------------------------------------------
1329. 鉄と酸化鉄の比透磁率
Date: Thu, 24 Jul 2014 18:43:42 +0900Q1: 佐藤先生
はじめまして、X社にて開発を行っておりますO*と申します。 お忙しいところ、申し訳ございませんが、教えて頂きたいことがございまして、メールさせて頂きました。
開発には関係ないのですが、鉄と酸化鉄の比透磁率を調べております。
いろいろ探したのですが、其々の質量磁化率しか見つけられませんでした。
そこで、質量磁化率から透磁率を求めることとし、以下の式にならって計算を致しました。
μ=1+κ-①
μ:比透磁率(単位:無次元)
κ:体積透磁率(単位:無次元)
κ=Χxσ-②
Χ:質量透磁率(m3/kg)
σ:比重(kg/m3)
①に②を代入して
μ=1+Χσ
鉄の体積磁化率は0.022(SI単位に換算すると0.27)であったので代入すると
比透磁率μ=1+0.27=1.27
となりました。
しかし、一般的に鉄の透磁率は5000程度との記述を見つけました。
計算のどの部分が間違っているのでしょうか。
同様に他の化合物に関しても計算しているのですが(下表)
、 鉄の数値がかけ離れているので、その他の化合物に関しても間違っていると考えております。
| 化合物 | 比重 | T | Χg 質量磁化率 | κ 体積磁化率 | K | |||
|---|---|---|---|---|---|---|---|---|
| g/cm3 | kg/m3 | K | 10-6cm3/g | m3/kg | (無次元) | SI単位に換算 | (無次元) | |
| α-Fe | 7.874 | 7874 | 293 | 217.6 | 0.000003 | 0.02153 | 0.27 | 1.27 |
| FeCl2 | 3.16 | 3160 | 293 | 116.4 | 0.000001 | 0.00462 | 0.06 | 1.06 |
| FeO | 5.7 | 5700 | 293 | 100.2 | 0.000001 | 0.00718 | 0.09 | 1.09 |
| Fe3O4 | 5.17 | 5170 | 293 | 91.2 | 0.000001 | 0.00593 | 0.07 | 1.07 |
ご返信頂けますと幸いです。
宜しくお願い申し上げます。
-------------------------------------------------------------------------------------------------------------
Date: Fri, 25 Jul 2014 19:21:53 +0900
 A: O様、佐藤勝昭です。
A: O様、佐藤勝昭です。磁化率χはχ=M/Hで定義されますが、磁化Mが磁界Hに比例することが前提です。
従って、常磁性体、または、強磁性体のT>Tc、フェリ磁性体のT>TNの常磁性領域 でのみ定義できます。あなたの示されたαFeの0.022という値はT>Tcの値でしょう。
αFe(強磁性体)はT<Tc、Fe3O4(フェリ磁性体)はT<TNで自発磁化を持ちます。
すなわち、磁界Hを加えなくても有限の磁化Mを持ちます。
磁化率χをχ=M/Hとすると、H=0でも0でないMがあるのでχは発散してしまいます。
従って、普通の磁化率の表には載っていないはずです。例えば、
Magnetic Susceptibility
それでは、強磁性体の磁化率とはどういう定義なのでしょう?
添付図は、強磁性体・フェリ磁性体のB-Hヒステリシスです。初磁化状態では、 強磁性体が磁区に分かれるため、H=0でB=0になっており、磁界を加えると磁壁が 動いてBが生じます。このときのB/Hが初透磁率μ_iです。
この値は、試料毎に異なりますが、Fe(99.8%)の場合、5000、Permalloy の場合8000と書かれています。
--------------------------------------------------------------------------------------------------------------
Q2: 佐藤勝昭先生
ご回答ありがとうございます。
匿名でお願いしておりますOです。ご返信遅くなり申し訳ございません。
書籍に記載ある強磁性体の磁化率は、キュリー温度以上における磁化率なのですね。
つまり、質問させて頂いた式①は、キュリー温度以下では成立しないことに納得出来ました。
お忙しい中、ご丁寧なご説明ありがとうございました。
先生のご説明の中でわからないことが1点ございましたので教えて頂けますと幸いです。
私の理解として「Fe3O4は強磁性体である」というのが前提となります。
前提に誤りがございましたら、ご指摘いただけますと幸いです。
〇教えていた頂きたいこと
先生のコメント
「Fe3O4(フェリ磁性体)はT<TNで自発磁化を持ちます」
ここで言うTNは、反強磁性転移温度でよろしいでしょうか。
その場合、
「Fe3O4とは、TN以下の温度では、強磁性体であり、TN温度以上になると反強磁性体になる物質」
との認識でよろしいでしょうか。
申し訳ございませんが、よろしくお願い申し上げます。
--------------------------------------------------------------------------------------
Date: Fri, 1 Aug 2014 16:25:20 +0900
A2: O様。佐藤勝昭です。Fe3O4(magnetite)はフェリ磁性体です。
フェリ磁性体は、反強磁性体の一種で、↑と↓の副格子磁化にアンバランスがあって正味の 自発磁化が出ている状態です。フェリ磁性体が磁気秩序を失う温度は、反強磁性体と同じく ネール温度TNといいます。従ってT<TNでは自発磁化があり、T>TNでは常磁性になります
--------------------------------------------------------------------------------------
Date: Mon, 4 Aug 2014 09:51:04 +0900
AA: 佐藤勝昭先生
ご回答ありがとうございます。
フェリ磁性体が反強磁性体の一種であることを理解しておりませんでした。
最後までご丁寧に解説いただきましてありがとうございました。
--------------------------------------------------------------------------------------
1330. 結晶中の原子の座標・配位数
Date: Fri, 8 Aug 2014 08:07:27 +0000Q: 大変お世話になっております、Z社のYです。
初めてこちらに質問させて頂きます。
お忙しい中、無償でこのようなご指導を続けられていること心からご尊敬申し上げます。
以下の二点に関しまして、ご質問させて頂きます。
(1) 並進対称性のみの結晶構造の原子座標の決め方について
単結晶X線回折や粉末X線回折や中性子線回折のリートベルト解析などで導き出される結晶の原子座標に関してです。
その結晶が回転軸や鏡映面等を持っている場合は対称性が最適になるように原子座標が決定されるのだろうと想像しておりますが、 対称性の低い結晶の場合は、原子座標の原点はどのように決定されるのでしょうか。
例えば空間群Pna21の場合、z軸方向は並進対称性しかないように思われますので、z軸方向の原点、(001)面を どこに置いても並進対称性は得られてしまうように思われます。この場合、同様な結晶構造の試料群を複数測定した場合に、 試料毎に少しずつ異なるz座標が得られたりするわけですが、z座標が異なるということは何を意味するのか、分からなくなってまいりました。
(2) 結晶構造における配位数の決め方について
ぺロブスカイト構造のAイオンBイオンのように配位数が判りやすいものの場合はよいのですが結晶構造が複雑で中心金属イオンと 周囲の陰イオンとの結合距離がまちまちな場合、どこまでを配位していると考えるものなのでしょうか。
指標が有りましたらご教示いただきたく思います。
いずれも基礎的なことでお恥ずかしい限りです。どうかよろしくお願い申し上げます。
-------------------------------------------------------------------------------------
Date: Sun, 10 Aug 2014 21:49:14 +0900
A: Y様、佐藤勝昭です。
お返事が遅くなり申し訳ありません。私は結晶構造解析は専門外なので自信 はありませんが、私の理解している範囲でお応えします。
(1)本来並進対称性をもつ場合の格子点は単位胞のどこにとってもよいのです.
すべての格子点には原子団による単位構造が配置されています.単位構造内の 原子は1つあるいは複数個から成っていて、単位構造内のj番目の原子の位置 を単位構造の位置する格子点を原点として,
rj= xja1 + yja2 + zja3,
と表します。 原点は,0 ≦ xj, yj, zj ≦ 1 のようにとることができます。
ご質問のでは、z方向に並進対称性しかかない場合、同様な結晶構造の試料群 を複数測定した場合に試料毎に少しずつ異なるz座標が得られたりするとのこと ですが、単位構造内の原子のz座標の相対位置のみに意味があるのだと思います。
(2)結晶構造における配位数の決め方について
配位数は、結晶学では、注目する原子の最近接の原子数と定義されます。
一方、化学では、分子やイオンの結合性を重視して、注目する原子と結合して いる他の原子の数となっています。有機物における炭素の結合についてはσ 結合のみがカウントされ、π結合はカウントされません。従って、複雑な結晶 の場合、どこまでを結合していると見るかは微妙です。通常は、原子間距離の 閾値を与えて、それより短い原子の数を数えるようです。例えば、
J. Chem. Software, Vol. 7, No. 2, p. 47?56 (2001)
準結晶やアモルファス金属などの場合、EXAFSなどで求めた動径分布関数を 最初の極小値の距離まで積分して、配位数を算出しています。
というわけで、配位数の決定にはやや任意性が入ると思います。
--------------------------------------------------------------------------------------
Date: Mon, 11 Aug 2014 00:42:32 +0000
AA: お忙しい中、丁寧なお返事ありがとうございました。
取り急ぎお礼とお願いまで。今後ともどうぞよろしくお願い申し上げます。
---------------------------------------------------------------------------------------
1331. 光起電力の円二色性
Date: Thu, 4 Sep 2014 19:06:04 +0900Q: 佐藤勝昭先生
東京大学理学部で表面物性の研究室に所属しているM1の石原と申します。
物性なんでもQ&Aのページを拝見してメールさせていただきました。
自分の所属している研究室は表面物性が専門なのですが、自分はSi薄膜などに可視レーザーを当てて生じる起電力を測るという実験をしております。
光を使った実験は当研究室にとって珍しく、基本的な光物性の知識もメンバー全員曖昧という状況です。
そこでお尋ねさせていただきたいのは、光起電力効果に円偏光依存性はあるのか、また、あるとすればそれはよく調べられた効果であるのか、ということです。
ダイオード的な振る舞いをする物質に円偏光を当てて起電力を測るというのは一見調べつくされているように感じるのですが、ピンポイントに解説した文献を見つけることができません。
勉強不足でとても基礎的なことをお尋ねしているのかもしれませんが、どうぞご教授お願い致します。
--------------------------------------------------------------------------------------
Date: Fri, 5 Sep 2014 08:09:26 +0900
A: 石原君、佐藤勝昭@新潟(ICTMC19のため出張中)です。
メールありがとうございます。光起電力に円偏光依存性が見られるかというご質問ですね。
一般的に言って,フォトダイオードなどに使われる半導体の光吸収に円偏光選択性があれば, 光起電力にも円偏光選択性が現れるのは当然です。
ではどんな場合に選択性が現れるのでしょうか?半導体の価電子帯はスピン軌道相互作用で J=3/2の状態(4重縮退)とJ=1/2(2重縮退)の状態に分裂しています。
J=3/2の量子化軸成分はJz=+3/2,+1/2,-1/2,-3/2の4状態です。
伝導帯は多くの場合、s軌道なのでJ=1/2です。量子化軸成分は、Jz=1/2,-1/2です。
ΔJz=+1の遷移(-1/2→+1/2,-3/2→-1/2)は右回り円偏光で許容です。
Δjz=-1の遷移(+1/2→-1/2,+3/2→+1/2)は左回り円偏光で許容です。
たいていの場合これらは同じエネルギーをもつので、キャンセルします。
しかし、もし、格子不整合歪みなどがあれば、キャンセルすることがなく円偏光選択性を持つのです。
たとえば、「スピン偏極電子源」の解説をお読みください。
----------------------------------------------------------------------------------------
Date: Fri, 5 Sep 2014 13:20:37 +0900
AA: 佐藤先生
丁寧な回答ありがとうございます。
おかげさまで研究を進める重要な知見と手がかりが得られました。
この度はどうもありがとうございました。
石原
----------------------------------------------------------------------------------------
1332. 断熱消磁冷却の電場バージョンはあるか
Date: Mon, 15 Sep 2014 10:16:00 +0900Q: 佐藤様
はじめまして。当方、10年ほど前に大学で物性物理(磁性理論)を専攻しており、今は全く関係のない特許関係の仕事に就いている山形直也というものです。先日あるニュースを読んで気になったことがあったため、もしご存知であればご教示頂きたくメールさせていただきました。
先日、このようなニュースがありました。
http://www.huffingtonpost.jp/science-portal/freezer_b_5812194.html
断熱消磁による冷却かぁ…講義のテスト難しかったなぁ…。なんて思って読んでいたのですが、ふと気になったことがあります。
当方の理解が正しければ、断熱消磁による冷却とは
①磁場によって強引にスピンの向きを揃えておき、エントロピーを小さく維持しておく。
②周囲から熱が入り込まないようにして磁場を切る。
③スピンの向きはバラバラになろうとするが(エントロピーは増えようとするが)、Tが稼げない。よって、吸熱(冷却)によってTをゲットし、エントロピーを増やす。
というロジックだったと思います。
ということは、強引にエントロピーが小さい状態を保った状態からそうでない状態への遷移を断熱系で行えば吸熱(冷却)は起こるということですよね?(ジュールトムソン効果もたしか同じ理屈のはず)
つまり、エントロピーが小さい状態(秩序だった状態)を維持するために磁場を利用する必然性はなく、たとえば誘電体に電場をかけてエントロピーを小さく維持して上記プロセスを実行しても冷却は可能なのではないかと思ったのです。
つきましては、
【1】 上記理屈(強いて言えば「断熱消電」)は合っているのか?
【2】 もし【1】があっているとすれば実験されたことはあるのか?
上記二点をご教示願い無いでしょうか?
以上、よろしくお願いいたします。
-----------------------------------------------------------------------------------------
Date: Mon, 15 Sep 2014 23:32:06 +0900
A1: 山形様、佐藤勝昭です。 断熱消磁による磁気冷却の原理についてのあなたのご理解【1】は、正しいと思います。
しかし、【2】誘電体の電場冷却は聞いたことがありません。おそらく絶縁破壊が起きるくらい高い電場をかけないと、常誘電体のエントロピー曲線の変化が出るほど電気双極子を揃えることができないのではないでしょうか。
私見ですが、レーザー冷却は一種の電場冷却ではないかと思います。
レーザー冷却法は、気体原子がレーザー光の電場によって生じた電気双極子により、励起光よりエネルギーの高い位相がそろった光を放出することで原子系からエネルギーが失われ、断熱状態にある原子の温度が低下しますが、原子系の温度が下がることで減少するエントロピー量と、光の電場のもつエントロピーの増加が均衡するまで冷却できるということですから、一種の電場冷却と考てもよいのではないでしょうか?
間違っているかも知れません。
-----------------------------------------------------------------------------------------
Date: Sat, 20 Sep 2014 07:47:13 +0900
A2: 山形様,佐藤勝昭です。
レーザー冷却は一種の断熱消電ではないかと書いたのですが、
首都大学東京の宮原先生から「レーザー冷却ですが、自然放出スペクトル幅の中心周波数より若干低めのエネルギーで励起するので、ドップラー効果も重要かと思われます。
エントロピーだけだと中心周波数励起でも冷却できることになりますが、実際はそうなりませんので・・・。」
というコメントをいただきました。単なる断熱冷却ではないようです。
宮原先生に、断熱消電はないかと尋ねたところ、
「 断熱消電のばあい、やはり原子核の電気双極子モーメントは非常に小さい(中性子の電気双極子モーメントはゼロと思われている)ので無理でしょうね。誘電体だと系が周りの熱浴とべったりで、断熱の条件がつくれないと思います。」とのコメントでした。
-----------------------------------------------------------------------------------------
1333. シリコンのヤング率の温度依存性
Date: Thu, 18 Sep 2014 14:30:45 +0900Q1: 佐藤勝昭 様 突然のメール申し訳ありません。私はK*大学4年生のI*と申します。大学では物理学を専攻しております。
(もしHPに掲載されるのであれば大学名名前は伏せていただきたいです。申し訳ありません。)
Siの物性値を調べていてこのHPにたどり着きましてご質問させていただこうと思いました。
今回、Siのヤング率の温度依存性を知りたいと思い調べていました。しかし、なかなかSiの機械的性質を述べた文献や論文を見つけることができませんでした。
なので、もしSiのヤング率の温度依存性に関する文献や論文、もしくはそのような実験をしている方からのデータなどをご存じであれば教えていただきたいです。
お忙しい中大変申し訳ありませんが、お時間ございましたら返事いただけると幸いです。
-----------------------------------------------------------------------------------------
Date: Fri, 19 Sep 2014 23:11:44 +0900
A1: I君,佐藤勝昭(@応物学会のため札幌出張中)です。
旅先なので手元に論文がありませんが、シリコンのヤング率の-150℃~+150℃温度依存性については
Current Applied Physics Volume 9, Issue 2, March 2009, Pages 538ー545の
Chun-Hyung Cho: Characterization of Young’s modulus of silicon versus temperature using a “beam deflection” method with a four-point bending fixture という論文に載っています.
図書館に行って取り寄せてもらってください。
-----------------------------------------------------------------------------------------
Date: Sat, 20 Sep 2014 21:32:19 +0900
Q2: 佐藤勝昭 様
早速のご返信ありがとうございました。さっそく図書館で取り寄せてもらいます。
ただ、ヤング率の温度依存性についてもう少し高い温度まで(できれば800℃ほどまで)の情報も知りたいと考えております。
もしご存知でしたら、お忙しい中恐縮ですがお返事いただけると幸いです。
-----------------------------------------------------------------------------------------
Date: Sun, 21 Sep 2014 01:31:37 +0900
A2: I君、佐藤勝昭です。
一般に、体積弾性率(bulk modulus)Bに関しては次のような温度依存性があることが示されており、これをWachmanの式といいます。
B(T)= B0 + b1 T e(T0/T)
ここに、B0は絶対0度での体積弾性率、Tは絶対温度、 b1とT0はパラメータです。
体積弾性率Bとヤング率Eの関係は、ポワソン比をνとして
E=3B(1-2ν)
です。
ほとんどの物質のBは温度に対してほぼ直線的に変化するようです。
なお、下記論文を参照して下さい。
The temperature dependence of the isothermal bulk modulus at 1 bar pressure
-----------------------------------------------------------------------------------------
Date: Mon, 22 Sep 2014 13:12:37 +0900
AA: 佐藤勝昭 様
返信ありがとうございます。
教えていただいたことを参考に少し勉強してみることとします。
お忙しい中、ありがとうございました。
-----------------------------------------------------------------------------------------
1334. 磁性体の比熱
Date: Sun, 5 Oct 2014 16:22:11 +0900Q1: はじめまして、A*大学大学院2年の、Y*と申します。
物性なんでもQ&Aのページを拝見してメールさせて頂きました。
(もしHPに掲載される場合は名前等は伏せて頂けたらと思います。)
以前から疑問に思っていたことがあり、2点質問させていただきます
①比熱
強磁性体の比熱では、磁場を大きくするとピークは高温側へシフトします。
反強磁性の比熱では、磁場を大きくするとピークは低温側へシフトしていきます。
シフトの方向が強磁性、反強磁性で異なるのはなぜでしょうか?
また、なぜピークはシフトするのでしょうか?
②低次元磁性体の比熱
低次元磁性体では、比熱において(磁化でも)山な りのピークが見られます。
山なりのピークは、低次元系の短距離秩序によることです。
ではなぜ、短距離秩序だと山なりのピークが生じるのでしょうか?
以上の2点です。
お忙しいところ恐縮ですが、どうぞよろしくお願い致します。
-----------------------------------------------------------------------------------------
Date: Fri, 10 Oct 2014 01:23:13 +0900
A1: Y君、佐藤勝昭です。
10/5に海外出張から帰ってきて、たまっていたメールを見ました。
お返事を書こうとしている矢先に、ノーベル物理学賞の日本人受賞のニュースがあってJST広報はてんやわんやの大騒ぎ、お返事が遅くなって、ごめんなさい。
私は、磁性体の比熱については、全くの専門外です。
磁界を加えると強磁性体では、ピークが高温側にシフトし、反強磁性体では低温側にシフトするということをあなたのご質問で始めて知りました。
比熱のピークはほぼ転移点付近に現れるのは知っていますが、・・
一般論でいいますと、常磁性領域ではスピンの揺らぎが大きくエントロピーが高いが、Tc以下で強磁性になると、スピンがそろうため、揺らぎが小さくなってエントロピーが低下します。
エントロピーの急な増加があるので比熱-温度曲線にピークが生じます。
常磁性体に磁界を加えるとスピンは少しずつ磁界方向にそろうので、ピークは高温側にシフトするはずです。
反強磁性の磁化率χは、ネール温度付近でピークになりますが、磁界に平行な磁化率は低温で小さくなり、磁界に垂直な磁化率は温度によらず一定です。平均するとTNより低温側で磁界によってエントロピーが低下します。これが、比熱のピークが低温側にくる原因かと思います。(ちょっと自信がありません。)
------------------------------------------------------------------------------------------
Date: Fri, 10 Oct 2014 14:56:21 +0900
Q2: 佐藤 勝昭様、A大学大学院のYです。
大変お忙しい中、ご返答誠にありがとうございます。
大変、感謝しております。
佐藤先生の比熱についてのご説明で、ピーク位置の疑問についてイメージをつかむことができました。
どうもありがとうございます。
お忙しいところ、大変恐縮ですが、もう1点ご教授頂けたら幸いです。
②低次元磁性体について
低次元磁性体では、磁化で山なりのピークが見られます。
山なりのピークは、低次元系の短距離秩序によることです。
ではなぜ、短距離秩序だと山なりのピークが生じるのでしょうか?
(実はもう1点、以前からの疑問があります。もしも差支えなければご教授頂けたらありがたいです。)
**ランデのg因子について**
g因子の値が2から大きくずれていること(帯磁率のfitting等からの導出にて)、は何を示すことが可能でしょうか?
論文によってはg値について全く触れていないものや、大きな軌道モーメントの存在や、物質の異方性を示唆しているものもあります。
ちなみに、上記の存在を示唆している理由もよくわかりません。
非常にお忙しい中、度々のご相談大変失礼致しました。
どうぞよろしくお願い申し上げます。
-----------------------------------------------------------------------------------------
Date: 2014/10/13, Mon 08:51
A2: Y君、佐藤勝昭です。
(1) 低次元系の磁気現象は専門外です。
申し訳ありませんが、小口武彦「磁性体の統計理論」(裳華房)などの書物をお読みください。
なお、1次元イジングモデルでは自発磁化は生じないと言われています。
(2)g値は角運動量と磁気モーメントの関係を表す係数です。3d遷移金属では,軌道角運動量が消失しているので、gはスピン角運動量Sと磁気モーメントμの関係の係数です。
しかし、軌道角運動量が生きている希土類などでは、全角運動量Jと磁気モーメントμの関係でなければなりません。ところがJはLとSのベクトル和なのですが、磁気モーメントに関しては
μ=(L+2S)μBなので、μとJの関係は単純ではありません。この関係を表すのがランデのg値なの です。私が、日本磁気学会誌に連載した超入門講座の第2回のpdfをお送りしますので、2.7 .4節をお読みください。
------------------------------------------------------------------------------------------
Date: Mon, 13 Oct 2014 11:08:43 +0900
AA: 佐藤 勝昭様、A大学大学院のYです。
お忙しい中度々のご返答、誠にありがとうございます。
また佐藤先生ご自身の資料も送って頂き、ありがとうございました。大変感激しております。
紹介して頂いた専門書とPDFを参考にしながら、学んでいきたいと思います。
どうもありがとうございました。
-------------------------------------------------------------------------------------------
1335. 太陽光パネルの反射
Date: Tue, 14 Oct 2014 16:22:06 +0900Q1: 佐藤勝昭 様
物性なんでもQ&Aのページを拝見してメールさせて頂きます。
私、T*大学で物理学を専攻しておりますA*と申します。どうぞよろしくお願い致します。
太陽光パネルについて勉強しておりまして、教えて頂きたい事が有りましてメールさせて頂きました。
太陽光パネル表面での入射光反射による発電ロスを抑えれば、発電量増加が見込めるのではないかというのが勉強を始めたきっかけです。
まずは実際に太陽光パネルに入射する光のエネルギーを算出しようと思ったのですが、光学に疎いため計算でつまづいてしまいました。
光のエネルギー透過率、反射率等を計算するため、フレネルの式を使用したいのですが、光の偏光(S偏光とP偏光)により使用する式が異なります。
入射光のエネルギーを100としたとき、透過光、反射光のエネルギーは○○です!と分かりやすい結果を得たいのですが、安易でしょうか?
どうぞよろしくお願い致します。
--------------------------------------------------------------------------------------------
Date: Wed, 15 Oct 2014 01:05:09 +0900
A1: A君、佐藤勝昭です。
ご質問の「太陽光パネルの表面」が何を指すのですか。
カバーしているガラスのことですか、それとも太陽電池セルの表面ですか?
セルの反射については、表面反射防止膜や表面のテキスチャー化で反射を抑えています。
カバーガラスの反射率は、あなたの仰るとおり、斜め入射の場合偏光に依存しますが、通常はそこまで考えていないのではないのでしょうか?
直入射であれば、表面反射率は R={(1-n)/(1+n)}2となります。n=1.5ならR=0.04=4%です。表面からガラス内に透過するのは、従って96%です。
セルとガラスが密着していなければ、ガラスの裏面での反射が同じく4%なので、カラス板の透過率はT=(1-R)×(1-R)=0.96×0.96=0.922=92.2%です。
もし、ガラス裏面と半導体(屈折率n0)とが密着していると、裏面反射率R'={(n-n0)/(n+n0)}2
シリコンのn0=3.7として、R'=0.179=17.9%このときセル内部に入射する光は入射光の0.96×0.821=0.884=88.4%ということになります。
このような回答でよいのでしょうか?
--------------------------------------------------------------------------------------------
Date: Wed, 15 Oct 2014 14:38:56 +0900
Q2: 佐藤様
ご回答下さいましてありがとうございました。
直入射について理解致しました。
私の説明不足に前提補填して頂きましてありがとうございます。
表面とはカバーガラスの事でございます。
もう一点質問させてください。
例えば入射角10°で入射した場合の表面反射等についてはどう計算すればよろしいでしょうか。
自然光は特定の偏光をしていないと思いますので、フレネルの式を使う際にどうすればいいのかわかりません。
どうぞよろしくお願いします。
---------------------------------------------------------------------------------------------
Date: Thu, 16 Oct 2014 10:11:37 +0900
A2: A君、佐藤勝昭です。
非偏光ということは、入射光のs偏光とp偏光の強度が同じということです。
すなわち、Is、Ipがそれぞれs偏光、p偏光の強度とすると、入射光強度Iinとすると
Is=Ip=(1/2)Iin
s、p偏光の反射率をRs、Rpとすると、反射光の強度Irは
Ir=RsIs+RpIp=(Rs+Rp)I/2
したがって、非偏光の場合の反射率は
R=(Rp+Ps)/2
としてさしつかえないでしょう。
---------------------------------------------------------------------------------------------
Date: Thu, 16 Oct 2014 10:30:12 +0900
AA: 佐藤様
ご回答頂きましてありがとうございます。
偏っているから偏光、ということですね。よくわかりました。
教えて頂きました内容で勉強を続けたいと思います。
本当にありがとうございました。
----------------------------------------------------------------------------------------------
1336. 磁場ルミネセンスはあるか
Date: Mon, 3 Nov 2014 18:55:27 +0900Q1: S県の公立中学校で理科教員をやっておりますI*と申します。ルミネセンスについて興味があり、調べています。
ルミネセンスは、励起源により、フォトルミネセンスなどの種類に分けられますが、磁場によってルミネセンスが起こることはあるのでしょうか。
多数の専門書を読んでも、記述がないので、ぜひご教授いただければと思います。
お忙しい中お手数をおかけし恐縮ですが、回答よろしくお願い致します。
なお、ウェブにこの質問が掲載される場合は、匿名でお願いいたします。
----------------------------------------------------------------------------------------------
Date: Tue, 4 Nov 2014 17:04:06 +0900
A1: I様、佐藤勝昭です。
磁場を電子にかけても、ゼーマンエネルギー程度のエネルギーしか与えることができません。
ざっくり見積もると、1テスラの磁場で電子が得るゼーマンエネルギーは0.1meVのオーダーです。
可視光の発光中心を励起するには1.7eV以上のエネルギーが必要です。従って、磁場によってルミネセンスを励起することはできないのです。
註(正確には、スピンS=1/2のゼーマンエネルギーは、E=gμBS・H=2×5.7883 × 10-5 (eV?T-1)×0.5 ×1(T)=0.05783meV~0.06meV) ----------------------------------------------------------------------------------------------
Date: Tue, 4 Nov 2014 18:10:44 +0900
Q2: 佐藤勝昭様 Iです。回答ありがとうございました。素人ゆえに教えていただきたいのですが、発光中心に1.7eVのエネルギーを磁場によってかけるのは現実的に不可能なのでしょうか?
たびたびで大変申し訳ありませんが、回答よろしくお願いいたします。
-----------------------------------------------------------------------------------------------
Date: Tue, 4 Nov 2014 21:01:47 +0900
A2: 様、佐藤勝昭です。仮にゼーマンエネルギーを0.1meVとすると、 17000テスラ(1テスラ=10000ガウス)というとてつもない磁界をかけないと ゼーマンエネルギーを1.7eVにすることができません。
地上で超電導磁石と通常電磁石の組み合わせで作れる最大の磁界は100テスラ程度です。一方、超強磁場中性子星「マグネター」は地球上でこれまでに作り出された最も強力な磁石の1000万倍の磁場を持つそうですから、強い光を出す可能性があります。
-----------------------------------------------------------------------------------------------
Date: Tue, 4 Nov 2014 21:40:53 +0900
AA: 佐藤勝昭様 Iです。とてつもなく強い磁場をかけなければ不可能なわけですね。
丁寧でわかりやすい回答、本当にありがとうございました。とても助かりました。
-----------------------------------------------------------------------------------------------
1337. ガラスのファラデー効果の測定
Date: Fri, 12 Dec 2014 06:31:24 +0000 Q1: 佐藤勝昭様はじめまして 横浜国立大3年 小澤一謹と申します。
表題の通り、ファラデー効果についてお聞きしたいことがありメールいたしました。
学校の授業で、自分でテーマを設定し調査・発表をするというものがありまして、ファラデー効果をテーマにしました。
パイレックスガラスと鉛ガラスのファラデー効果を測定しているのですが、うまく測定をすることができません。ファラデー効果について先生のHPを拝見し、助言をいただきたいです。
====================================
レーザー:λ=670nm
試料の大きさ:直径φ=6.8?8.0、長さ5.7cm
磁場:超伝導コイル(最大100000ガウス)
測定法:クロスニコル法 レーザー光を板に当て反射した光の電場強度をフォトマルで読み取り、偏向器を回しながら電場の最小値を読み取り、磁場を変え回転角を読み取ります。
====================================
この方法について良くないところはありますでしょうか。
またパイレックスガラス、鉛ガラスの670nmでのヴェルデ定数の文献値や理論式などはありますか。
この試料でファラデー効果を測定しようとするならどれほどの磁場が必要でしょうか。
-----------------------------------------------------------------------------------------------------------------------
Date: Sat, 13 Dec 2014 10:05:40 +0900
A1: 小澤一謹君、佐藤勝昭です。
確認したいことがあります。
(1)セッティングは、
(a)レーザ→偏光子→ガラス棒(超電導磁石中)→検光子→板で反射→検出器
でしょうか?それとも、
(b)レーザ→偏光子→ガラス棒(超電導磁石中)→板で反射→検光子→検出器
でしょうか?
もし(b)なら、板で反射したときに変更が乱れるので、?です。 (2)超電導磁石中に試料を置いて磁界を印加しているとのことですが
具体的な図と、磁界の加わっている部分のサイズを教えて下さい。
ご質問おベルデ定数ですが、
パイレックス 3.64×10-6 rad/(G・cm) for λ= 632 nm
[S. Egami and H. Wataria, Rev. Sci. Instrum. 80, 093705 (2009)]
鉛ガラス(60%酸化鉛の重フリントガラス)1.79×10-5 rad/(G・cm) for λ=632 nm
---------------------------------------------------------------------------------------------------------------------
Date: Sat, 13 Dec 2014 15:14:58 +0000

 Q2: 佐藤勝昭様、返信ありがとうございます。
Q2: 佐藤勝昭様、返信ありがとうございます。装置のセッティングは(a)のほうです。
図は添付したファイルにあります。拙い図で申し訳ありません。
実験では偏光の回転が見られるものの回転角は小さく、それより求めたヴェルデ定数は、
8.7×10-7[rad/G・cm]でした。
-------------------------------------------------------------------------------------------------------------------
Date: Mon, 15 Dec 2014 09:05:53 +0900
A2: 初めのメールでガラスの長さが57cmとあったのですが、図ではもっと短いようなので、本当はどうなっているのか、教えてください。
-----------------------------------------------------------------------------------------------------------------
Date: Mon, 15 Dec 2014 00:16:47 +0000
Q3: 佐藤勝昭様、ガラスの長さは5cmです。
------------------------------------------------------------------------------------------------------------------
Date: Mon, 15 Dec 2014 10:20:51 +0900
A3: 小澤君、佐藤勝昭です。
はじめの質問にあった57cmは間違いですね。
仮にベルデ定数を4 x 10-6 rad/Gcmとすると、長さ5㎝、磁界10000Gでは、約2度も回転するはずです。
偏光の回転が小さくなっている理由ですが、可能性としては、超伝導磁石はクライオスタットに入っているので、その窓材が関係している可能性があります。
そういう意味では、磁界を通常の穴あきマグネットで印加するほうがよいのではないかと存じます。
-----------------------------------------------------------------------------------------------------------------
Date: Mon, 15 Dec 2014 01:53:34 +0000
Q3: 佐藤勝昭様
角度の計算ですが、4.0×10-6×5×10000ですか。そうすると0.2[rad]、11[deg]になるのですが、 またベルデ定数が小さくなるのは温度が低いからということでしょうか。
-----------------------------------------------------------------------------------------------------------------
Date: Mon, 15 Dec 2014 11:45:09 +0900
A3: 小澤君、
ご指摘通り、2度はコンピュータ入力時のミスで約12度(11.5度)の間違いです。
常磁性のガラスの場合ベルデ定数は磁化率に比例します。磁化率は1/Tに比例するので、低温ほど大きくなります。
ガラスではありませんが、TGG(テルビウムガリウムガーネット)セラミクスの場合、ヘリウム温度では室温の値の87倍になるそうです。
(阪大ILEの年報2006)
反磁性のガラスの温度変化は小さく、変化率は10-4/Kとされています。
(Applied Optics, Vol. 30, Issue 10, pp. 1176-1178 (1991))
いずれにせよ、低温だからということはないと思います。
超伝導磁石は漏れ磁界が大きいので、フォトマルに影響を与えている可能性があります。チェックしてください。
------------------------------------------------------------------------------------------------------------------
Date: Mon, 15 Dec 2014 03:17:20 +0000
AA: 佐藤勝昭様
適切な回転角を得るためには、フォトマルが磁場の影響を受けないようにするのがよいということですね。
一度フォトマルが正常に機能するか確認してみます。
漏れ磁界を考慮し、かける磁界を小さくするか、別のコイルを探したいと思います。
----------------------------------------------------------------------------------------------------------------
Date: Sun, 18 Jan 2015 14:37:04 +0000
Q4: ??佐藤勝昭様,
お久しぶりです。横浜国立大学3年 小澤一謹です。
先日はファラデー効果についての質問にお忙しい中お答えいただきありがとうございました。
また質問がありメールしました。
漏れ磁場を考慮し、パイレックスガラスで測定したところ文献値に近い値がでました。(0.013[min/Oe・cm])
質問の内容ですが
磁場を反対方向にかけたところ反対向きに偏光面が回転したのですが、これは正しいことでしょうか。
----------------------------------------------------------------------------------------------------------------
Date: Mon, 19 Jan 2015 07:36:26 +0900
A4: 小澤一謹君、佐藤勝昭です。
漏れ磁場を考慮して測定してうまくいったのはよかったです。 ファラデー回転の正負は磁界の方向に対して定義されていますので、磁界を反転すると反転するのが正しいのです。
------------------------------------------------------------------------------------------------------------------
Date: Mon, 19 Jan 2015 02:24:01 +0000
Q5: 佐藤勝昭様
お返事ありがとうございます。
測定の正確さがましたことを言えるのでよかったです。
光アイソレーターでは磁場方向と光の方向が反転しても回転する方向が同じですが、この実験では磁場方向が変わると回転方向は逆になりました。
光と磁場の相対方向が重要ではなくて、物質の磁化方向が重要なのでしょうか。
また鉛ガラスについてですが、鉛含有率が低い透明度が低い場合はヴェルデ定数は小さくなるのでしょうか。
-------------------------------------------------------------------------------------------------------------------
Date: Mon, 19 Jan 2015 13:04:37 +0900
A5: 小沢君、佐藤です。 光の方向ではなく磁化方向に依存するのです。拙著「光と磁気(改訂版)」p10-11をお読みください。 --------------------------------------------------------------------------------------------------------------------
Date: Mon, 19 Jan 2015 07:30:25 +0000
Q6: 佐藤様
先生の本を読みました。納得できました。ありがとうございます。
また後半のヴェルデ定数の質問ですが、測定に用いたガラスの透明度が低かったのですが、
・ガラスの透明度が低いとヴェルデ定数は小さくなりますか。
それとも
・ガラスの透明度低い→光吸収大きい→楕円偏向になり光強度のピークがわかりにくい という関係はただしいでしょうか。
また鉛ガラスにおいて鉛含有率とヴェルデ定数は比例関係にありますか。
----------------------------------------------------------------------------------------------------------------------
Date: Mon, 19 Jan 2015 16:43:18 +0900
A7: 透明度とベルデ定数には、直接関係ありません。
透明度が悪い原因が不均一性や不純物、欠陥による場合、散乱などのために偏光が乱れることが考えられます。
ヴェルデ定数は鉛の濃度には比例すると思います。
-----------------------------------------------------------------------------------------------------------------------
Date: Mon, 19 Jan 2015 08:49:14 +0000
AA: 佐藤様
ありがとうございます。いい考察が書けそうです。
今回の実験を通し、あさってプレゼンをします。
先生には測定方法から原理まで様々なことについてお世話になりました。ありがとうございます。
いいプレゼンが出来るよう頑張ります。
--------------------------------------------------------------------------------------------------------------------------
1338. ナノスケール・シリコンの誘電率
Date: Wed, 31 Dec 2014 01:49:03 +0900Q1: 佐藤勝昭 様、K*大学4年生のI*と申します。大学では物理学を専攻しております。(もしHPに掲載されるのであれば大学名名前は伏せていただきたいです。申し訳ありません。)
以前にも質問させていただき、丁寧なご回答を頂戴いたしました。その節は大変感謝しております。今回も勝手ながら質問をさせていただくことをお許しください。
今回は誘電率に関する質問をさせていただきたくご連絡しました。
1、おそらく理科年表などに載っている物質の比誘電率などはある程度の大きさの試料を使い、測定していると思います。
しかし、もし試料の大きさをナノオーダー(数nm?数百nm)にすると、比誘電率の値とは変わったりするのでしょうか。また、変わるのであればどのように変化するのかなどのデータや論文はございますでしょうか。
2、同様にナノオーダーのものの比誘電率を測定するときに、真空中などで試料表面がクリーンな状態(酸化膜などがつかず、未結合手が出ている状態)で測定した比誘電率と、表面を酸化させたり、水素で終端させて測定した比誘電率では値は変わるのでしょうか。そのようなデータや論文はありませんでしょうか。
個人的には、ある程度大きなものでは表面状態などは誘電率にあまり関係はしないが、ナノオーダーのものになると表面積の割合が大きくなり、表面状態により誘電率が変化するのでは…と考えたのですがそのようなデータや論文が見つけられず困っていました。できれば、シリコンに関するような情報があれば大変うれしいです。
以上になります。 長文になってしまい申し訳ございません。
お忙しいとは存じますが、お時間ございましたら何卒ご回答のほどよろしくお願い申し上げます。
----------------------------------------------------------------------------------------------------------------
Date: Wed, 31 Dec 2014 15:01:09 +0900
 A1: I君、佐藤勝昭です。
A1: I君、佐藤勝昭です。ナノスケールにおけるシリコンの比誘電率ですか・・? あなたが言うように、バルクと比較して表面の占める割合が大きいのでバルクの誘電率とは異なるでしょうね。
これは、どのような金属を電極に付けて測定するかによって(ショットキー障壁ができるなど)case by caseになると思います。
あなたが考えている系について具体的に検討しないと、一般論では云えません。
それとは異なって、ナノスケールシリコンにおいては、バンド間励起子が量子閉じ込めを受けることによって比誘電率が減少する効果が知られています。
これは、測定条件によらないintrinsicな効果です。
荒っぽい近似によれは、比誘電率εは添付ファイルに示すように、
ε=1+A/Eg2
で表され、バンドギャップEgが大きくなると比誘電率はその2乗で小さくなります。ナノスケールの量子閉じ込め系では、量子準位がEgより高いところに出来るので、誘電率が低下するのです。
詳しくは、R.Tsu, D.Babic, L.Ioriatti: Simple model for the dielectric constant of nanoscale silicon particle; Journal of Applied Physics Volume 82 Issue 3 1327 - 1329 (1997)をお読みください。
------------------------------------------------------------------------------------------------------------
Date: Wed, 31 Dec 2014 16:08:49 +0900
AA: 佐藤勝昭 様、K大学 Iです。
お忙しい中大変申し訳ございません。丁重な対応、心より感謝申し上げます。お教えいただいた内容を参考に勉強してみます。
----------------------------------------------------------------------------------------------------------------
1339. CrやTiドープのAl2O3の蛍光について
Date: Mon, 26 Jan 2015 12:21:27 +0900Q: 佐藤先生
メイルにて失礼致します。私は、A独立行政法人にて機能材料研究を行っております研究員Fです。
最近、専門外の無機蛍光体の特性に関心を持ち、試行錯誤をはじめたところなのですが、文献検索を含め自分の調査では分からないところがあり、ネット検索にて先生のHPを拝見し、恐縮ながらご質問させて頂いている次第です。
CrやTiドープのAl2O3に関する下記の点について、もしご教示を頂ければ大変有り難く存じます。
1)CrドープAl2O3(ルビー)は700nm近傍に強い発光を示す(裾を含めると室温での発光範囲は660-740nmくらいでしょうか?)ことは多くの文献で報告されており、先生の公開されていらっしゃられる資料でも触れられていますが、私どもがCrのドープ量を変化させたサンプルを調製している中で、750nmよりも長波長側にも蛍光ピークを示すものが見つかりました。
(我々のサンプル調整法は微粉末を混合し、焼結する方法です。)
長波長側の蛍光に関して調べたのですがそのような報告を見つけることがまだできていないのですが、もし上述のような現象についてご存知でいらっしゃられましたらご教示を頂きたくお願い致します。
(そのサンプルに特異的に発生した何らかの条件(結晶の歪みなど)、あるいは、他の不純物の混入なども含め原因を考えているところではありますが、いかんせん専門外のため手間取っております。)
2)レーザー媒質として活用されているTi:Sapphireの粉末状試料を得るべく、1)同様に、Ti2O3をAl2O3に適量混合し焼結させましたが、文献で報告されているようなブロードな蛍光スペクトル(650-950nm以上)は得られず、むしろ、CrドープAl2O3に非常に近い蛍光スペクトルが観察されました。この理由が分かりません。コメントをいただければ幸甚です。
3)上述のTi:Sapphireもそうですが、レーザー媒質を蛍光材として活用することはあまり無く、蛍光材は蛍光材として別途材料系が探索され、実用化されているように思われるのですが、その理由はどういうものでしょうか?
以上、長文になりましたが、よろしくご教示頂ければ幸甚です。どうぞよろしくお願い致します。
---------------------------------------------------------------------------------------------------------
Date: Mon, 26 Jan 2015 14:58:30 +0900
A: F様、佐藤勝昭です。
メールありがとうございます。さて、ご質問ですが、私の知識の範囲でお答えします。
(1)RubyのR線より長波長側に現れる発光は、Cr-Cr対発光です。
Cr3+イオンの濃度が1%程度となると,結晶中のCr3+イオン対が無視できないほどの数になり、吸収スペクトルや、発光スペクトルにイオン対による対スペクトル(pair spectrum)が現れます。
R1線の発光スペクトルは6943Åに現れますが、対発光スペクトルのうちN1線は7040Å、N2線は7009Å(77K)にあらわれます。長波長に現れる原因は交換相互作用によるエネルギーの低下です。
例えば、磁性体ハンドブック(朝倉書店, 1975)p1029を参照してください。
(2)Ti3+は3d電子を1個しか持たないので、Cr3+のR線のような多電子系特有のスピン禁制遷移による鋭いスペクトル線ではなく、基底状態2T2, 励起状態2Eの間のスピン許容の遷移で、基底状態、励起状態ともに、非常にエネルギー的に接近した多数のバイブロニック準位(フォノンと結合した電子準位)が存在し、バイブロニック準位間の遷移を選択することでレーザ作用を起こしています。
したがって、鋭い発光線が観察されたとすれば、不純物の可能性があります。
ブルーサファイアはFe2+とTi4+の間の電子移動でFe3+とTi3+が生じるような吸収帯が赤~緑の波長域にあり、このため青く見えているのですが、この過程でできたFe3+の多電子状態間の遷移が鋭い発光線をもたらす可能性があります。ルビーと同様のスペクトルだとすれば、Cr3+が混じっていた可能性もあります。
(3)レーザーで用いるためには、反転分布を作る必要があるので、3準位レーザの場合、上の励起準位は許容、下の励起準位は禁制であるようにするのが普通です。
ルビーでレーザにおいて励起するための遷移は4A2-->4T2の許容遷移、発光する遷移は2E-->4A2の禁止遷移です。したがって、弱励起でキャビティのない普通の蛍光体の場合、レーザ用材料は光らないので使い物にならないのではないでしょうか?
---------------------------------------------------------------------------------------------------------------
Date: Mon, 26 Jan 2015 17:40:58 +0900
AA: 佐藤先生;
この度はお忙しい中、当方の質問に対してご丁寧かつ詳細なご回答を頂き有難うございました。
Q1。については、Cr-Cr対発光の帯域よりも遥かに長い所に振動構造を持つ比較的ブロードな(室温測定においてですが)蛍光が見られているので、これは何か予期しない原因が混在していると考えるべきと理解致しました。
引き続き検討を続けてみたいと存じます。
Q2。は、乳鉢での調製時など、Crが混入した可能性を含め再検討してみたいと存じます。
Q3。は、ご説明を伺い、疑問が解消致しました。
この度は誠に有難うございました。
---------------------------------------------------------------------------------------------------------------
1340. 半導体のドーピングとラマンスペクトル
Date: Fri, 30 Jan 2015 15:17:41 +0900Q: 佐藤勝昭 様
初めまして。T*大学4年生のH*と申します。
このたびホームページを拝見し質問させて頂くことになりました。なお、お手数ではございますが、Webに掲載の際には大学名、氏名ともに匿名にてよろしくお願いいたします。
私は希土類であるイットリウムをケイ素にドープさせた物質について研究しております。
そこで、
①イットリウムは価電子を3つ持つためP型半導体(または、P型半導体に似た挙動)を形成するのでしょうか?
②また、こちらの論文によると、顕微ラマン分光を用いた際に、レーザーパワー密度によってラマンのシフトダウンの度合いがP型半 導体、N型半導体、ケイ素の単独で、異なるということが書かれています。
(PHYSICAL REVIEW B 73, 245309 (2006)のFig4部分です。pdfにて添付しますのでご確認ください)
シフトダウンを生じる要因はどのようなものがあるのでしょうか?
お忙しいなか申し訳ありませんが、ご教授頂けるとありがたく存じます。それではよろしくお願いします。
-------------------------------------------------------------------------------------------------------------
Date: Fri, 30 Jan 2015 23:50:47 +0900
A: H君、佐藤勝昭です。
4年生ということですが、卒論でしょうか?卒論での疑問については、原則として指導教員に尋ねるべきです。
匿名希望ということなので、何か聞けない事情があるのでしょうね。
以下のことをヒントに、勉強して下さい。
①もし、YがSiサイトを置換すれば、あなたの言うようにアクセプタになるはずですが、3価のイットリウム(Y3+)のイオン半径は約100pm(=1Å), 4価のシリコンのイオン半径は 約40pm(=0.4Å)なので、Siの原子位置を置換するのは困難です。
YをSiにドープしようとしても、置換位置に入らず、格子間原子(interstitial)として入ったり、無理に置換すると、隣のSiが空孔(vacancy)となり、Yと空孔の対をつくって深い準位をつくります。(ドナーにもアクセプタにもならない) GaAsに希土類之Er3+をドープするには、微量の酸素を導入して、Ga-O-Erという形にするそうです。
希土類はoctahedral siteを好むのでSiのようなtetrahedral siteには入りにくいようです。
②についてですが、添付のPhysical Reviewの論文を読みました。
Siナノワイヤのラマンピークのレーザ強度依存性がundoped, P-doped, B-dopedで異なるという内容ですね。
RESULTS AND DISCUSSIONの一番最初にラマンピークの低エネルギーシフトの原因には、4つあるとして、
(1)レーザ光の吸収による温度上昇、(2)高いキャリア密度、(3)量子閉じ込め効果、(4)Siナノワイヤのストレス を挙げています。
Conclusionでは、(1)と(4)がダウンシフトの主因で、(2),(3)はあまり考えなくてよいようです。
私はJSTさきがけ「次世代デバイス」の研究総括をしていたのですが、その一期生にNIMSの深田直樹研究者がいて、 B-doped Siナノワイヤのラマンによるキャリア活性化を研究しており、ラマン線のFano効果を使って、Bをドープしたときの形状解析からキャリア密度を推定していました。またBに局在したフォノンによるラマンピークも見つけていました。
N. Fukata: "Impurity doping in silicon nanowires ", Adv. Mater. 21 (27), 2829-2832 (2009).
が参考になるでしょう。
あなたの卒論テーマは、「Yを添加したSiの顕微ラマンによる評価」なのですか?
顕微ラマンの解釈は、4年生にはかなり高度の研究内容ですね。先生に聞けないのなら、あなたの研究室の先輩の大学院生に教えてもらいなさい。
-------------------------------------------------------------------------------------------------------
Date: Sat, 31 Jan 2015 17:17:20 +0900
AA: 東京農工大学名誉教授
佐藤 勝昭 様
こんにちは!
昨日は多忙であるにもかかわらず迅速かつご丁寧に対応して頂きありがとうございました。
卒論テーマは少し異なるのですが、評価の一部に顕微ラマン分光を用いた測定を含んでいるといった次第です。
佐藤様よりご提示頂いた深田さんの論文を熟読し、自身の卒論に活かしていきたいと思います。
この度は誠にありがとうございました。
---------------------------------------------------------------------------------------------------------
1341. 金の酸化物の作製について
Date: Sun, 1 Feb 2015 15:12:35 +0900Q: 佐藤 勝昭 様、初めてご連絡させていただきます。
HPを大変興味をもって拝見させていただいております妹尾と申します。
化学には特別な知識はございませんが、貴金属に興味を持つ者でございます。
早速でございますが、「金の化学的性質として一般的に酸素とは直接、高温でも化合しない」。と多くの書籍、化学辞典に書かれております。
ところが、先日、無機化合物・錯体辞典(講談社)の中に酸化金Au2O3の製法の一つに、金線を酸素中で熱する。との記載がありました。
Au2O3は、不安定で250℃で酸素と金に分解、生成エンタルピーも+19,100 (cal/mol)でAu単体のほうが安定であり、熱力学的にも高温ほど 分解する方向に反応が進むのではないかと認識いたしておりました。
上記製法は、どのように理解すればよいのか。知識不足のため、お手数ではございますがご教授いただければ幸いでございます。
よろしくお願いいたします。
------------------------------------------------------------------------------------------------------------
Date: Sun, 1 Feb 2015 19:52:43 +0900
A: 妹尾様、佐藤勝昭です。
バルクの金を酸素中で高温に加熱しても金を酸化することはできません。
しかし、ナノメートルサイズの金粒子や直径がナノメートルサイズの金線では、 金結晶の原子配列の段差(専門用語ではステップといいます)のところに酸素 が物理的吸着(adsorption)することが確認されています。
結晶面によって吸着の程度は異なり、(111)面より(211)面のほうが活性が強いとされます。
これによってCOを酸化してCO2にするための触媒として金のナノ粒子が使われます。
Kingという研究者は、空気中で紫外線を当ててオゾンを作ることで金の表面に17 ± 4Å厚のAu2O3皮膜が出来ていることを確認しています。
(D.E. King, J. Vac. Sci. Technol. A. 13 (1995) 1247)
Koslowskiという研究者は酸素プラズマ中で40Åの酸化物が出来ると報告しています。
(B. Koslowski,et al., Surf. Sci. 475 (2001) 1.)
従って、金のナノワイヤを高温の酸素プラズマ中で処理すればAu2O3が出来ると考えられます。
(J. Kim et al. / Surface Science 600 (2006) 4622-4632を参考にしました。)
----------------------------------------------------------------------------------------------------------
Date: Sun, 1 Feb 2015 22:42:59 +0900
AA: 佐藤 勝昭 様
ご教授いただきました妹尾でございます。
ご多忙のところ、早速のご返信ありがとうございます。
当該表現がナノスケール条件下での反応ということで理解いたしました。
佐藤先生、ご教授いただき本当にありがとうございました。
----------------------------------------------------------------------------------------------------------
1342. 複素誘電率とクラウジウス・モソッティの式
Date: Thu, 19 Mar 2015 14:03:38Q: 佐藤先生
はじめて連絡させていただきます。
T*社のK*と申します。
物性の扱いについて行き詰っていたところ、HPを拝見し連絡させて頂きました。
HP掲載の際には社名・氏名ともに匿名でお願いします。
複素誘電率について質問させてください。
現在、Clausius-Mossottiの式を用いて誘電率から分極率を算出しようとしています。
その際に、複素誘電率を式に代入する場合はどのようにすれば良いのか悩んでいます。
計算では分極率を実数で得たいと考えています。
代入は複素誘電率の実部のみとするか、虚部を含めて絶対値とするか、複素数のまま代入して計算後に実部のみを取るか、その他の方法などご教示お願いします。
浅学なため、見当違いな質問かもしれませんが、よろしくお願い致します。
-------------------------------------------------------------------------------------------------------
Date: Fri, 20 Mar 2015 00:51:56
A: K様、佐藤勝昭です。
クラウジウス・モソッティの式は、複素誘電率に対しても成立します。
分極率も一般に複素数です。なぜなら、分極Pとは、電界Eを加えた後に 媒体の電気双極子が変化する様子を与えているので、当然、応答に遅れ が生じますが、この遅れを表現するのが虚数部だからです。
光に対する分極などは、複素数で扱うべきですが、電気泳動の際の 泳動力を求めるような場合は、実数部のみが意味を持ちます。分極率を 何に使うかによるのではないでしょうか。
分極率の実数部を求める場合は、複素誘電率を式に代入し、計算後 実数部をとって下さい。
電気泳動法についての複素誘電率については添付の文献をご参照下さい。
Rom. Journ. Phys., Vol. 59, Nos. 7?8, P. 862-872, Bucharest, 2014
---------------------------------------------------------------------------------------------------------
Date: Fri, 20 Mar 2015 10:34:02
AA: 佐藤先生
早速のご返信ありがとうございました。
大変参考になりました。
これからもHPを参考にさせていただきます。
---------------------------------------------------------------------------------------------------------
1343. fAより小さな電流の測定法
Date: Wed, 25 Mar 2015 15:11:46Q: こんにちは、お世話になっております。L社のH申します。
早速質問させていただきますが、 最近 Oxide TFT(IGZO)の漏洩電流(off-state Current)にかかわった測定をしていますが、 通常の半導体パラメター測定器(例;HP4156など)ではフェムトアンペア(fA)程度が 装置の精度制限らしいですね。
IGZOの漏洩電流はfAよりはるかに下回(10^-21A程度という論文もありますね)っていて、通常の測定器では正確な測定が困難であると痛感しています。
そこでいろんな文献を探ってみると外部キャパシタンスを利用した測定など{Kiyoshi Katoら、JJAP 51(2012)021201}の間接的な方法で 測定可能だと存じておりますが、他に低レベルの電流測定を直接に可能にする測定装置や方法があるとご意見お伺いしたいです。
何卒よろしくお願いいたします。
-------------------------------------------------------------------------------------------------------
Date: Thu, 26 Mar 2015 06:51:46
A: H様、佐藤勝昭です。
メールありがとうございます。MOSの専門家にも聞いたのですが、測定器として市販されている ものは、fAが限度であるということです。H様が紹介された論文は、電荷が長時間にわたって保持 されていることから、間接的にリークがyA以下だと推定して、メモリに使えることを述べている ものです。fA以下になると、空気中からのリークだって問題になるので、有効な測定法はないと 思います。お役に立てず申しわけありません
-----------------------------------------------------------------------------------------------------
Date: Thu, 26 Mar 2015 21:05:17
A2: H様、佐藤勝昭です。 Facebokで質問を紹介したところ次のようなコメントがありました。
宮原 恒昱(首都大学東京名誉教授)
微小電流計の初段のOPアンプ内部のFETのゲート漏れ電流がすでに室温で10fAくらいあります。差動増幅でキャンセルするよう にしていますが・・・・。マイナス21乗アンペアは、電子1個が100秒に一回くらい通過するくらいですから、光電子分光のような、 ある種の計数測定が必要かと思います。それでもバックグラウンドを考えると簡単ではありません。
山口 政紀 (東陽テクニカ)
素子を集積して並列につなぐ。サンプルを真空中に置いて余計なリークを防ぐ。計測器の電荷Q測定のモードで長時間積分する。温度を上げて わざとリークを増やす。などいかがでしょう。
-------------------------------------------------------------------------------------------------------
Date: Fri, 27 Mar 2015 10:21:10
AA: 佐藤先生
親切なお返事、どうもありがとうございます。 -21乗という数値は論文で見た情報で、われらの測定(おそらく、FacebookでCommentされたCoulombmeter測定と同じ方法だと思いますが、 TFTのSource端子にキャパシタンスをつないで、そのキャパシタンスに変化する電圧計ることでQを推測する方法
参照:keithley社提供Low level measurements handbook2-3-8章)では Width 1μm当 10-16~10-18程度でした。
TFTのwidth を大きくしたり、測定時の温度を高くする方法など、いろいろ方法で測定器の制限より高い値になるような方法でクロスチェックをした結果です。
Engineering観点では、サブFemtoレベル(-15乗~-1 8 乗 )の電流が上記の方法(時間を沢山かけて蓄積されるQをはかる測定)ではなく 電流の値が直接、瞬時で測れたらより効率的ではないかと思った上での質問でしだが、やはり直接はかるのは無理らしいですね。
計れる方法をより効率化する事を考えていきます。再度、ご意見どうもありがとうございました。
--------------------------------------------------------------------------------------------------------
1344. 自然光学活性について
Date: Mon, 30 Mar 2015 17:11:18Q: 佐藤先生
お久しぶりです。以前にも質問させて頂いた京都大学の古賀と申します。
その節は大変丁寧に質問にお答え頂き、ありがとうございました。
今回は自然光学活性について質問させて下さい。
佐藤先生の著書「光と磁気」で勉強し、磁気光学効果とは単純には外部磁場で磁区が揃った上での スピン軌道相互作用による準位の分裂と、左右円偏光の軌道量子数に関する選択則によるものである、 との解釈に至りました。
ここで疑問なのですが、酒石酸水溶液などの磁場を必要としない円二色性はどのように説明できるのでしょうか?
感覚的には鏡像対称な構造によるものだと理解していますが、量子力学的な説明はできないでしょうか?
また磁気光学効果においても疑問があります。磁気円二色性の原因がスピン軌道による準位の分裂なら、
電子遷移の場合だけ起こって、格子振動の起こる波長範囲では円二色性は起こらないのでしょうか?
以上2つの疑問についてお答え頂けると幸いです。よろしくお願いいたします。 -----------------------------------------------------------------------------------------------------------
Date: Wed, 1 Apr 2015 00:07:18 +0900
A: 古賀様、佐藤勝昭です。
メールありがとうございます。
(1) 自然旋光性および円二色性(CD)を合わせて光学活性と呼びます。
光学活性を持つ結晶の典型は水晶です。α水晶では、光軸方向に 伝搬する直線偏光は旋光性をもちます。Kramers-Kronigの関係から α水晶も吸収端付近にCDを示します。
水晶を構成する原子の配列状態に右回りのらせんがあることが 右水晶の旋光性の原因とされていますが、原子配置から旋光性を 説明するには至っていないと、小川智哉「結晶物理工学」(裳華房 1976)p.209に書かれています。
しかし、最近の研究では
Mark P. Silverman: Quantum Superposition--Counterintuitive Consequences of Coherence, Entanglement, and Interference (Springer, 2008)Section 7.6 (p299)によれば、
光学異性体のようなキラルな物質においては、電気双極子遷移と 磁気双極子双極子遷移を同時に起こし、光の固有状態は、右回り および左回り円偏光となり、その位相速度に差が生じる。
と書かれています。
さらにノーザン・イリノイ大学のNorma Greenfield先生の授業資料 の Origins of optical activity. の(p6)によれば、
遷移の旋光性は、電気双極性光のよって誘起された電気双極子と 磁気双極子の内積の虚数部で表される。RK=Im(uek・umk) RKがゼロでない値を持つための条件は、次の3つである。
(1) 同じ発色団に電気双極子・磁気双極子の2つの遷移が存在する場合
(2) 2つのグループがそれぞれ単一の電気双極子をもち、それがカップルして磁気双極子をつくる。
(3) 1つの分子に2つの発色団があり、1つが磁気双極子で、もう1つが電気双極子である場合。
量子力学で光学活性を説明するのは難しい。下記文献を参照せよと書かれています。
C.R.Cantor,P.R. Shimmel, Biophysical Chemistry Part II,( W.H. Freeman and Co., NewYork, 1980.)
----------------
(2) 格子振動と光の相互作用は、電子遷移ではないので、スピンが関与しませんから磁気光学効果は起きないと思います。
------------------------------------------------------------------------------------------------------------------------
Date: Sat, 4 Apr 2015 17:58:39 +9:00
A2: 古賀様、佐藤勝昭です。
分子系の自然光学活性の量子論については、多くの量子化学系の論文や書籍があるようです。
図書館に行って、調べてください。
Dietrich Haase: On the quantum mechanical theory of natural optical activity; Theoretica Chimica Acta 64, 421 (1984)
R. Guy Woolley: On the Optical Activity and the Molecular Hypothesis; Structure and Bonding Volume 52, 1982, pp 1-35
Magdalena Pecul and Kenneth Rund: The ab Initio Calculation of Optical Rotation and Electronic Circular dichroism;
Advances in Quantum Chemistry Volume 50, pp.185-212 (Elsevier , 2005)
------------------------------------------------------------------------------------------------------------------------
1345. 真鍮板の反りについて
Date: Thu, 21 May 2015 17:27:28 +0900Q: 佐藤勝昭様、突然のメール申し訳ありません。W社Oとと申します。
ネットで検索をしていて物性なんでもQ&Aにたどり着きました。
質問内容
私は仕事で真鍮板(1.2mmと3mm厚)を第二塩化鉄液で腐食(腐食深度480μm)して 印刷用の凸版を製造しているのですが、仕上がった版が反ってしまいます。
長年そのまま作業をしておるのですが、何とか反りを解消したいと思っております。
是非ともご意見を伺いたいです。
よろしくお願い致します。
--------------------------------------------------------------------------------------------------------------------------
Date: Fri, 22 May 2015 08:16:50 +0900
A1: 様、佐藤勝昭です。
メールありがとうございます。お困りのようですね。同業他社も同じ悩みなのでしょうか、 それとも御社のみの問題なのでしょうか。
私は凸版印刷について知識がないのでもう少し詳細な情報を下さい。真ちゅう版の厚み、面の寸法、エッティングの深さ、凸版エッチング時の条件など。
---------------------------------------------------------------------------------------------------------------------------
Date: Fri, 22 May 2015 20:21:09 +0900
Q2: 佐藤勝昭様、W社Oです。
ご返事ありがとうございます。説明不足で申し訳ありません。
詳細といたしまして、
材質:真鍮
厚み/サイズ:1.2mm厚/400mm×365mm 3.0mm厚/450mmx365mm
エッチングの深さ:1.2mm厚/0.53mm 3.0mm厚/1.2mm
です。
エッチング行程ですが、
生の真鍮板にスピンコーターにてレジストを塗布
↓
その上にネガフィルムを密着
↓
UV露光装置で露光
↓
現像
↓
370℃オーブンにてバーニング
↓
エッチング行程
・版裏に黒ワニス塗布
・表面を第二塩化鉄液で肌出し
↓
エッチングマシーンにて腐食
○第二塩化鉄液に添加剤を混ぜた溶液を吹き付けて腐食
○塩酸で洗浄
○キリン血を非腐食の土手部分に付着させる(横からの腐食防止)
○370℃オーブンでバーニング(1min)
○冷却
※○の5工程を腐食時間を変えて繰り返す。(1.2mm厚は5回 腐食時間1min,2min,3min,5min,7min)
(3.0mm厚は7回 腐食時間1min,2min,3min,5min,7min,10min,12min)
後は版洗浄して断裁です。
金属凸版腐食では、弊社は亜鉛と真鍮の実績が有りますが、どちらも反りが生じますので、同業他社も同じ問題を抱えていると思われます。
現在は手等で反りを戻して納品しておりますが、不完全で何とかできないかと思っております。
よろしくお願い致します。
----------------------------------------------------------------------------------------------------------------------
Date: Fri, 22 May 2015 23:38:24 +0900
A2: O様、佐藤勝昭です。
詳細な情報ありがとうございます。
エッチング前の平坦な真ちゅう板を370℃に加熱後室温に冷却しても加熱・冷却が均一なら反りは生じないはずです。
エッチングした部分では冷却が早く、バルク側は冷却が遅いので、応力のちがいから塑性変形が起き、反るのではないかと思います。
1.2mm厚の真ちゅう板に深さ0.53mmのエッチングをして370℃の加熱・室温への冷却を5回も繰り返すのですから
加熱・冷却の速度のちがいで何らかの塑性変形が起きるでしょう。
解決方法としては、加熱・冷却が均一に起きるようにするとか、現実的ではないけれど、上下を厚い金属ではさみ、強い力で押さえつけて変形を起こさなくするなどが考えられます。
------------------------------------------------------------------------------------------------------------------------
Date: Mon, 25 May 2015 11:14:29 +0900
AA: 佐藤 勝昭様, お世話になります。W社のOです。
ご連絡ありがとうございます。加熱・冷却の均一化を図ってみたいと思います。
大変助かりました。ありがとうございます。
-------------------------------------------------------------------------------------------------------------------------
1346. 励起子吸収がある場合の(αhν)2プロットによるバンドギャップ推定
Date: Mon, 29 Jun 2015 14:51:46 +0900^2 plot sample1.png) Q: 佐藤勝昭様 突然のメール申し訳ありません。私はN*大学 4年のH*と申します。
Q: 佐藤勝昭様 突然のメール申し訳ありません。私はN*大学 4年のH*と申します。(もしHPに掲載されるのであれば大学名名前は伏せていただきたいです。申し訳ありません。)
物性なんでもQ&Aのページを拝見してメールさせていただきました。
私は薄膜太陽電池の光吸収層の研究をしております。
現在、とある試料の透過率T、反射率Rから吸収係数aを計算し、(αhν)2プロットよりバンドギャップを算出しようとしております。
しかし、励起子吸収(?)が大きく発生しており(添付図)、バンドギャップを求めることができませんでした。
このようなプロットからバンドギャップを求めるにはどのような処理を施せばよいのでしょうか?
お忙しいところ申し訳ありませんが、 ご教授願えたら幸いです。 よろしくお願いします。
------------------------------------------------------------------------------------------------------------------------
Date: Tue, 30 Jun 2015 23:21:19 +0900
A. H君,佐藤勝昭です。多忙のため、お返事が遅くなってごめんなさい。
励起子吸収がバンド間遷移に重なっている場合は、励起子吸収スペクトルを ローレンツ型の吸収曲線で近似して、それとバンド間吸収スペクトルとを足し合わせて もとの吸収曲線にフィッティングするのがよいと思います。
[ローレンツ曲線については、花村栄一「固体物理学」(裳華房)参照:この本では分極率をαで表記していますから注意!]
ローレンツ型の複素誘電率ε(ω)=ε'(ω)+iε"(ω)のスペクトルは
ε(ω)=1+4π(Ne2/m*)Σn(fn/(ωn2-ω2-iγω)
複素誘電率εと屈折率nと消光係数κの間にはε=(n+iκ)2 が成り立ち、
[これについては、佐藤・越田「応用電子物性工学」(コロナ社)第3章参照]
ε'=n2 - κ2, ε"=2nκ
吸収α(ω)は複素誘電率の虚数部に次式で関係します。
α(ω)=2ωκ/c=ωε"/c
パラメータとして(Ne2/m), γ、fnを適当に選んでフィットしてみて下さい。
------------------------------------------------------------------------------------------------------------------------
Date: Wed, 1 Jul 2015 11:14:02 +0900
AA: ご返事ありがとうございます。
さっそく試してみたいと思います。
お忙しい中、丁寧にご教授いただきありがとうございました。
-------------------------------------------------------------------------------------------------------------------------
1347. 誘電体内部での電磁波エネルギー収支について
Date: Thu, 20 Aug 2015 09:22:19 +0000Q: 佐藤先生、T*社 A*と申します。
初めてメールさせて頂きます。お世話になります。
「物性なんでもQ&A」を見て、メール致しました。大変失礼ですが、匿名にてお願いいたします。
浅学の為、光学の計算で良く分からない点が有ります。虚数部を持つ屈折率の誘電体内部での電界とエネルギーの関係式について教えて頂けないでしょうか?
空気から誘電体への反射率,透過率は、
r0=(1-n-ik)/(1+n+ik), t0=2/(1+n+ik)
誘電体から空気への反射率,透過率は、
r1= - (1-n-ik)/(1+n+ik), t1=2(n+ik)/(1+n+ik)
になるかと思います。
ここでエネルギー保存なのですが、
(1) 空気から誘電体の場合は、
|r0|^2={(1-n)^2 + k^2}/{(1+n)^2 + k^2}=1-4n/{(1+n)^2 + k^2}
|t0|^2= 4 /{(1+n)^2 + k^2}
実数の例で良く見かける様に単純に、|t0|^2に誘電体の屈折率の実部(n/1)を掛ければ解決するのですが、
(2) 逆の誘電体から空気の場合は、
|r1|^2={(1-n)^2 + k^2}/{(1+n)^2 + k^2}=1-4n/{(1+n)^2 + k^2}
|t1|^2= 4{n^2+k^2} /{(1+n)^2 + k^2}
強引に答えを合わせようとすると、|t1|^2に誘電体の屈折率の実部/絶対値2乗を掛けなければいけなくなります。
本来それぞれ、(屈折率の絶対値/1), (1/屈折率の絶対値)を掛ける事が、物理的に正しそうに感じます。
安直なイメージですが、そもそもこの2つの係数は掛けて1にならないと、誘電体内部を伝播する光のエネルギーが定まらないと思えます。
私の理解したかった関係式は、
入射波のエネルギー=反射波のエネルギー+透過波のエネルギーから
|1|^2 = |r|^2 + α|t|^2
(αは入射側媒体と透過側媒体間での電界強度を補正する係数。
入射側媒体の屈折率をn0, 透過側媒体の屈折率をn1とした場合、α=n1/n0と思われます。)
が成り立つと思っているのですが、そもそもこの考え方に問題が有りそうでしょうか?
お忙しいところ、申し訳有りません。
よろしくお願いいたします。
以上
---------------------------------------------------------------------------------------------------------------------
Date: Mon, 24 Aug 2015 14:31:59 +0900
A: A様、佐藤勝昭です。
入射側では、反射波と入射波が干渉しているので、界面でのエネルギー保存は
[入射波と反射波の干渉波]のエネルギーと透過波のエネルギーが保存されることになります。
界面においては電界の連続性から
E0+rE0=tE0が成り立ちます。
1+r=tが成り立つので
1=t-rとなり、絶対値の2乗について1=|t-r|^2が成立します。
これを書き直すと、
1=(t*-r*)(t-r)=|t|^2+|r|^2-Re(t*r+r*t)
干渉項Re(t*r+r*t)は必ずしも|t|^2に比例しないので
|1|^2 = |r|^2 + α|t|^2
は必ずしも成立しないと思います。
----------------------------------------------------------------------------------------------------------------------
Date: Mon, 24 Aug 2015 05:52:10 +0000
AA: 佐藤先生
T社 Aです。いつもお世話になっております。
早速のご回答有難うございました。
干渉項Re(t*r+r*t)はかならずしも|t|^2に比例しないので
はい、突き詰めるとこの干渉項が邪魔している為
、 |1|^2 = |r|^2 + α|t|^2
が成り立たなくて困っていました。
そもそも、この関係式が成り立つという考えを改めるべきの様ですね。
考え直してみたいと思います。
お忙しいところ、お時間を割いて頂き有難うございました。
以上
----------------------------------------------------------------------------------------------------------------------------
1348. 仕事関数制御についての質問
Date: Fri, 21 Aug 2015 21:09:56 +0900Q: 佐藤勝昭様 突然のメール失礼致します。 H*大学M1のM*と申します。(匿名希望) 先生のHPを拝見し、連絡させていただきました。研究テーマは、MOSFET等のデバイス作成です。 質問の内容は、仕事関数の制御についてです。 仕事関数について勉強している中で、PtやAu等の化学的に不活性な金属の仕事関数が高いことを知りました。 これらの仕事関数の値は、酸化物系にはおよびませんが、合金化や表面処理で、電子状態を変化させ バナジウム酸化物のような高い値を得ることは、物理的に可能なんでしょうか。 よろしくお願い致します。 --------------------------------------------------------------------------------------------------------------------------------
Date: Sun, 23 Aug 2015 21:41:49 +0900
A: M君、佐藤勝昭です。
仕事関数には、バンド構造だけでなく、表面の電子状態が関わるので複雑ですが、合金化によって制御できます。
MOSのメタルゲートのための仕事関数制御は、(国研)物質材料研究機構(NIMS)の知京主任研究者のグループで取り組んでおられます。
NIMS now Vol.5 (2006)
Pt-Wの合金を作って仕事関数の変化を確認しておられます。知京豊裕さんに直接お尋ねになってはいかがでしょう?
-----------------------------------------------------------------------------------------------------------------------------------
Date: Mon, 24 Aug 2015 21:15:01 +0900
AA: 佐藤勝昭様
H大学 Mです。
ご回答ありがとうござます。
頂いたURLを確認しました。
組成の変化で、仕事関数を制御することが可能とのことなので実際に作成してみようと思います。
ありがとうございました。
-----------------------------------------------------------------------------------------------------------------------------------
1349. アクリルゴムの熱膨張係数について
Date: Mon, 24 Aug 2015 14:27:41 +0900Q: 佐藤勝昭 様
初めまして。F**大学修士1年のO*と申します。
このたびホームページを拝見し質問させて頂くことになりました。
なお、お手数ではございますが、Webに掲載の際には大学名、氏名ともに匿名にてよろしくお願いいたします。
現在私は、電圧を印加することで膨張するアクリル系エラストマーを使用したアクチュエータを製作しています。
また、それに伴い有限要素解析を行う予定なのですが、電圧による膨張率を測定することは非常に困難であるため、 電圧による膨張率を熱膨張率と置き換えて解析することになりました。
しかし、メーカーに問い合わせた結果アクリル系エラストマーの熱膨張率はわからないとのことでしたので、 アクリルゴムの熱膨張係数を使用しようと考えています。
しかし、知識不足のためアクリルゴムの熱膨張係数がわからず、ご教授願いたいと思い連絡しました。
自らの未熟のためにお手数おかけしますが、何卒よろしくお願いいたします。
-----------------------------------------------------------------------------------------------------------------------------------------
Date: Mon, 24 Aug 2015 21:15:01 +0900
A: O様、佐藤勝昭です。
アクリルエラストマーを用いた人工筋肉アクチュエータは、誘電体に電界を加えることによって、 Maxwellの応力で膨張が起きる現象を利用します。
そのメカニズムは
メリーランド大学マイクロテクノロジー研究室のホームページ
を参考にしてください。
また、 R. Pelrine, R. Kornbluh, Q. Pei, and J. Joseph, Science, 287:836-839 (2000)
によれば、100%を超える膨張が報告されています。
熱膨張ではこんなに大きく膨張することはありませんから、参考にならないと思います。
原点に立ち返って、参考文献を読んで、誘電応力の大体の大きさを見積もってはいかがですか?
研究室の指導教員や先輩学生ともよく話し合ってください
参考文献: (1) Ron Pelrine, et al.: Dielectric Elastomer Artificial Muscle Actuators: Toward Biomimetic Motion; Proc. SPIE 4695, Smart Structures and Materials 2002: Electroactive Polymer Actuators and Devices (EAPAD), 126 (July 10, 2002)
(2) Nguyen Huu Chuc et al.: Artificial Muscle Actuator Based on the Synthetic Elastomer; International Journal of Control, Automation, and Systems, vol. 6, no. 6, pp. 894-903, December 2008
-----------------------------------------------------------------------------------------------------------------------------------------------
Date: Tue, 25 Aug 2015 00:40:47 +0900
AA: 佐藤勝昭 様
F大M1年のOと申します。夜分遅くに失礼します。
返信ありがとうございます。
確かに熱膨張では大変形を生み出すことができないため、有限要素解析においても参考にならないですね。
参考文献を読み直して、おおよその見積もりを出してみます。
参考文献の添付までしていただきありがとうございます。
お忙しい中、ありがとうございます。
失礼いたします。
------------------------------------------------------------------------------------------------------------------------------------------------
1350. AlGaAsはGaAsよりAs抜けが起きやすいか?
Date: Tue, 1 Sep 2015 11:53:31 +0900Q1: 佐藤先生、はじめまして。私はD*社のS*といいます。
(所属・氏名は匿名でお願いします。)
赤外LEDのp型不純物の拡散工程について質問させてください。
弊社が製造しているLEDは点光源が特長で、大小様々なサイズの発光部が 光るチップ構造になっており、発光部(層)はAlGaAsです。
(製造工程の詳細な記述を省略:佐藤)
1バッチあたりの発光部の総面積が小さいケースで発光部にダークスポット が発生しやすい傾向がみられます。
(製造工程の詳細な記述を省略:佐藤)
この状況を説明するため
「GaAsに対してAlGaAsからのAs抜けの速度が極端に速く、発光部 の総面積が小さいほうは、Asの飽和蒸気圧に到達するまでの時間が余計に かかるためAs抜けを助長し、結晶欠陥の発生を促す。」
という仮説を立てました。
この現象を論理的に説明する何か良いアイデアはないでしょうか?
----------------------------------------------------------------
Date: Tue, 1 Sep 2015 17:05:32 +0900
A1: S様、佐藤勝昭です。
お困りであることは理解できますが、ご質問の内容がなんでもQ&Aの趣旨である一般性がなく、 個別の技術相談ですので、お答えしかねます。また、質問内容はオープンにしますので、 たとえ匿名でも、プロセスのノウハウが明らかになります。従って、なんでもQ&Aとしてはお答え できません。
なお、ヒントですが、ダミー基板を使い回していると、ダミー基板上に 堆積したp型ドーパントのため、LED上のドーパント濃度が高くなり 過ぎていることが考えられます。ダークスポットはヒ素抜 けでなく、過剰ドーパントということは考えられないでしょうか?
------------------------------------------------------------------
Date: Wed, 2 Sep 2015 08:24:50 +0900
Q2: 佐藤先生、早速の返信ありがとうございます。 質問の内容が一般性がないとのことですが、ひとつだけ教えてください。 AlGaAsとGaAsを真空容器中で加熱した場合、Asの分解速度に 差が生じる可能性はありませんか?両物質とも私が探した資料の中に飽和 蒸気圧のデータが見当たらず過剰pドーパントの件はともかく、同一条件下での 発光部面積の大小の差違を説明するためにもアドバイスをよろしくお願い します。
-------------------------------------------------------------------
Date: Sat, 5 Sep 2015 20:05:44 +0900
A2: S様、佐藤勝昭です。
お返事が遅くなり申し訳ありません。
実は、東京農工大学の熊谷先生にメールでAs蒸気圧について問い合わせておりました。
このほど熊谷先生から次のような見解が示されました。
----------------------------------------------
難しい内容で中々良い答えが有りませんが、私も先生と同じく、ダミー基板の 汚染が原因でpドーパントの影響が出ているのではと思います。
念のため、600℃でのAlAsとGaAsの分解の平衡定数を計算してみました。
AlAs(s) = Al(s) + 0.5As2(g) K=8.49E-10 @600℃
GaAs(s) = Ga(l) + 0.5As2(g) K=4.86E-6 @600℃
よって、GaAsよりもAlAsの方がずっと安定で、「GaAsに対してAlGaAs からのAs抜けの速度が極端に速く、…」という推察は成り立たないのではと思 います。
------------------------
以上ですが、このQ&AをWebにアップしてもよいでしょうか?
-------------------------------------------------------------------
Date: Mon, 7 Sep 2015 08:20:11 +0900
AA: 佐藤先生、お手を煩わせて大変恐縮です。
pドーパントの影響については一度実験で確認したいと思います。非常に参考になりました。
Q&A掲載の件ですが、最初の質問は先生のご指摘通り、内容に公開したくない部分が 多々あるため遠慮させて頂きたいと思いますが、2つ目の質問については匿名を条件に 掲載していただいてもかまいません。いろいろお世話になりました。
(これを受け、Q1の製造工程の詳細な記述を省略して掲載しました:佐藤)
--------------------------------------------------------------------------
1351. 水の配向とフォノンの関係(ハイパーラマン散乱)
Date: Thu, 1 Oct 2015 05:17:04 +0000Q1: 佐藤勝昭 様
HPを拝見しました.私K*大学M1のY*と申します(webにアップする場合は匿名でお願いします.)
お忙しいと思いますので、お時間よろしければ教えて下さい。
私の研究室での論文紹介で私に渡された液体の非線形光学の論文で分からないことがあり,研究室の先生も専門分野ではなく分からないため質問させて下さい.
Citation: The Journal of Chemical Physics 141, 224506 (2014);doi: 10.1063/1.4903541 View online: http://dx.doi.org/10.1063/1.4903541
という論文です.(私の研究室の先生方は液体の長距離秩序に興味があると思われます.)
この論文では重水(D2O)に1064nmの入射光(レーザー光)をいれ,532nm(with spectral bandwidth 60cm^-1)の散乱光強度を複数の角度で四つの偏光角度で測定しています.それを論文中の式でフィッティングしています。
ここで質問ですが、(1)これはレイリーウィング散乱と見ていいでしょうか?
もしそうだとして、(2)レイリーウィング散乱とはどの様な物理的な運動に起因するものでしょうか?
一応調べた範囲では、「配向を持った分子の方向が,熱揺らぎのため振動をしており、それによる散乱。」 ということらしいですが、物理的なイメージがつかめません。
この論文では、最終的に水に配向があると結論づけているのですが、どうしてそうなるかが分からず、 レイリーウィング散乱が鍵になっているのではないかと予想しています。
また(3)配向がある理由がmolecular rotation-translation coupling in acoustic phononによるといっていますが、 これに関してもよく分かりません。
以上の点について、もしよければ何か教えて下さい。
ちなみに、自分なりに非線形光学の入門書を関係ありそうなところは読んだので、 最低限の非線形光学の知識はあるつもりです。
参考文献も半分くらい読む努力はしました。
しかし、液体中のphononが出てくる話は不慣れで、配向とacoustic phononとどういう関係があるのか つかめませんでした。
化学物理を研究しておりますので、物理系の院生くらい物理を知っている前提で、 容赦ない回答をいただけると嬉しいです。
----------------------------------------------------------------------------------------------------------
Date: Thu, 1 Oct 2015 18:42:50 +0900
A1: Y君、佐藤勝昭です。 Nevada大学のDr.David Sheltonは、非線形光学を用いた偏光ハイパー・レーリー散乱の専門家です。
下記の論文を読んで見てください。
Philip Kaatz and David P. Shelton: Polarized hyper‐Rayleigh light scattering measurements of nonlinear optical chromophores; J. Chem. Phys. 105, 3918 (1996)
Philip Kaatz, Elizabeth A. Donley and David P. Shelton: A comparison of molecular hyperpolarizabilities from gas and liquid phase measurements; J. Chem. Phys. 108, 849 (1998)
Philip Kaatz and David P. Shelton : Polarized hyper-Rayleigh light scattering measurements of nonlinear optical chromophores; J. Chem. Phys. 105, 3918 (1996)
David P. Shelton: Hyper-Rayleigh scattering spectrum of liquid nitromethane; J. Chem. Phys. 123, 111103 (2005)
David P. Shelton: Are dipolar liquids ferroelectric? J. Chem. Phys. 123, 084502 (2005)
----------------------------------------------------------------------------------------------------------------
Date: Thu, 1 Oct 2015 12:08:41 +0000
Q2: 佐藤勝昭様
お返事ありがとうございます.
返信遅くなってしまいすいません.
早速読んでみます.
Shelton教授はその道では有名な方だったのですね.
---------------------------------------------------------------------------------------------------------------------
Date: Fri, 2 Oct 2015 11:32:29 +0000
Q2': 今読んでいる論文
David P.Shelton: Long-range orientation correlation in water; J.Chem.Phys. 141,224506 (2014)
の式(1)?(4)の導出が記述してある文献を送ります.
これも,もし必要でしたら参考にして下さい.
David P. Shelton: Polarization and angle dependence for hyper-Rayleigh scattering from local and nonlocal modes of isotropic fluids; J. Opt. Soc. Am. B/Vol. 17, No. 12/December 2000
David P. Shelton: Nonlocal hyper-Rayleigh scattering from liquid nitrobenzene; The Journal of Chemical Physics 132, 154506 (2010)
それから,現時点での私の理解を述べます.
ある大きさのdomainのある運動モード(polar collective modeと記述あり)がtranverseな方向に伝わっており,配向をなしている.
その運動はtranslation-rotation couplingな運動をしている.運動が波のように伝わっているのでacoustic phononと呼んでいる.
疑問としては,運動のモードが実際にはよく分からない,という点です.あと,自分の理解にも自信が持てません.
この理解に関してもコメントいただけると嬉しいです.
よろしくお願いします.
----------------------------------------------------------------------------------------------------------------------
Date: Sun, 4 Oct 2015 01:54:30 +0900
A2: 君、佐藤勝昭です。
私は、液体の構造に土地勘がないので、long-range orientation・・のポイントになる部分を訳してみました。
(添付ファイル)
従来、水をはじめとする液体は、分子配向はランダムで、長距離配向はないと考えられていましたが、非線形光学HRS の解析から長距離の配向秩序が見出され、シミュレーションと矛盾しないというのが、この論文の主旨ですね。
分子の配向の揺らぎ(回転)と分子の運動(変位)が結合して全体として極性をもつ領域(ドメイン)があって、 縦波の分極波が伝わるだけでなく、横波の分極波も伝わるモードがあるのだと思います。
-----------------------------------------------------------------------------------------------------------------------
Date: Tue, 6 Oct 2015 02:49:42 +0000
Q3: 佐藤勝昭様,Yです.
和訳に労力を割いていただき恐縮です.ポイントや大筋がはっきりしました.ありがとうございます.
まだ細かいところで質問させて欲しいのですが,ランダムな分布をしている液体の場合SHGはないですが, 今回の場合,ランダムな配向からの散乱の寄与も考えています.
私には矛盾しているように思われます.つまり,ランダムな配向からの散乱がなく,秩序を持った配向からの散乱のみになるはずです.
何か勘違いしていると思いますがこの点についてどう考えればよいでしょうか?
何度もすいません.よろしくお願いします.
-------------------------------------------------------------------------------------------------------------------------
Date: Tue, 6 Oct 2015 14:50:28 +0900
A4: Y君、佐藤勝昭です。 局所モードのHRSはhyperpolarizability μa(2ω)=(1/4)βabc Eb(ω)Eg(ω)
とEの2次で与えられるので、ランダムであっても中心対称が存在しなければ、ゼロにならないはずだと思います。
---------------------------------------------------------------------------------------------------------------------------
Date: Tue, 6 Oct 2015 06:14:53 +0000
Q5: 佐藤勝昭様,Yです.
素早いお返事ありがとうございます.恥ずかしい質問ですが,「ランダムで中心対称性が存在しない,」
とはある瞬間にスナップショットをとってその瞬間には中心対称性がない場合もあるという意味でしょうか?
----------------------------------------------------------------------------------------------------------------------------
Date: Thu, 22 Oct 2015 10:21:28 +0900
A6: Y君、佐藤勝昭です。 お答えが遅くなってごめんなさい。
私も自信がなかったので、液体の非線形光学がご専門の 埼玉大学工学研究科応用化学専攻の山口祥一教授にお伺いしました。
先生からのお返事は、
「液体は一様等方でSHG不活性のはずなのに,ハイパーレイリー散乱が観測されるのはなぜか,というお話だったと思います.
電話で先生も仰っていた通り,2倍波を出す双極子のベクトルをそのまま液体全体で足し上げてしまうとゼロになってしまいます
(SHG不活性)が,各分子からの散乱光は双極子の自乗ということで,それを足し上げたものがハイパーレイリー散乱ということになろうかと思います.
このあたりの話を簡潔にまとめたものは,残念ながら見当たりませんでした.どうもすみません.」
ということでした。
--------------------------------------------------------------------------------------------------------------------------------
Date: Fri, 23 Oct 2015 00:19:04 +0000
AA: 佐藤勝昭様,Yです.
お返事ありがとうございます.他の先生にも質問して下さりありがとうございます.
「分子のモーメントのゆらぎ」ですか.直感的に納得できます.
佐藤先生に助けてもらい理解がとても進みました.
ボランティアでやっていただいているのに大変失礼ですが,まだよく分からないこともあります.
(どういう集団運動を仮定して理論式を得たのか,集団モードからの散乱とはどういう物理現象なのか,分子の対称性とP,Rは関係あるのか) 次にこの問題と出会った時により深い理解をしようと思います.
いろいろご教授頂き本当にありがとうございました.
P.S 佐藤先生の著書「理科力を鍛えるQ&A」を最近読み始めました.知らないことがたくさん書いてあり面白いです.
----------------------------------------------------------------------------------------------------------------------------------
1352. 全反射と金属の反射のちがい
Date: Thu, 29 Oct 2015 10:03:03 +0900Q1: はじめまして。突然のメール、失礼致します 。
HPをみてメールさせて頂いております.
私は、S*社の平本と申しまして、現在、LEDデバイスの設計を担当しております。
HPに載せる際は、社名のみ匿名にして頂ければと思います。
===============================
光の挙動について色々と事実索していたところ先生のWEBサイトにたとりつきこの度メールさせて頂きました。
素人質問で大変恐縮ではございますがこ教授頂ければ幸いです。
質問はAgの反射率iについてです.下記のように理解しておりますがこの認識で間違いないのか確認させて頂ければと思いました。
または根本的な部分についても、事象がこんがらがってしまいましたので、系統立ててご教授頂ければと思いました。
お忙しい中.お手数ですがよろしくお願いします。
私の認識は、反射には大きく2種類有るが.Agの反射特性は①ではなく② に依る.というものです。
①屈折率差に起因する全反射(スネルの法則に基づく)
②自由電子による遮蔽による反射(屈折率は関係なし)
一方、根本的なところで考えると、②の特性は誘電率で決まる。
複素屈折率も誘電率で決まる。
金属の複葉屈折角は複素屈折率で決まる。
金属の反射率も複素屈折率で決まる(金属において1-反射率=吸収率になる?)
このように考えると.①と②は相関がある為、実は②の振る舞いは①に含まれる。
すなわち複素屈折角を正しく求めると結果、どの角度から光が入射しても全反射の挙動になるのでは?となり
先の認識と相反してしまいました。
質問の背景ですが、(幾何光学で光線の振る舞いを計算する)シミュレーションソフトにおいて
従来は面にAgの反射率特性を与えておりましたが、Agの屈折率を調べたところ0.15前後だった為
実は屈折率差に起因する全反射によるものなのか?いや、それだと空気⇒Agでは垂直入射の光が
(スネルの法則を適用した場合は)屈折してしまい、実際の挙動と合わない・・・というような混乱によるものです。
===================================
最後に、このようなサイトを立ち上げ、広く門戸を開けて下さり、心より感謝申し上げます 。
以上、宜しくお願い致します。
--------------------------------------------------------------------------------------------------------------------
Date: Thu, 29 Oct 2015 11:11:35 +090
A1: 平本様、佐藤勝昭です。
金属の高い反射率は基本的には複素誘電率の実数部ε'が負になることによります。
ε'=n^2-κ~2なので、消光係数κが屈折率より大きいことが負のε'の原因です。
あなたは、消光係数のことを考えていなかったので混乱したのだと思います。
なお金属の反射と色については添付の解説(トライボロジスト誌)をお読み下さい。
屈折率と誘電率の関係については、添付の書籍コピー(機能材料のための量子工学)を参考にして下さい。
--------------------------------------------------------------------------------------------------------------------------
Date: Thu, 29 Oct 2015 11:29:13 +0900
Q2: 佐藤様、早々のご返信、真にありがとうございます 。
まずは送付頂いた添付ファイルを熟読致します。
その後、まだ答えに確信がもてなかった場合は、再度質問をさせてください。
取り急ぎ御礼のみ。
--------------------------------------------------------------------------------------------------------------------------
Date: Thu, 29 Oct 2015 12:09:41 +0900
A2: 平本様、佐藤勝昭です。
資料を読んでいただくとして、ご質問に一応お応えします。
全反射と金属の反射はインピーダンス不整合という点では同じですが、機構が別だと 考えて下さい。
全反射は、単に屈折率の大きな媒体から小さな媒体に光が進むとき臨界角を超えると 伝搬光は伝わらないで近接場光のみ存在するという現象です。
一方、金属のプラズマ周波数以下での高い反射率は、角度によらず起き、金属の吸収 が大きいために金属の表面で吸収されてできた電気双極子がアンテナとなって直ちに 光を放射することによって起きるのです。各双極子からの放射は干渉し合って、反射 の法則で決まる方向に反射するのです。(このようなミクロな機構は本に書いてあり ませんが・・)
---------------------------------------------------------------------------------------------------------------------------
Date: Thu, 29 Oct 2015 16:35:56 +0900
AA: 佐藤様 資料拝読いたしました。
完全に理解しきれた・・・とは言い切れないまでも当初の疑問については解消されました。
改めて勉強ができて楽しかったです 。
ありがとうございました。
----------------------------------------------------------------------------------------------------------------------------
1353. 磁性微粒子の高周波特性
Date: Fri, 18 Dec 2015 10:33:45 +0900Q1: 研究開発戦略センター フェロー 佐藤様
いつもお世話になっております。以前、磁性材のセミナーでご講演を拝聴させていただきましたA社Oと申します。その節は、大変お世話になりました。
突然のご連絡にて大変恐縮ですが、磁性粉体について、ご教示いただきたいことがございます。
渦電流を抑えるために、粒径を小さくすることが有効と聞いております。
一方で、表皮効果という理論も有るようで、整理したいです。
------------------------------------------------------------------------------
教えていただきたいことは、
1、 渦電流の発生メカニズムはどのようか?抑えるには、どうしたら良いか?
2、 表皮効果はどのような現象か?表皮効果が発生しているときの磁束はどのようになっているのか?
3、 「高周波中の磁性粉は、表皮に近い部分のみ磁性があり、中心部は磁性が無くなる」と聞いたことがあります。これも渦電流もしくは表皮効果が影響しているのでしょうか?
御回答いただけますと幸いでございます。
御手数おかけいたしますが、御検討お願い致します。
------------------------------------------------------------------------------------------------------------------------
Date: Fri, 18 Dec 2015 15:01:29 +0900
A1: O様、佐藤勝昭です。
メールありがとうございます。
1、 渦電流の発生メカニズムはどのようか?抑えるには、どうしたら良いか?
金属に変化する磁界を印加すると、変化を打ち消す様な磁界を発生させようとして、
渦状の電流が流れる現象です。電気抵抗率が高ければ、渦電流は流れません。
酸化物などとのナノグラニュラー構造を作って抵抗を高めます。
2、 表皮効果はどのような現象か?表皮効果が発生しているときの磁束はどのようになっているのか?
表皮効果は、電磁波が媒体の中に入って減衰することによっておきます。表皮深さは
δ=(2/σ'ωμ0)^(1/2)で表されるので、導電率の実数部が大きいと短くなります。
静磁場の磁束については関係ありません。
3、 「高周波中の磁性粉は、表皮に近い部分のみ磁性があり、中心部は磁性が無くなる」と聞いたことがあります。これも渦電流もしくは表皮効果が影響しているのでしょうか?
私は、そのようなことを聞いたことがありません。
「中心部は磁性が無くなる」というのは、内部にまで高周波磁界が入らないので、
中心部からの磁気共鳴の応答がなくなるということをいっているのではないでしょうか?
なお、ナノ微粒子軟磁性体の高周波特性については、
電気学会編「ナノ構造磁性体ー物性・機能・設計」共立出版2010.6.25刊 第2章を参考にしてください。
------------------------------------------------------------------------------------------------------------------------------------------------
Date: Fri, 18 Dec 2015 19:00:31 +0900
Q2: 佐藤様、早速のご返信ありがとうございます。また、ご丁寧な解説に感謝いたします。
「内部にまで高周波磁界が入らない」とは、渦電流などで磁界が減衰(ジュール熱へ変換)していき到達しないことを指しますでしょうか?
それとも、そもそも磁界が入らないと理解したら良いでしょうか?不勉強で申し訳ございません。
ご提案の著書も確認致します。
------------------------------------------------------------------------------------------------------------------------
Date: Fri, 18 Dec 2015 21:44:44 +0900
A2: O様、佐藤勝昭です。 表皮効果の式は
E=E0 exp(-iωt) exp{i(ωμ0σ/2)1/2z} exp{-(ωμ0σ/2)1/2z}
と表され、exp{-(ωμ0σ/2)1/2z}の形で減衰します。
高周波磁界も同じ形で減衰します。
これは、仰るとおり、まさに、ジュール熱へ変換が起きているのです。
-------------------------------------------------------------------------------------------------------------------------
Date: Mon, 21 Dec 2015 15:50:52 +0900
AA: 佐藤様, Oです。
いつもお世話になっております。勉強させていただき、誠にありがとうございます。
お忙しい所、丁寧にご回答いただき感謝いたします。
今後ともよろしくお願い致します。
--------------------------------------------------------------------------------------------------------------------------
1354. プラズモンの電場増強効果とステンドグラスの色
Date: Fri, 18 Dec 2015 19:04:48 +0900Q1: こんばんは、初めまして。T**大4年K**です。
HPを拝見させていただき、ご連絡差し上げました。
局在表面プラズモンの光に対する性質について理解できないことがあります。
是非おしえていただけたらと思います。
局在表面プラズモンは、その金属ナノ粒子に対応する共鳴波長(または振動数)を吸収することで 電場増強効果を発揮するということを学びました。
この電場増強効果を用いて、共鳴波長を持つLEDの発光効率を強めることができるとのことでした。
また、もう一つ、ステンドグラスで応用されている原理を調べました。
ガラス中の金属ナノ粒子が共鳴波長を吸収して透過させなくなり、代わりに共鳴波長を持つ色の補色が見えるようになるとのことでした。(例えば共鳴波長が緑色の領域なら赤が見えるようになり、緑は透過しない)
このことを踏まえると、上記の、プラズモンを利用してLEDの発光を強めるというのは、LEDの光を吸収し透過しないので不可能なのではないかと考えてしまいました。
もしくは逆に、共鳴波長の発光効率を上げることができるならば、ステンドグラスは共鳴波長の色に見えるのではないかと。
何か勘違いがあるように思いますが、教えてください。
----------------------------------------------------------------------------------------------------------------------------
Date: Sat, 19 Dec 2015 01:12:24 +0900
A1: さん、佐藤勝昭です。
4年生ということは、卒業研究ですか?卒研での疑問は、本来指導教員に聞くべきものですよ。
ヒントを差し上げましょう。
ステンドグラスの場合は、ガラスの誘電率と金属プラズモンの誘電率の重み付き平均による実効誘電率になっています。
このような実効誘電率の取り扱いをMaxwell-Garnett近似といいます。
この場合は、エネルギーの集中効果を使っていません。
一方、ナノメートルサイズの金属粒子に光を照射すると粒子表面に表面プラズモン共鳴が励起され、 光のエネルギーが粒子表面に集中する効果が得られます。このように光を制御する効果をもつ金属 のナノ構造はナノアンテナと呼ばれます。表面プラズモン共鳴の電場集中効果によりナノアンテナ の周囲では照射した励起光の強度が高くなり蛍光体に光が集中し強く励起されるのです。ナノアン テナは光を特定の方向に回折し、外部に放出する役目を果たすたします。
------------------------------------------------------------------------------------------------------------
Date: Sat, 19 Dec 2015 12:26:45 +0900
Q2: Kです。早速のご回答ありがとうございました。
佐藤先生のおっしゃる通り卒業研究の内容であり、この疑問は指導教員に聞くべきものでした。
指導教員の考え方が理解できないので、佐藤先生にご意見いただければと思いました。
ご返信いただいたことで、ステンドグラスと電場増強では別の現象が起こっていることがわかり、とてもすっきりしました。
詳しいことはまた調べてみようと思います。感謝いたします。
また、
増強したい光の波長を吸収するようなプラズモンをLED上に作ればLEDの発光強度は大きくなる可能生がある。
透過率は電場増強にはあまり関与しないとの見解のもと実験を行っていますが、不安になりました。
私の考えの勘違いはどういった点でしょうか。
------------------------------------------------------------------------------------------------------------
Date: Thu, 24 Dec 2015 16:14:10 +0900
A2: さん、佐藤勝昭です。
プラズモンによるLEDの光増強を研究しておられる岡本先生に伺いました。
先生の見解は以下の通りです。参考にして下さい。
===============================================
「金属微粒子による局在表面プラズモンを利用する場合、励起波長とプラズモン共鳴波 長が重なれば増強しますが、発光波長と重なる場合は、金属微粒子のサイズによって 吸収断面積と散乱断面積が異なりますので、その比によって消光か増強かのどちらかが起きます。
従って、小さい微粒子の場合は吸収が増強される場合が多く、逆に大きめの微粒子の場合はプラズモン が集めた光を散乱するので、発光増強できるということだと思います。」
------------------------------------------------------------------------------------------------------------
Date: Fri, 25 Dec 2015 14:04:49 +0900
AA: 佐藤勝沼先生
T*大学のK*です。
お忙しい中、別の先生に確認などしてくださりありがとうございます。
突然連絡をしたにも関わらずこのような対応をしていただけたことに、 大変感銘を受けております。
岡本先生のプラズモンの本は何冊か拝見しており、岡本先生にまでご意見を頂けて嬉しい限りです。
そして想像以上に金属表面プラズモンによる電場増強が難しいということがわかりました。
ここ最近の疑問がそういうことだっかのかと、納得できました。
ありがとうございました。
佐藤先生の質問コーナーを通じて多くの知識を得ることができたことに感謝申し上げます。
多岐に渡り丁寧な回答をどうもありがとうございました。
より一層卒論研究に励みたいと思います。
------------------------------------------------------------------------------------------------------------
1355. 炎色反応の記述
Date: Wed, 23 Dec 2015 09:00:12 +0900Q1: はじめまして。福田と申します。某企業で化学系の専門職を長年勤め、現在は退職して無職です。
「基礎から学ぶ光物性」 (第9回第1部ルミネッセンスとは)を見て、一つ疑問があります。6枚目のスライドに、
(1) 原子が光る→炎色反応 原子は高温に熱せられると、熱励起により励起状態になった原子が基底状態に 戻るときに特有の色の発光をする性質があります。これを「炎色反応」と呼びます。
という記述がありますが、Cu、Ca,、Sr等の炎色反応の色は、原子スペクトルの色ではなく、塩化銅、塩化カルシウム、 塩化ストロンチウムに起因する分子スペクトルの色と思うのですが、いかがでしょうか?
----------------------------------------------------------------------------------------------------------------------------------
Date: Wed, 23 Dec 2015 09:27:06 +0900
A1: 福田様、佐藤勝昭です。
メールありがとうございます。Wikiでは、「高温の炎中にある種の金属粉末や金属化合物を置くと、 試料が熱エネルギーによって解離し原子化される。それぞれの原子は熱エネルギーによって電子が励起し、 外側の電子軌道に移動する。励起した電子はエネルギーを光として放出することで基底状態に戻り、この際に 元素に特徴的な輝線スペクトルを示す。」
となっています。原子スペクトルと考えてよいでしょう。
----------------------------------------------------------------------------------------------------------------------------
Date: Thu, 24 Dec 2015 23:38:44 +0900
Q2: 佐藤先生
早速のお返事をいただき、ありがとうございます。
実は、私は定年退職後、初心に帰って高校の化学教科書を復習しており、今、炎色反応をいろいろ調べています。Cu、Ca、Srの炎色反応の色について、輝線スペクトル(原子スペクトル)ではなく、バンドスペクトル(分子発光)に起因するのではないかと思ったのは、インターネットで次のような記述を見たからです。
「炎色反応により放出される光には、主に3種類ある。1つには、線スペクトルで特定の波長のところにでてくる多数の純粋に近い単色光からなり、その形状が多数の細い線からなるスペクトルである。2つ目は、連続スペクトルで分光器の分解能を上げても分解されずに連続的に現れるスペクトルである。3つ目は帯(おび)スペクトルで分子の与えるスペクトルである。原子のそれのように線ではなく、幅を持った帯状のスペクトルである。
スペクトルの中でたくさんのスペクトルが集中している部分をバンドスペクトルという。この光の特徴は原子やイオン、固体から出るのではなく、気体分子、特に二原子分子から放出される点にある。2500℃ほどの温度で発色させるには好都合であり、花火にはもちろん炎色反応で見られる鮮やかな色の部分はこのバンドスペクトルであると考えられる。」
また、別の記事には、表-1に、「Cu (炎色:緑、波長:537.0nm (CuOH)), Ca (炎色:赤黄、波長:622.0nm (CaOH)), Sr (炎色:紅、波長:605.9nm (SrOH))」 という記述がありました。
アルカリ金属の炎色は確かに 輝線スペクトル(原子スペクトル)ですが、アルカリ土類金属やCuはどうも バンドスペクトル(分子発光)が主因のような気がします。インターネット情報で怪しい面もありますが、もう少し調査してみたいと思っています。
今後とも、ご指導のほどよろしくお願いします。
-----------------------------------------------------------------------------------------------------------------------------
Date: Fri, 25 Dec 2015 07:24:09 +0900
A2: 福田様、佐藤勝昭です。
ご指摘いただきありがとうございます。
私は、話を簡単にするため、輝線スペクトルのみを扱いましたが、 たしかに気体分子から発光している発光帯がありました。
資料に注意書きを入れたいと存じます。
------------------------------------------------------------------------------------------------------------------------------
1356. 金の透過光について
Date: Wed, 23 Dec 2015 23:06:00 +0900Q1: 佐藤 勝昭 先生
はじめまして。
私は高校で化学を教えております山本喜一です。
この度、金がなぜ金色をしているのかを調べておりましたら、先生の「金属の色と金属光沢」に巡り合い、大変勉強になりました。
次に疑問に思っているのは、薄い金箔が青い透過光を示す原因についてです。
金箔に光を当てた場合、550nmよりも長波長側の光はプラズマ振動によって反射され、550nmよりも 短波長の青い光は5d→6s間のバンド遷 移に使われて、最終的に熱になってしまうのであれば、 青い透過光は生じないはずだと考えております。
どのような仕組みで、金箔が青い光を透過させるのかをご教授いただければ、幸いです。
----------------------------------------------------------------------------------------------------------------------------
Date: Thu, 24 Dec 2015 10:40:05 +0900
 A1: 山本先生、佐藤勝昭です。
A1: 山本先生、佐藤勝昭です。PalikのOptical Constants of Solids Vol.1 p294に掲載されている金の消光係数kのスペクトルを元に吸収係数αを
α=4πk/λ
の式で計算し、これに基づき厚さd=20nm=200Åの金薄膜の透過率T(%)を
T=exp(-αd)*100
として計算しました。
添付図の様に透過率のピークは4900Å(青緑)付近にあり、短波長側(青側)は緩やかに低下し、長波長側(緑側)は急激に低下しています。
このため、目には青の成分が強く入り、青っぽく見えるのでしょうね。
---------------------------------------------------------------------------------------------------------------------------
Date: Thu, 24 Dec 2015 21:12:25 +0900
Q2: 佐藤 勝昭 先生
お忙しいところ、早速のご返信ありがとうございます。
不勉強で申し訳ありません。
先生に計算していただいた透過光のスペクトル分布は、プラズマ振動や5d→6Sバンド間遷移とはどのような関係があるのでしょうか?
ご教授いただければ幸いです。
よろしくお願いします。
--------------------------------------------------------------------------------------------------------------------------
Date: Thu, 24 Dec 2015 23:00:39 +0900
 A2: 山本先生、佐藤勝昭です。
A2: 山本先生、佐藤勝昭です。添付の図は、Cu, Ag, Auの誘電率のスペクトルです。
厳密な意味で誘電率の実数部が2-5eVで0を横切るのはAgだけです。
Auにおいて2eVより低エネルギーのε"のスペクトルは自由電子による Drude吸収のすそです。
> ---------------------------------------------------------------------------------------------------------------------------
Date: Fri, 25 Dec 2015 08:58:33 +0900
AA: 佐藤勝昭 様、山本です。
お忙しいところいろいろと教えていただき、ありがとうございました。
大変勉強になりました。
---------------------------------------------------------------------------------------------------------------------------
1357. 複素誘電率について
Date: Thu, 31 Dec 2015 17:26:31 +0900Q: 佐藤勝昭先生
HPを拝見させていただきました。K*大学4年生のT*と申します。Webへ掲載する名前は匿名でお願いいたします。
誘電率及び複素誘電率について質問させていただきたく存じます。
複素誘電率は一般的に
ε=ε1+iε2 ・・・ (1)
の形で表されるのは様々な教科書に書かれているかと思います。
一方で、ネットや文献で物質の誘電率を調べると特定の実数値(例えばガラスであれば4.0など)で表記されています。
これは、上式の(1)と矛盾しないのでしょうか?
もしくはこのように文献値に示される実数値は、ε1なのかε2なのか、|ε|なのか、はたまたこれとは別のεのことなのでしょうか?
いろいろ調べていくと、デバイ型の誘電率では、ε(∞)やε(0)という値が出ることがわかったのですが、これらの値のことなのでしょうか?
私の誘電率に関する理解が間違っている部分があればご指摘いただければと思います。
お手数おかけいたしますが、ご回答いただければ幸いです。
----------------------------------------------------------------------------------------------------------------------------
Date: Thu, 31 Dec 2015 19:00:25 +0900
A: 君、佐藤勝昭です。
複素誘電率の実数部が普通の誘電率です。虚数部は、誘電損失を表す物理量です。
キャパシタ(コンデンサ)の場合、その容量を決めているのは誘電率の実数部です。
コンデンサの損失を決めているのが誘電率の虚数部です。コンデンサに使う誘電体の性能(悪さ)を表すために誘電正接tanδ=ε"/ε'が使われます。
誘電率も誘電正接も周波数依存性があります。京セラの誘電体のカタログによれば、1MHzにおける比誘電率、誘電正接が下の表のように載っています。
| 材質 | 比誘電率 | 誘電正接(10-4) |
|---|---|---|
| アルミナ(Al2O3)A445 | 9.8 | 20 |
| イットリア(Y2O3)Y100A | 11 | 5 |
| サファイアSA100 (⊥c) | 9.3 | <1 |
| アルミナA-445 | ε'=9.8 | ε"=1.96x10-2 |
| イットリアY100A | ε'=11 | ε"=5.5x10-3 |
| サファイアSA100 | ε'=9.3 | ε"<9.3x10-4 |
-------------------------------------------------
誘電体の周波数特性は、誘電分極の種類によって異なります。
共有結合性の誘電体の誘電率は電子分極から生じバンドギャップの大きなものは誘電率のピークはバンド間遷移で起きます。
イオン結晶の場合は、ローレンツ型の分散となり赤外部に共鳴型のピークになります。
液晶などの配向分極の場合は、デバイ型の誘電率分散式で表されます。
デバイの分散式は比誘電率εの角周波数ω依存性として次式で与えられます。
ε(ω)=ε(∞)+Δε/(1+iωτ)
この式では誘電緩和による誘電率虚数部のピークはω=1/τで表されます。
直流における誘電率は
ε(0)=ε(∞)+Δε
で与えられます。
------------------------------------------------------
誘電体については、佐藤勝昭編著「応用物性」(オーム社)第4章(古川猛夫執筆部分)をお読みください。
----------------------------------------------------------------------------------------------------------------------
Date: Thu, 31 Dec 2015 21:40:36 +0900
AA: お忙しい中、早急かつ明快なご回答いただきまして誠にありがとうございます。
なるほど、実数の誘電率は複素誘電率の実数部だったのですね。
自明なことなのか、それを明記した資料がなかなか見つからず、困っていました。
勧めていただいた佐藤先生の書籍を是非読ませていただき、詳しく勉強させていただきます。
本当にありがとうございました。
-----------------------------------------------------------------------------------------------------------------------------------------------
1358. ファラデーの電磁誘導の法則について
Date: Tue, 5 Jan 2016 20:50:04 +0900 Q: 初めまして、突然のメール失礼致します。N*高専5年のI* と申します。
Q: 初めまして、突然のメール失礼致します。N*高専5年のI* と申します。卒業研究で行き詰っていたところ、HPを見てご連絡させていただきました。
電磁気学についての質問です。
現在行っている研究で、準定常状態におけるファラデーの法則について悩んでいます。
質問の内容ですが、
添付した写真のように抵抗を持つ閉回路で積分形のファラデーの法則を適用すると
右辺が0または磁束の時間微分どちらになるのかということです。
準定常状態においてはキルヒホッフの第2法則が成り立つため0となります。
しかし、-gradVが周回積分を行うと0になるのは理解できるのですが、誘導された電場であるベクトルポテンシャルAの時間微分を周回積分 した項が0になるとは思えないのです。
浅学のため的外れなことを考えているかもしれませんが、是非ともご意見を伺わせてください。
よろしくお願い致します。
-----------------------------------------------------------------------------------------------------------------
Date: Tue, 5 Jan 2016 23:12:13 +0900
 A: I君、佐藤勝昭です。
A: I君、佐藤勝昭です。卒業研究の疑問は、本来、指導教員に聞くのが原則です。
理解するには、rotE=∇xEなどの高度な微分演算を学ぶ必要があります。
添付ファイルの式(5)の様に、閉曲線Cに沿ってのEの線積分は ストークスの定理により、∇xEをcが囲む面積積分に等価です。
∇xEは式(4)によれば、磁束密度Bの時間tについての偏微分に等しいので 積分と偏微分の順番を入れ替えると式(5)の4番目の式のように磁束密度の 面積分の時間微分になっている。磁束密度の面積分は磁束Φなので 式(5)の第5式のようになります。磁束の変化がある限り0になることはありません。
--------------------------------------------------------------------------------------------------------------------
Date: Wed, 6 Jan 2016 14:19:00 +0900
AA: お世話になっております。N高専5年Iです。
お忙しい中、早速のご返答ありがとうございました。
---------------------------------------------------------------------------------------------------------------------
1359.液中プラズマについて
Date: Wed, 3 Feb 2016 16:51:13 +0900Q1: HPの方を拝見させて頂いて質問させて頂きました。参考にさせて頂いております。
私はM*大学・理工学部3年のI*と申します。匿名でお願い致します。
授業でプラズマについて勉強しました。なかでも、液中プラズマが注目されていて、 液中プラズマはナノ粒子などの生成に期待されているとのことでした。プラズマに関しては 一生懸命、勉強しまして基本的な知識はあります。
しかし液中プラズマについて調べていく中で、液中プラズマはナノ粒子を合成する際に、 粒子を均一にし、分散性があるということでしたが、その理由が調べても書かれていません。
なぜ、液中プラズマには粒子を均一に分散させる効果があるのでしょうか?
よろしくお願い致します。
---------------------------------------------------------------------------------------------------------------
 Date: Thu, 4 Feb 2016 01:05:39 +0900
Date: Thu, 4 Feb 2016 01:05:39 +0900 A1: I君、佐藤勝昭です。
「液中プラズマ」とは液体中の気泡中に温度数千K のプラズマを発生させる技術です.
数千Kの高温なのでダイヤモンドでも合成できます。気泡は極めて狭い反応場なので、 ナノ粒子を均一に製造するのに向いているのでしょう。
--------------------------------------------------------------------------------------------------------------------
Date: Thu, 4 Feb 2016 11:53:49 +0900
Q2: M大 Iです。迅速な対応ありがとうございます。分散性の高さも同様に反応場が 気泡中の狭い範囲のためだからでしょうか?
よろしくお願い致します。
--------------------------------------------------------------------------------------------------------------------
Date: Thu, 4 Feb 2016 21:20:18 +0900
A2: I君、佐藤勝昭です。
分散性については、東京都立産業技術研究センター研究報告,第10 号,p92 (2015年) が参考になります。
--------------------------------------------------------------------------------------------------------------------
Date: Sat, 6 Feb 2016 13:33:36 +0900
Q3: M大Iです。何度も質問してしまい申し訳ありません。
液中プラズマについて学んで行くうちに疑問に思ったのですが、液中プラズマでナノ粒子を合成する にあたって授業ではいずれも利点しか示されていません。デメリットはないのでしょうか?
よろしくお願い致します
--------------------------------------------------------------------------------------------------------------------
Date: Sun, 7 Feb 2016 22:22:50 +0900
A3: I君、佐藤勝昭です。
J. Plasma Fusion Research Vol.84, No.10 (2008)に次のような記述があります。
「水中でアーク放電を起こすときの電極間距離は約1 mmであるが,電極の間の狭い空間で形成する生成物は陰極上 に堆積した後,放電中に陰極より脱離して水底に沈むことが多い.
また,プラズマから液に向かって移動する炭素蒸気が冷却・固化してできた生成物は,表面が疎水性で粒子径が十分に 小さければ表面張力によって液面に浮遊する.」
と書かれており、実際にナノ粒子生成物を高効率で得るのは工夫が必要だと思います。
また、高圧アーク放電は電源装置が大きく使い勝手が悪いので、最近はマイクロ波液中プラズマを使うことが行われているようです。 例えば、北大先進材料ハイブリッド工学研究室 「マイクロ波液中プラズマ法によるナノ材料の創成」 をお読みください。 いずれにせよ、発展途上の技術なのでスケールアップして生産ラインで使うには、多くの解決すべき課題があるのではないでしょうか。
------------------------------------------------------------------------------------------------------------------------
Date: Fri, 12 Feb 2016 00:07:58 +0900
AA: 佐藤勝昭 様、M大学部Iです。
返信が遅くなり本当に申し訳ありませんでした。
参考文献の方送って頂き大変助かります。
これからもっと勉強していきます。
本当にありがとうございました。
------------------------------------------------------------------------------------------------------------------------
1360.硫酸銅水溶液をビタミンCで還元したときの色
Date: Fri, 12 Feb 2016 01:21:35 +0900Q1: 佐藤勝昭 様、HPを拝見してメールさせて頂きました。
私は個人塾でアルバイトをしています。N*大学2年S*と申します。匿名でお願い致します。
生徒の方から、学校の授業の実験について質問を受けたのですが分かりませんでした。
実験は、硫酸銅五水和物(CuSO4・5H2O)を純水に溶かして硫酸銅水溶液を作製
その後、水酸化ナトリウム水溶液を滴下して水酸化銅(Cu(OH)2)を生成
すると、溶液の色はきれいな青色になります。(銅の錯イオンも関係して?)
ここまでは理解できたのできました(有名な反応ですので)
その後、L-アスコルビン酸(C6H8O6)というビタミンCを入れると緑色になり、さらに入れるとオレンジ色に変化したそうなのです。
その変化の化学式は予想はできるのですが、この色は何が起因しているのか(原子・分子・イオン(錯イオン)など)がわかりません。
お答えができそうであれば、お忙しいところ恐縮ですが、よろしくお願い致します。
-------------------------------------------------------------------------------------------------------------------
Date: Fri, 12 Feb 2016 10:44:50 +0900
A1: S君、佐藤勝昭です。
塾講師なのに熱心に生徒と向き合っておられ感心します。
(以下の説明は高校生には難しいかも知れませんね。)
 Cu2+の水和物(Cu(H2O)6)2+は薄い青色です。この青色の起源は、
Cu2+のもつ3d軌道における配位子場遷移です。Cu2+イオンの3d軌道は、6個のH2O
配位子による配位子場によってエネルギーの低いt2g軌道とエネルギーの高いeg軌道に分裂しています。
Cu2+の水和物(Cu(H2O)6)2+は薄い青色です。この青色の起源は、
Cu2+のもつ3d軌道における配位子場遷移です。Cu2+イオンの3d軌道は、6個のH2O
配位子による配位子場によってエネルギーの低いt2g軌道とエネルギーの高いeg軌道に分裂しています。(この分裂の大きさは配位子の種類によって異なります。共有結合性が強いほど大きくなります。)
添付図1の吸収スペクトルに示す様に、(Cu(H2O)6)^2+は赤の波長域にt2g→egの吸収帯があるのですが、600nm-340nmには吸収が なく、赤の補色であるシアン(青緑)の色が見えます。
 L-アスコルビン酸で還元しますと、第1段階ではCu2+→Cu1+となります。
L-アスコルビン酸で還元しますと、第1段階ではCu2+→Cu1+となります。Cu1+の3d電子は3d10閉殻となりますから、3d電子による配位子場遷移が 減少、L-アスコルビン酸の色(添付図2)の黄色が混じって緑に見えます。
 さらに還元を続けると、Cu1+→Cuとなり、銅のナノ粒子が分散します。
さらに還元を続けると、Cu1+→Cuとなり、銅のナノ粒子が分散します。銅粒子の表面プラズモンの影響で3つめの添付図のように強い橙色に着色します。
図はhttp://pubs.rsc.org/en/content/articlelanding/2011/gc/c0gc00772b#!divAbstract から
---------------------------------------------------------------------------------------------------------------------
Date: Fri, 12 Feb 2016 13:22:29 +0900
Q2: 佐藤勝昭 様
N大学2年 Sです。
詳しい説明のほうありがとうございました。正直に申しますと難しいですね。
(見たこともない用語ばかりで驚きました)
英語の論文まで頂きまして、大変感謝しております。
化学はとても好きなので、これからもっと勉強します。
生徒に少しでもうまく伝えられるように、頂きました資料とともに学習します。
本当にありがとうございました。
----------------------------------------------------------------------------------------------------------------------
Date: Fri, 12 Feb 2016 18:52:05 +0900
A2: S君、佐藤勝昭です。
電気電子工学科2年生では配位子場遷移は学んでいないですね。
私の友人で東大名誉教授の小島憲道先生の基礎現代化学の講義パワポのp25以降が参考になります。
----------------------------------------------------------------------------------------------------------------------
Date: Sat, 13 Feb 2016 02:47:54 +0900
Q3: 佐藤勝昭 様、N大学2年Sです。
ありがとうございます。わざわざ資料まで送って頂き本当に勉強になります。
ここで質問させて頂いてから、自分でもいろいろ調べました。(春休みに入りましたので、、)
すると、一つ論文を見つけまして、読んでおりました。
それは、硫酸銅水溶液にL-アスコルビン酸を入れて水酸化ナトリウム水溶液を入れて プラズマを照射して銅を作製するというものでした。
プラズマについての知識は正直ほとんどありませんが、単純に佐藤様に教えて頂きました、L-アスコルビン酸でオレンジ色の状態 (銅の表面プラズモン)まで還元しているのであれば、そのプラズマというのを照射して銅にするというのが疑問に思いました。
プラズマを照射する前のオレンジの状態で銅なのではないでしょうか?
質問の仕方が下手で、伝わりづらいかもしれませんが、よろしくお願い致します。
--------------------------------------------------------------------------------------------------------------------
Date: Sat, 13 Feb 2016 07:24:52 +0900
A3: 君、佐藤勝昭です。
熱心ですね。
確かにオレンジ色の状態の色をきちんと見たわけではないので、はじめのご質問の最後の状態でCuのナノ粒子まで還元したのか不明ですね。
プラズマ照射と言うのは、おそらく液中プラズマ放電を起こして分散性の高いナノ粒子を作ったのでしょう。
この技術については、なんでもQ&Aの1359番を参照ください。
ナノ粒子の表面プラズモンによるオレンジ色の着色については、金のナノ粒子を分散させたガラスが赤く見えるのと同じで、プラズマを使ったプロセスとは別の話です。
--------------------------------------------------------------------------------------------------------------------
Date: Sat, 13 Feb 2016 10:48:10 +0900 AA: 佐藤勝昭様、Sです。
詳しく対応して頂いて本当に感謝です。プラズマという技術も面白いですね。
生徒に、ちゃんと伝えられるように、もう少し勉強してみます。
本当にありがとうございました。
---------------------------------------------------------------------------------------------------------------------
1361.Er3+イオンの蛍光スペクトル
Date: Thu, 18 Feb 2016 13:17:02 +0900Q: 佐藤勝昭 様
HPを見てこのメールをお送りした次第です。
K高専材料工学科5年のIと申します。
現在、卒業研究において少し行き詰っており、指導教官に質問したところ、佐藤勝昭様のHPで質問してみては?
という助言をいただき、メールさせていただきました。
Er3+イオンのエネルギー準位に関する質問です。
現在卒業研究において、酸化物ナノ粒子にErを添加し、近赤外領域においての蛍光特性の評価を行っています。
Erは光ファイバーや増幅器などに使用されており、980nmの波長で励起され、1550nmの蛍光が起こります。このとき、 励起状態の4I13/2から基底状態の4I15/2への光学遷移によって蛍光が起こります。
ここからが質問となります。
・配位子の影響により4I13/2や、4I15/2の準位が7つ、8つ程細分化されるようなのですが、今のところ細分化された 準位の詳細が書かれている文献が見つかりません。細分化された準位について詳しくご教授いただけないでしょうか。
・また、測定した蛍光スペクトルは1300nmから1600nmの範囲で測定を行ったのですが、①1350nm~1400nm, ②1450nm~1500nm,③1550nm~1600nmにおいて蛍光が起きており、それぞれ①4I9/2→4I15/2,②4I11/2→4I15/2, ③4I13/2→4I15/2の光学遷移によるものだと私は考察しました。③についてはいろいろな文献に書かれていたため、 恐らく当たっていると思うのですが、①と②については詳細な文献がなかったため、断定することができません。
①,②,③それぞれの蛍光はどの軌道の遷移によるものなのでしょうか。
蛍光ピークがどの軌道遷移によるか説明する必要があるので、これらの準位については私にとって大変重要な情報となります。
大変お忙しいところ申し訳ありませんが、学部2年生レベルでも理解できるような説明をお願いしたいです。
それではよろしくお願いいたします。
---------------------------------------------------------------------------------------------------------------
Date: Thu, 18 Feb 2016 15:59:48 +0900
A: I君、佐藤勝昭です。 高専生には程度の高すぎる問題なので、やさしく説明できるか自信がありません。 Er3+は4f電子を11個もっています。4f軌道の軌道角運動量量子数L=3です。ということは、Lz=3, 2, 1, 0, -1, -2, -3なので7個の軌道があります。
この7個の軌道に11個の電子をHund則に従って、スピンの合計がなるべく大きくなるよう詰めていくと7個の上向きスピン電子でLz=3, 2, 1, 0, -1, -2, -3が埋まり、L=0, S=7/2となり、残りの4個の電子は下向きスピンとなってLz=3, 2, 1, 0を占めるので、L=6S=4x(1/2)=2です。上向きと下向きを合計すると、L=6, S=7/2-2=3/2 となります。
L=0,1,2,3,4,5,6に対して、S,P,D,F,G,H,Iで表すことになっているので、軌道角運動量を表す記号はIです。一方、スピンについては、スピン3/2のz成分は3/2, 1/2, -1/2, -3/2の4通りを取れるので、これをIの左肩に書きます。4Iとはそれを表します。一方、添字には基底状態の全角運動量の成分を書くことになっており、4f11の場合は|L+S|=6+3/2=15/2です。それで基底状態は4I15/2と書くのです。
励起状態は|L-S|=9/2, |L-S|+1=11/2,|L+S|+1=13/2を取れるので4I9/2, 4I11/2, 4I13/2の3準位となります。
質問回答1.あなたの①と②, ②と③の平均のエネルギー差はそれぞれ533cm-1, 383cm-1と、ほぼスピン軌道相互作用の大きさなので、アサインはOKでしょう。
結晶場やスピン軌道相互作用を考えなければ4I13/2は13/2,11/2,9/2,7/2,・・,1/2の7つの成分が、4I15/2は15/2,13/2,・・・,1/2の8つの成分が縮退しています。実際には、電子相関、スピン軌道相互作用、結晶場等による分裂が起きます。
固体中の希土類イオンのエネルギー準位の細かい話は、1957年のElliottらの論文 J. P. Elliott, B. R. Judd, W. A. Runciman: Energy Levels in Rare-Earth Ions; Proc. R. Soc. Lond. A 1957 240 509-523 に詳しく書かれています。
Abstractによれば、(a)電子間のクーロン相互作用、(b)電子のスピン軌道相互作用、(c)結晶場 を考慮して論じているようです。(私は読んでおりませんが、高専生にははっきり言って無理です。)
GdOClに添加したEr3+の結晶場を考慮した扱いについては、1997年のHolsoらの論文 J. Holso, E. Sailynoja,R.-J. Lamminmaki, P. Deren, W. Strek, P. Porcher: Crystal field energy level scheme of Er3+ in GdOCl Parametric analysis; J. Chem. Soc., Faraday Trans., 1997, 93, 2241-2246が詳しく扱っています。
Abstractによれば、17個の2S+1 L J 準位; すなわち4f11配置の 182個のクラマース2重項から生じた61 個のスタルク分裂した成分から成り立っているということが書かれています。解析には電子相関を表すラカーのパラメータ (E 0?3 ), ツリーのパラメータ (α, β, γ) 、ジャッドのパラメータ (T k ; k = 2-4, 6-8) およびスピン軌道相互作用定数(ζ 4f)、C4v結晶場を表すBqk(B02, B04, B44, B06, B46)でフィットしたとあります。
質問回答2:微細構造まで説明するのは、高専生レベルでは無理です。、(a)電子間のクーロン相互作用、(b)電子のスピン軌道相互作用、(c)結晶場 などで分裂していると書くべきでしょう。
----------------------------------------------------------------------------------------------------------------------------
Date: Thu, 18 Feb 2016 17:52:31 +0900
AA: 佐藤勝昭 様
早速のご返答、ありがとうございます。
非常にわかりやすいご説明ありがとうございます。
佐藤さんの解説を参考に、卒業研究の考察をさらに深めていこうと思います。
本当にありがとうございました。
-----------------------------------------------------------------------------------------------------------------------------
1362. PVC樹脂の物性
Date: Thu, 10 Mar 2016 08:57:20 +0900Q: 佐藤勝昭様、初めてご連絡をさせていただきます。 Y*社のT*と申します。
佐藤様のHPを拝見して、質問をさせて頂きます。
大変お手数かとは思うのですが、WEBへの掲載の際には、社名、氏名とも匿名にてお願いを致します。
早速ではありますが、樹脂(PVC)の特性について質問をさせていただきます。
『PVCは低温で硬く、もろくなる』というのは一般的な知見だと思うのですが、 日本の1月(冬)の平均気温6.1℃、8月(夏)の平均気温26.7℃(“気象庁 過去の気象データ”より抜粋)。
この20℃程度の温度変化はPVCに対してどれほどの物性変化をもたらすのでしょうか。
樹脂材料をプレス加工しているのですが、冬に樹脂が“欠ける”ということが多々あります。なぜでしょうか。
ご多忙化と存じますが、ご回答のほど宜しくお願い致します。
-----------------------------------------------------------------------------------------------------------------------------
Date: Thu, 10 Mar 2016 10:50:32 +0900
A: T様、佐藤勝昭です。
メールありがとうございます。樹脂は私の専門ではありませんので
Webサイトの情報をもとにでお答えします。
ポリ塩化ビニールのガラス転移温度Tgは83℃です。ガラス転移温度とは液体状態の物質を急冷したとき、安定な結晶状態に転移することなく、 ガラス状態(ランダムな分子配置を持つ状態)に移る温度です。
高分子は一般にTg以上の温度ではゴムのような弾性を示しますが、Tg以下になると、温度が下がるほどもろくなります。
ガラス状態は、非平衡なので何かの外部状況で平衡状態の結晶になり、もろくなります。
(窓ガラスなどが結晶化によって失透する現象がよく知られています。)
PVCにわずかな可塑剤を入れると、Tgを最大-40℃まで下げることができ、室温で、ゴムのような弾性を示します。
可塑剤の量でコントロールできるのではないかと思います。
-----------------------------------------------------------------------------------------------------------------------------
Date: Thu, 10 Mar 2016 12:06:42 +0900
AA: 佐藤勝昭様、Y社のTです。
早々にご回答頂き、ありがとうございました。
樹脂材料において、Tgが重要であり物性変化があることがわかりました。
結晶性か非結晶性の樹脂なのかということも含め、奥が非常に深く“樹脂が欠ける”現象に対して、 紹介していただいたサイトも参考にさせていただき、さらに掘り下げて調べていきたいと思います。
また質問をさせていただく際には、お手数かと思いますが、何卒宜しくお願い致します。
------------------------------------------------------------------------------------------------------------------------------
1363.異種金属の接触電位差
Date: Tue, 12 Apr 2016 14:45:53 +0900Q1: 佐藤勝昭先生 はじめまして。T大学2年のT*と申します。(公開の際は匿名でお願いいたします。)
個人的に太陽電池に興味を持っておりまして、『太陽電池のキホン』や『高校数学でわかる半導体の原理』などでまずは基本的なことから 勉強をしております。しかし、半導体や金属の接合について根本的な理解が出来ていない点があると感じており、 思い切ってこちらにて質問させていただくことにしました。初歩的な質問で恐縮ですが、お教えいただけますでしょうか。
① 異種金属同士の接合では、仕事関数の差分の接触電位差が生じるということですが、これは半導体同士の接合で見られる様な電位の曲がりは起こらず、 界面においてステップ状に電位が変化するという理解で正しいでしょうか?
その場合、接合界面にプラスとマイナスの電荷が貯まることで一種のコンデンサーの様な状態になっているのかと想像しており、例えばAlとAuの接合の場合、 どれくらいの電子が動くか計算してみたいと思いました。しかし、コンデンサーとして捉えた場合の電極間の距離dがどうもうまく定義できず、 行き詰まってしまいました。異種金属接合界面における電子移動の量などを定量的に算出できる方法などあればお教えいただけたらと思います。
また、こうして接合した異種金属の場合、接合したままの状態でAl側とAu側での仕事関数をそれぞれ測定したとすると、その値は同じになるのでしょうか、 それとも異なるのでししょうか?もともとのAlとAuの仕事関数がそれぞれ得られるのだとしたら、接触電位差で生じた電位差はどこに行ってしまうのでしょうか? Alに対してAu側の電位が高い状態(電位がマイナス)になっているのだとしたら、Alに接合したAuから電子を引き出す場合と、独立したAuから電子を引き出す場合と では必要なエネルギーが異なる様に感じてしまいます。真空準位がシフトするという説明がなされる場合もありますが、真空準位とは無限遠の真空状態を仮定した 時の電位だと理解しており、その値が変動してしまうという解釈にも違和感があります。
② 「なんでもQ&A」No.728の図bにおいて、 n型半導体側にφm-φsの電位差が生じていますが、金属側に溜まった電子は、質問①の金属同士の接合で見られるようなステップ状の電位変化を生まないの でしょうか?半導体側のプラス電荷と同じ量だけの電子が、接合界面の金属側に溜まっているように思い、半導体側と金属側でそれぞれ(φm-φs)/2ずつの 電位差を生み出し、半導体側はバンドが曲がるけれど金属側では電子が自由に動けるためにステップ状の電位変化になるのではないかと思ってしまいます (もちろん、半導体側だけに電位をかけることは難しいので、この場合も障壁を越えるためにはφm-φsの電圧が必要であることに変わりはないのですが)。 全ての電位差が半導体側だけで作られるというのはどういった原理によるものなのでしょうか?
また、同図cにおいて、半導体側のバンドが曲がる理由がわかりません。 参考書などで「空乏層ができるためバンドが曲がる」といった説明をよく目にするのですが、n型半導体と金属のオーミック接合の場合、n型半導体に電子が 注入する形になると思います。もともと電子が多い状態にさらに電子が増えるだけなので、空乏層はできないように思うのですが、間違いでしょうか? 「空乏層ができる」=「バンドが曲がる」という理解が違うのか、あるいはこの場合でも空乏層はできているのでしょうか?同様に、真性半導体と金属の 接合でも、こういったバンドの曲がりは生じるのでしょうか?
③ 「なんでもQ&A」No.366で 縮退半導体のことを知りました。金属に似た性質も示すということですが、縮退半導体と金属を接合した場合は、①の金属同士の接合のように接触電位差が 生じて界面でステップ状の電位変化が生じるのでしょうか?それとも、②の縮退していない半導体と同様に、バンドの曲がりが生じるものなのでしょうか?
縮退半導体を用いるとオーミック接合を作れる原理が、「バンドは曲がるけれど、空乏層の幅が狭くなってトンネル電流が流れる」ということなのか、 それとも「バンドは曲がらずに金属同士の接合と同様に扱える」ということなのか、どちらでしょうか?あるいはこの2つは連続した現象で、金属同士 の接合の場合にも、細かく厳密に見ていけば半導体の時のようなバンドの曲がりが、極僅かな幅で急激にあるものなのでしょうか?
初歩的な質問で恐縮ですがお教えいただけますでしょうか。よろしくお願いいたします。
----------------------------------------------------------------------------------------------------------------------------------------
Date: Tue, 12 Apr 2016 23:18:23 +0900
A1: T君、佐藤勝昭です。
 確かに、金属/絶縁体/半導体(MIS)構造や、金属/半導体ショットキー接合は
固体物理の教科書に出ていますが、異種金属の接合については載っていませんね。
金属どうしの接合については立教大サイトが参考になります。
確かに、金属/絶縁体/半導体(MIS)構造や、金属/半導体ショットキー接合は
固体物理の教科書に出ていますが、異種金属の接合については載っていませんね。
金属どうしの接合については立教大サイトが参考になります。添付図に従って説明しますと
(a)仕事関数が異なる2つの金属A,Bがあったとします。
(b)電子がBからAに移動してフェルミ準位EFが同じになるまで電子が移動します。
(c)電子の移動に伴って真空準位が下がります。これはEFから見る真空準位が、 電子の移動する前と同じでなくてはならないためです。
この結果真空準位に仕事関数差の電位差が生じます。これが接触電位差です。 (d)金属の表面には、電子が出て行ったB側にプラスの表面電荷が、電子を受け入れたA側にマイナスの表面電荷が生じます。
光電子放出実験によって電子が飛び出す閾値を測ると、接合前の仕事関数が得られるはずです。
一方、金属と半導体のショットキー接合を考えますと、半導体側の空間電荷の分布を考慮したポワソンの方程式を解くと、距離に対し2次関数で変化します。
佐藤勝昭編著「応用物性」(オーム社)p88-89のショットキー接合の記述(添付)を参考にして下さい。
学部3年になってから学ぶと思いますが、量子論に基づく固体物理学、特に、フェルミ準位について、よく学習しておいてくださいね。
各質問にお答えします。
(1) 金属内では、電位の曲がりは起きません。電磁気学で学んだように、理想的には導体内は電位が一定です。
接合界面における電荷の動きですが、フェルミ準位をそろえるためにどれだけ電荷移動が起きるかを計算する必要があります。
きちんとやろうとすると、バンド計算をしてフェルミ面付近の電子の状態密度を見積もる必要があるでしょう。
(2) 金属・金属接合面で電子のエネルギーはステップ状には変化しません。
真空準位の電位が変化するのです。電磁気学では、金属内の電位は一定ですが、n型半導体側は、界面付近の電子が金属に流れ込んだため、 プラスの空間電荷の分布ができたので、ポワソン方程式に従って2次関数的な電位変化が生じます。
金属側に入った電子は通常は多数の電子の海に少しだけ入ったので、電位変化は無視できますし、界面には結合の切れたことによる トラップ準位があるので、そこに捕まっているはずです。
 (3) 縮退半導体は、フェルミ準位が伝導帯に入っているので、金属的な電気伝導を示しますが、キャリア密度は金属に比べ圧倒的に
少ないので、電子が金属に流れ込んでフェルミ準位を一致させた結果、界面には正の空間電荷ができ、非常に薄いポテンシャル障壁
が生じます。しかし、大変薄いので、トンネル的に電流は流れ、オーム性接触になると考えられます。
(3) 縮退半導体は、フェルミ準位が伝導帯に入っているので、金属的な電気伝導を示しますが、キャリア密度は金属に比べ圧倒的に
少ないので、電子が金属に流れ込んでフェルミ準位を一致させた結果、界面には正の空間電荷ができ、非常に薄いポテンシャル障壁
が生じます。しかし、大変薄いので、トンネル的に電流は流れ、オーム性接触になると考えられます。産総研の半導体解説サイト を参考にして下さい。
(3度にわたってメールで回答したものを、ここではまとめて示してあります。)
-----------------------------------------------------------------------------
Date: Fri, 15 Apr 2016 19:08:31 +0900
Q2: 何度もご返信いただき、ありがとうございます。電車や会議の合間を利用してこんなに早くお返事いただけるとは思っていなかったので、ただただ感謝でいっぱいです。
始めはあまり理解が進まず、どういう風に質問をし直したら良いものかとあれこれ考えていたのですが、 何度も丁寧なご回答をいただけたことで、接合界面を介して電荷が移動して真空準位が変化する様子を イメージすることができるようになりました。「応用物性」も図書館で読むことができ、 真空準位の曲がりが空間電荷の分布によってポワソン方程式を解くことで得られる 2次関数なのだということがよく分かりました。
この考え方でいくと、異種金属の接合においても、極端にキャリア密度が低い金属を用いたとすると、 フェルミ準位をそろえるために電荷が移動することで空間電荷の分布が生まれ、 ポアソン方程式を解けば半導体の場合と同じような2次関数的な真空準位の曲がりが得られると思うのですが、 正しい理解でしょうか?
(そこまでキャリア密度の低い金属、というものが存在するのかはわからないのですが、理論上の話です。)
重ねての質問になってしまって恐縮ですが、お教えいただけましたら幸いです。
-------------------------------------------------------------------------------
Date: Fri, 15 Apr 2016 20:36:12 +0900
A2: T君、佐藤勝昭です。
「極端にキャリア密度が低い金属」ですが、縮退半導体がそのケースです。
金属と呼ばれるものでは、キャリア濃度は1022/cm3程度あるのに対し 縮退半導体のキャリア濃度は1018/cm3~1020/cm3程度です。
酸化物の中には、絶縁体だけどMott-Transitionを起こして金属的伝導を示すものがあります。
例えば、Li_x Zn_(1-x) V_2 O_4などがその例です。このような「金属」では、ご指摘のような ことがおきますが、Au, Ag, Alなどの本当の金属では、桁違いにキャリア密度の低いものは ありません。半金属Biなどはこれより小さいです。
--------------------------------------------------------------------------------------
Date: Mon, 18 Apr 2016 14:24:21 +0900
AA: 佐藤先生
ご返信ありがとうございます。おかげさまで混乱していた頭がすっきりと整理できました。
これで、もう少し難しい参考書なども読んでいけそうです。引き続き勉強させていただきます。
丁寧にご回答くださり感謝いたします。ありがとうございます。
--------------------------------------------------------------------------------------
1364.希土類イオンの蛍光スペクトルについて
Date: Mon, 02 May 2016 15:30:43 +0900Q1: 佐藤勝昭先生へ
私はG*大学大学院機能材料工学専攻M2のK*と申します。ホームページを拝見し質問をさせていただきました。(匿名でお願いします。)
現在、磁性と蛍光について研究しておりますが理解できない点が多く、思い切って質問させていただきました。初歩的な質問ばかりですかお願い致します。
- 希土類の蛍光についてですが遷移の仕方として電気双極子と磁気双極子遷移があるということが分かりました。その名前の由来などなぜそのような名前なのですか?
- また、それが遷移確率を級数展開し、その一項目と二項目ということも分かったのですがスピン軌道相互作用を考えずLS結合だけの場合、軌道角運動量子数L、
スピン角運動量量子数S及び全角運動量量子数Jがどのように変化した場合でしょうか?
例としてイッテルビウムイオン(Yb3+)は2F7/2から2Fsub>5/2への遷移ということがディーケダイアグラムからわかりましたがこれは電気双極子遷移ですか?
- イッテルビウムイオン(Yb3+)についてです。ディーケダイアグラムでは2F7/2と2Fsub>5/2の二つの準位しか記述されていません。
電子配置では2D5/2の準位もあると思うのですがなぜでしょうか。遷移しないから書いてないのか、そもそもそんな準位がないのでしょうか?
- 磁場中の蛍光についてです。磁場を印加した状態で蛍光を測定すると準位がゼーマン分裂を起こすと考えているのですが実際に蛍光スペクトルは分裂するのでしょうか。
または、結晶場とスピン軌道相互作用によって既に準位が開裂しているため蛍光スペクトルは分裂などせずに位置が変化するなどしか起こらないのでしょうか?
- 一成分で強磁性体であり蛍光を示す物質は多々あるのでしょうか。私自身論文を調べましたが磁気特性、蛍光特性及びその相関を調べたものは見つかりませんでした。もしご存知なら教えて頂くことはできないでしょうか?
Date: Mon, 2 May 2016 23:40:51 +0900
A1: K君、佐藤勝昭です。 質問が膨大で、光物性の教科書を数冊分の内容です。短い回答でどの程度わかって頂けるか自信がありませんが、手短に説明します。 あなたは機能材料工学専攻なので、量子力学の基礎知識があるものとして説明します。 参考になるサイト:
新潟大学佐藤研究室のHP
名古屋大学の授業サイト
- 電気双極子遷移と磁気双極子遷移
光学遷移とは電磁波と物質の相互作用によって基底状態に励起状態が部分的に混じることと解釈できます。
電磁波は電界と磁界が互いに直交して振動している伝搬します。
電磁波の電界成分Eと相互作用するのは、電気双極子モーメントPです。相互作用のエネルギーは、P・Eであらわされます。
この摂動を受けて基底状態に励起状態が部分的に混じると電気双極子遷移が起きると解釈されます。
i番目の電子の位置ベクトルをriとすると、
P=-eΣri で表されます。
一方、電磁波の磁界成分Hと相互作用するのは、磁気双極子モーメントMです。相互作用のエネルギーは、M・Hで表されます。
この摂動を受けて基底状態に励起状態が部分的に混じると磁気双極子遷移が起きると解釈されます。
磁気双極子モーメントMは軌道角運動量の量子liとスピン量子siを使って
M=βΣ(li+2si) で表されます。
電気双極子遷移は強い遷移です。磁気双極子遷移の振動子強度は電気双極子遷移のそれの1万分の1位しかありません。
従って、電気双極子遷移禁止の場合にしか観測されません。
- 電気双極子遷移と磁気双極子遷移の量子条件
希土類イオンの4f電子間の遷移はパリティが同じなので基本的には電気双極子遷移が禁止されています。
Yb3+は4f13なので、f軌道に1個ホールがある状態です。Hund則に従うと基底状態は、L=3、S=1/2となります。more than halfなのでJ=L+S=7/2です。
軌道はラッセル-サンダース項ではL=0,1,2に対応してS, P, D, Fと書きます。
左肩にはスピン多重度 2S+1=2x(1/2)+1=2 を 書きます。2Fです。J=L+S=7/2ですが、Jz=7/2, 5/2 これは、Lz=3, Sz=±1/2に対応します。
これがDieke Diagramの2F7/2と2F5/2に対応します。
ΔJz=1なので、磁気双極子遷移ではないかと思われますが、磁気双極子遷移は弱いのでほとんど光らないはずです。
一般に希土類イオンが、結晶内におかれたときに何らかの理由でパリティ禁止が解ければ電気双極子許容になります。
私どもの研究ではCuAlS2:Yb3+で2F5/2→2F7/2の強い赤外発光スペクトルを観測しています。CuAlS2は中心対称性がないので、電気双極子遷移が見られたと考えています。
T.Nishi, Y.Kimura,K.Shimizu, K.Sato: Infrared Photoluminescence Studies of Rare Earth Doped CuAlS2 Single Crystals; Inst. Phys. Conf. Ser. No. 152, pp. 369-372 (1998)
- Yb3+の励起準位2D5/2が書かれていない理由
2F5/2→2D5/2は40,000cm-1位の紫外域に来ることが下記の書物にあります。
D.S.McClure: Electronic Spectra of Molecules and Ions in Crystals Part II Spectra of Ions in Crystals; Solid State Physics Vol.9 (eds. F.Seitz , D.Turnbull), p457 (1959)
------------------------------------------------------
Ce3+(4f1)は電子1個なので、ホール1個のYb3+と同じようなスペクトルになると思いますが、Ce3+では4f7→4f6 5d1 というf→d許容遷移が可視に現れ2F7/2→2D5/2はf→d遷移に隠れて観測されません。
- 実際に希土類イオンの蛍光スペクトルはゼーマン分裂するか?
希土類ドープ半導体において、ESRが見られます。磁界によってゼーマン分裂した基底状態間の磁気双極性遷移がESRです。たとえば、私どもの論文を見てください。
I.Aksenov,Y.Kudo, K.Sato: Electron Spin Resonance of Tb3+ ion in CuAlS2; Jpn. J. Appl. Phys. 31 L1009 (1992)
またEuドープCaSにおいて、蛍光の磁気円二色性(MCE)が見られます。
これはゼーマン分裂した4f7→4f6 5d1遷移のゼロフォノン線のゼーマン分裂を見ていると考えています。私達の論文です。
S.Kijima, K.Sato, T. Koda: Spectra of magnetic circular dichroism of absorption and luminescence of Eu-doped CaS single crystals; J. Luminesc. 55 187 (1993)
- 強磁性体であり蛍光を示す物質
強磁性半導体EuSは、赤色の蛍光を示します。キュリー温度以下で波長が磁気シフトします。
たとえば
G.Busch,P.Streit,P.Wachter:Effect of magnetic ordering on the photoluminescence of EuS and EuTe; Solid State Commun. 8 1759-1763 (1970)
をお読みください。
Date: Fri, 06 May 2016 19:16:53 +0900
Q2: 佐藤勝昭先生へ
ゴールデンウィーク中にも関わらずメールのご回答ありがとうございました。
現在確認することができる論文と先生の説明について考えましたがまだ分からな いことが多いため、もう一度勉強し直してみたいと思います。
それでもまだ解決できないことがあれば再度先生にご質問したいと考えています。
その際にはお手数かと思いますがよろしくお願いします。
長期休暇の中色々な事を教えて頂きありがとうございました。
------------------------------------------------------------------------------------------------------------------
Date: Fri, 6 May 2016 22:12:52 +0900
A2: 君、佐藤勝昭です。
ジャッド=オーフェルト理論(英: Judd-Ofelt theory)をご存じですか?
本来は禁制遷移である4f軌道間の電気双極子遷移が、配位子場の対称性が 崩れることで一部だけ許容化されることを定量的に説明した理論です。
Judd, B.R., Optical absorption intensities of rare-earth ions, Phys. Rev. 127, 750-761 (1962).
Ofelt, G.S., Intensities of crystal spectra of rare-earth ions, J. Chem. Phys. 37, 511-520 (1962).
しかし、YAG:Yb3+の発光に関してはJudd Ofeltでは十分説明できないとされ、理論的に検討されています。
G. G. Demirkhanyan: Intensities of inter-Stark transitions in YAG-Yb3+ crystals;
Laser Physics, Volume 16, Issue 7, pp 1054-1057 (2006)
----------------------------------------------------------------------------------------------------------------
Date: Mon, 09 May 2016 13:36:36 +0900
Q3: 佐藤勝昭先生へ
ジャッドオーフェルト理論は名前しか聞いたことがなかったため先生から教えていただいた論文で勉強したいと思います。
前回のメールの内容に戻ってしまうのですがLS項は電子の入り方という認識なのですが間違っているのでしょうか?
先生から頂いた論文(希土類のスペクトルと磁性)から電子が二つの場合配置方法が91個のパターンがあると書かれています が、現れる多重項としては7パターンです。
縮退している事も書かれていますがL=4,S=0とL=4,S=1は縮退しているということでよろしいのでしょうか?
またなぜ縮退するのでしょうか?同じ軌道角運動量でもどの軌道か及びでの向きのスピンかで全ての準位は開裂すると私自身は考えています。
お手数かと思われますがよろしくお願いします。
----------------------------------------------------------------------------------------------------------------
Date: Thu, 12 May 2016 01:02:11 +0900
A3: K君、佐藤勝昭です。
 添付図はf電子が2個ある場合のL,Sの様子を示しています。
添付図はf電子が2個ある場合のL,Sの様子を示しています。基底状態は(1)の3Hですが、L=5 の場合の多重度は
Lz=5,4,3,2,1,0,-1,-2,-3,-4,-5の11とおりが同じエネルギーを持ちます。
また、S=1のスピン多重度は
Sz=1,0,-1の3通りが縮退しています。従って、軌道の11通りと スピンの3通りで11x3=33通りが同じエネルギーを持ちます。
このあたりは、原子中の電子の量子状態の基礎です。
なんでもQ&Aに頼るのではなく、教科書を1から読み直してください。
-----------------------------------------------------------------------------------------------------------------
Date: Mon, 16 May 2016 10:58:02 +0900
AA: 佐藤勝昭先生へ
初歩的なことばかり質問してしまい申し訳ありませんでした。
もう一度最初から勉強し直そうと思います。
また先生から教えていただいた論文についても理解を深めたいと考えています。
今回の数多くの質問に回答して頂いた事、さらに論文まで教えていただいた事にとても感謝しています。
また先生にお会いする機会がありましたら再度お礼を申し上げたいですが、今回はこのメールでお礼を申し上げます。誠に有難うございました。
---------------------------------------------------------------------------------------------------------------
1365.金属の色の物理的起源について
Date: Tue, 10 May 2016 11:47:59 +0900Q: 佐藤先生 恐れ入れます。初めまして。
S社Kと申します。
金属の色の物理的起源を読みました。
非常に役に立ちまして有り難うございます。
内容中、光子エネルギーを用いた方が、電子の集団運動や電子遷移を表すのに適しているからであるという内容があります。
この意味の説明をお願い致します。
背景としては、
銀蒸着し、反射率を測定する際、蒸着フィルムを用いてエージングすることによって、b値が下がり、反射率が若干高くなる現象が発生しております。
ご検討をお願い致します。
---------------------------------------------------------------------------------------------------------------
Date: Tue, 10 May 2016 21:22:35 +0900
A: K様、佐藤勝昭です。
「光子エネルギーを用いた方が、電子の集団運動や電子遷移を表すのに適している」 の意味ですが、光の吸収は、物質中の電子が基底状態から励起状態に遷移することで 表され、両状態のエネルギー差に相当する光子エネルギーをもつ光を吸収するからです。
波長λ(nm)とエネルギーE(eV)の関係はE=hc/λ=1239.8/λで表されます。波長を使うと逆数なので面倒くさいでしょう?
また、電子の集団運動を特徴付けるのはプラズマ周波数ν_pですが、プラズモンのエネルギーE_pとプラズマ周波数ν_pとの間にはE_p=hν_pの関係があります。
そういうわけで、波長より、エネルギーを使う方が、物理現象をよく記述できるのです。
ご質問「銀蒸着し、反射率を測定する際、エージングすることによってb値が下がり、反射率が若干高くなる現象」については、詳細が書かれてないのでよくわかりませんが、 一般に、蒸着したばかりの銀薄膜は、島状に銀粒子が付着しているため、b値(光散乱)が大きいですが、数百度、数日の熱処理で、島と島が凝集して、平坦になり、散乱が減 り反射率が上がるのだと存じます。
--------------------------------------------------------------------------------------------------------------
Date: Wed, 11 May 2016 10:32:42 +0900
AA: 佐藤様
御連絡を頂いて有り難うございます。
---------------------------------------------------------------------------------------------------------------
1366.ナノ粒子の液相分離
Date: Thu, 26 May 2016 17:29:22 +0900Q: HPの方を拝見して質問させて頂きました。参考にさせて頂いております。
私はM*大学・理工学部・電気電子工学科に所属している4年のI*と申します。匿名でお願い致します。
以前、3年生の時に液中プラズマについて質問させて頂きました。その節はありがとうございました。再度、質問したいことがありますのでお願い致します。
実験で、液相還元法で作製したナノ粒子の溶液(均一に分散されています)の回収方法として吸引ろ過を採用しているのですが、 濾過した後メンブレンフィルターには膜状のもの(SEMで見ても膜状になっていてナノ微粒子は確認できません)になってしまいます。
論文などのきれいな粉末は得られず、濾過方法までは記載されていません。やはり洗浄(エタノールなど)などの作業をしていないことが原因なのでしょうか?
分かりづらくて申し訳ありませんが、よろしくお願い致します。
----------------------------------------------------------------------------------------------------------------
Date: Sun, 29 May 2016 00:12:48 +0900
A: I君、佐藤勝昭です。
同じ質問をGoo Q&Aにも出していますね。ベストアンサーはまだですか?
4年生なら卒論研究室の指導教員がいるはずです。ネットで調べる前に、指導教員に聞くべきでしょう?
私は、化学工学は専門ではありませんが、ナノ粒子の吸引濾過による完全分離は簡単ではないと思います。
論文を探してみましょうね。
ナノ粒子の液相分離法のうち等密度遠心法が優れているようです。
-----------------------------------------------------------------------------------------------------------------
Date: Tue, 31 May 2016 13:37:50 +0900
AA: 佐藤勝昭 様、Iです。
おっしゃる通りです。本来はネットではなく、担当教員に聞くべきでした。考えを改め直します。
資料を送って頂きありがとうございました。是非参考にさせて頂きます。
------------------------------------------------------------------------------------------------------------------
1367.金属薄膜の表面プラズモンについて
Date: Tue, 31 May 2016 01:37:41 +0900Q: 佐藤勝昭先生
HPを拝見させていただきました。K*大学修士1年のT*と申します。Webへ掲載する名前は匿名でお願いいたします。
------------------------------------------------------------------------
以下、基板上に非常に薄い薄膜があることを想定させていただきます。
膜厚10 nm程度の薄膜に表面プラズモンが励起する場合、膜厚が非常に薄いために薄膜の上表面と下表面の両者に表面プラズモンが 励起して相互作用し合い、高周波数と低周波数の2つの励起モードが生じるという論文をいくつか見つけました。
こういった論文は電子エネルギー損失分光法(EELS)に関する論文で多く見受けられ、薄膜の横から100 keV程度の電子を入射した時 に生じる現象について議論しています。
------------------------------------------------------------------------
参考
E. A. Stern et al., Surface plasma oscillations of a degenerated electron gas, Physical review 20, 130 (1960).
また、その励起される表面プラズモンの波長などについては触れられていません。
そこで質問なのですが、
誘電体基板上の金属薄膜 (膜厚10 nm程度) へ強い光を入射させた場合、薄膜上表面と基板との境界面の両者において表面プラズモンが励起し、2つの励起モードは生じ得るでしょうか。
また生じる場合は、2つの表面プラズモンはどれくらいの波長を持っているのでしょうか。求め方等があればご教示頂ければと思います。
以上、お手数おかけいたしますが、ご返答頂けますと幸いです。
---------------------------------------------------------------------------------------------------------------------------------------------------
Date: Wed, 1 Jun 2016 00:13:40 +0900
A: T君、佐藤勝昭です。
SiO/Si界面のプラズモンは、価電子プラズモンで、金属薄膜に見られる自由電子プラズモンとは異なり 6.5eV(波長190.7nm), 9eV(137.8nm)の紫外線領域に現れます。プラズモンは縦波なので、電子線では吸収 が見えますが、光では明確には見えません。
ご質問の金属薄膜/誘電体においても価電子プラズモンは見られますが、あなたの考えているのは近赤外 ~可視域に現れる自由電子プラズモンではないのですか?
表面プラズモンの干渉は、近接場を使うと見ることができます。例えば、
Li Jiang-Yan et al., Chin. Phys. B Vol. 22, No. 11 (2013) 117302 を読んで下さい。
-----------------------------------------------------------------------------------------------------------------------------------------------------
Date: Sat, 11 Jun 2016 01:27:49 +0900
AA: 佐藤勝昭先生
お返事遅くなり申し訳ありません。
早急なお返事をありがとうございました。是非、参考にさせていただきます。
誠にありがとうございました。
----------------------------------------------------------------------------------------------------------------------------------------------------
1368.錫メッキ線とアルミカシメを画像処理で区別したい
Date: Mon, 1 Aug 2016 03:26:55 +0000Q: 東京農工大学 佐藤勝昭様、A社Hと申します。
始めて、メールをさせて頂きます。
先生の研究室に光を用いた金属の反射の資料が有る事をインターネットを介して知った事でメールしています。 現在、弊社ではコネクター端子のカシメの部分を画像処理を用いて出荷検査を行っております。
私共の悩みは、線材が銅からアルミに変わったことで端子の色(錫メッキ色)とアルミ電線の色の見分けが付かず 画像処理による出荷検査に手間取ってます。
そこで、検査する光の波長を変えることによって、うまく画像を読み取る事が出来ないかと思い、何か良いアドバイス を頂けないかと思い、不躾ですがメールをさせて頂きました。
------------------------------------------------------------------------------------------------------------------------------------------------------
Date: Wed, 3 Aug 2016 23:24:21 +0900
 A: H様、佐藤勝昭です。
A: H様、佐藤勝昭です。高松に出張中だったため、お返事が遅くなり申しわけありません。
スズはありふれた金属ですが、私の手持ち反射スペクトルは半導体の灰色スズしかありません。
メッキで堆積した銀白色のスズは白色スズだと思われますので、下記論文を、長岡技科大の石橋先生にお願いして取り寄せてもらいました。
G Jezequel, J C Lemonnier and J Thomas, Optical properties of white tin films between 2 and 15 eV, Journal of Physics F: Metal Physics, Volume 7, Number 12
添付の図は左がアルミ、右が白色スズです。横軸EはeV単位で描かれています。光子エネルギーE(eV)を波長λ(nm)に変換するには、λ=1239.8/Eの式を使います。
図のように、AlとSnの反射スペクトルは非常に似ていますが、Alの方が全体に反射率が高くなっています。しかし、Al表面は酸化膜ができているので、反射率 は図のスペクトルより低く、スズとあまり変わらないと思います。
従って、スペクトルを詳細に測定しない限り、AlとSnを完全に区別することは不可能です。
あまりお役に立てなくて申しわけありません。
---------------------------------------------------------------------------------------------
AA: お忙しい中、ご連絡有難う御座いました。
実は、本件に付いては複数のテ゛ハ゛イスメーカーや画像検査メーカーに問い合わせを行っていましたが、何処からも 出来ないとの回答を受け大変困っていた所です。ご意見を頂いた内容で検討をして見ます。
--------------------------------------------------------------------------------------------
1369.アルマイト処理したアルミ表面の輻射率について
Date: Sat, 20 Aug 2016 23:05:02 +0900Q: 初めまして。N社Tと申します。
突然のご連絡にて大変恐縮ですが、ホームページを拝見し質問させて頂きたく存じます。
なお手数ですが、Webに掲載の際は、社名、氏名とも匿名にてよろしく御願いいたします。
========================
教えていただきたいこと
Q1:筐体の放熱設計を行うにあたり、
アルマイト処理後の表面に、油などの汚れが付着することによって
輻射率への影響があるのでしょうか?
アルマイトによる輻射率のアップは、表面粗さのために
反射率が低下することと、表面積が拡大するために起こると考えおります。
その際、細孔も輻射率の寄与につながっているのではないかと考えているため、
(封孔処理をしても、厳密には穴は塞がらないため、輻射率の低下は起きない?)
表面に油などの汚れが、細孔のなかまで付着してしまうことで、
表面のよごれを拭き取っても、輻射率がさがってしまうことがあるのでしょうか?
=========================
私の輻射率に関する理解が間違って居る部分があれば、ご指摘いただければと思います。
お忙しいところお手数おかけいたしますが、ご回答いただければ幸いです。
-------------------------------------------------------------------------------------------
Date: Sun, 21 Aug 2016 17:20:16 +0900
A1: T様、佐藤勝昭です。
はじめに輻射率emissivityについて考えましょう。T>0Kにおかれたすべての物質は熱輻射をします。
熱輻射の大きさは、それぞれの温度、輻射光線の波長において、輻射率に依存します。
輻射率は、物体の表面から輻射されるエネルギーと、同じ温度・波長・観測条件における黒体輻射の エネルギーとの比で表され、0(完全反射)と1(完全輻射)との間をとります。
輻射率は、物質に依存するだけでなく表面の性質に依存します。
よく研磨したアルミニウムの輻射率は0.02(25℃), 0.03(100℃)と非常に小さい値です。アルミニウム を陽極酸化(アルマイト処理)すると、表面にほぼ垂直に無数の細孔があくとともに、その細孔壁は、 Al2O3膜に覆われています。Al2O3の輻射率は0.4程度なので、確かに多少の輻射率の向上があるでしょう が、輻射率の一覧表に載っているアルマイト処理した値の0.77にはなりません。
(アルミナ粉末の輻射率は0.8-0.9と大きいですが、これは粒界面での多重反射によると考えられ、 今回の場合には当てはまらないでしょう)
おそらく陽極酸化したアルミに入射した光は細孔壁で何度も反射を受け強い吸収を受けるのではない でしょうか。理想的にはすべての光が吸収される黒体になりますが、通常のアルマイトではそこまで ではなく77%位吸収されます。逆に、ある温度に置かれたアルマイト処理したアルミからは、黒体の77% くらい光を輻射すると考えられます。
封孔処理では、水和アルミナAlO(OH)で細孔を埋めます。正確には細孔壁の酸化皮膜を覆います。
アルミナと水和アルミナは屈折率が近いので輻射率にはあまり影響がないと考えられます。
油の屈折率は1.45~1.55程度で、酸化アルミニウムの1.76に比べ小さいので界面での屈折が起きて 細孔からの輻射光線に多少の影響があるかも知れません。薄ければ問題ないと思いますが、油膜が 厚いと輻射率が低下すると考えられます。
----------------------------------------------------------------------------------------
Date: Sun, 21 Aug 2016 23:43:53 +0900
Q2: この度はご丁寧なご回答を頂き、ありがとうございます。
やはり細孔による形状的な影響で、輻射率が上がっているということなのですね。
ただお答えをうけて、もう一点疑問が生じましたので質問させてください。
===============================
油膜の厚みによって、輻射率に影響があるとのことですが、
あくまで、表面の汚れは拭き取った状態(細孔のみがつまった状態)では、
細孔はnmレベルの直径ですので輻射にはほぼ影響がないと
いうことで考えてよろしいでしょうか?
===============================
よろしく御願いいたします。
-----------------------------------------------------------------------------------------
Date: Mon, 22 Aug 2016 06:47:22 +0900
A2: 別の見方をすると、細孔を含めたアルマイト表面の見かけの平均屈折率が空気の屈折率に近いほど、 輻射率は高いと考えてよいと思います。
細孔の空間が油で埋まれば、見かけの屈折率が高くなるので、輻射率は低下するのではないでしょうか?
----------------------------------------------------------------------------------------
Date: Tue, 23 Aug 2016 22:16:18 +0900
AA: 度々のご返答ありがとうございます。
大変参考になりました。
お忙しいところ誠に有難うございました。
-----------------------------------------------------------------------------------------
1370.磁性体のヒステリシス損失の熱化メカニズム
Date: Tue, 1 Nov 2016 22:02:26 +0900Q1: 東京農工大学 佐藤勝昭先生
突然のメールで失礼いたします。N*高専・専攻科2年のK*と申します。(匿名でお願いします)
佐藤先生のHPをいつも興味深く拝見しています。
磁性体のヒステリシス損失に関して分からない点があり、ご連絡いたしました。
基本的な内容かも知れませんが、ご教示いただけると幸いです。
現在、変圧器用コアのヒステリシス損失について調べており、調査した多くの文献には 「ヒステリシス曲線のループ面積が1周期の損失となる」と書かれているのみで、どのような 仕組みで熱が発生するのか、見いだすことができませんでした。
そもそも、ヒステリシス曲線のループ面積には、ヒステリシス損だけでなく渦電流損も含まれ、 周波数とともに影響が大きくなってくるものと認識しております。
熱の発生原理として、バルクハウゼン効果に伴う急激な磁壁移動で発生する渦電流損、 電子スピンが向きを変える際に発生する摩擦熱?など、様々考えていますが、実際に静磁 エネルギーから熱エネルギーへの変換プロセスがどうなっているのか、よくわかりません。
可能ならば具体的なイメージとして現象をとらえたいと考えていますが、量子論の十分な 知識がないとなかなか理解できない領域なのでしょうか。
お忙しいところ大変恐縮ですが、何卒、助言をくださいますよう、よろしくお願いいたします。
--------------------------------------------------------------------------------------
Date: Wed, 2 Nov 2016 00:07:24 +0900
A1: K君、佐藤勝昭です。
するどい質問ありがとう。
永久磁石のヒステリシス曲線のループ面積は磁石が蓄えている静的な磁気エネルギーです。
一方、交流磁界でヒステリシスを一周する場合は、磁性体内部で磁気モーメント(スピン) がそろっている状態(磁気エネルギーが蓄えられている状態)と磁気モーメント(スピン) がバラバラ(多磁区)になる減磁過程(磁気エネルギーを失う過程)が繰り返されます。
この減磁過程で磁気モーメントのエネルギーが格子振動(フォノン)に伝えられ熱になる と考えられます。
実は、スピンダンピングの素過程はよくわかっておらず、現象論的に扱われているのが現状です。
3d遷移金属の軌道磁気モーメントはほとんど消滅しているのですが、多少は残っていることが放射光 を用いたXMCDの研究からわかっています。
磁気エネルギーはスピンからスピン軌道相互作用を通じて軌道に伝達され、さらに電子軌道は格子に 付随していますから伝達されたエネルギーは、格子に伝えられ、格子振動(フォノン)を励起する のではないかと私は考えます。
----------------------------------------------------------------------------------------
Date:Fri, 04 Nov 2016 16:46:05 +0900 Q2:東京農工大学 佐藤 勝昭 先生
お世話になっております。N高専のKです。
お忙しい中ご返事をくださり,ありがとうございます。
やっと磁気ヒステリシスによる熱についてイメージが湧きました。浅学で理解の追いついて いないところがあり,以下の疑問が残りました。
1)磁気エネルギーがスピン軌道相互作用を通じて格子振動に変換されるのは、スピン
の向きによって結晶格子が歪む磁歪現象と同様と考えてもよろしいでしょうか。
2)減磁過程において,磁気エネルギーが格子振動のエネルギーに変換されるのは,わ
かりました。ただ,磁気エネルギーが蓄えられていく過程でもスピンの向きが変化し,
格子振動を生むのではないかと思うのですが,いかがでしょうか。
3)一般的に可逆的と言われている初透磁率磁化範囲や回転磁化範囲でもスピンの
向きが変化し,ということは格子振動へエネルギーを伝えていると考えることができます
が,この場合,不可逆作用になってしまい矛盾が生じます。不可逆変化と言われる
バルクハウゼン効果のような急激な磁壁移動でのみ,格子振動を生むのでしょうか。
お忙しいところお手数をおかけしますが,何卒,ご助言をお願い申し上げます。
-----------------------------------------------------------------------------------------------------------------------
Date: Sun, 6 Nov 2016 01:04:00 +0900
A2: K君、佐藤勝昭です。
1) 基本は、スピンが格子に結びつくのは磁歪と同じですが、スピンのゆらぎによるエネルギ ーの散逸が格子の揺らぎを励起するということなので、磁歪よりもう少し動的な現象ではないでしょうか。
2) スピンの変化と格子の振動はカップルしています。いまの場合そろえ合うとき、エントロピー の減少をともなうので、むしろ、格子系を冷やすのかもしれませんね。(自信はありませんが・・)
3) 磁壁はどこにあってもポテンシャルエネルギーは同じです。従って移動にはわずかなエネルギーしか 使いませんので、多少摩擦があっても、格子系に渡すエネルギーはあまり大きくありません。
散逸は非常に少ないので、非常に速い速度で動きます。 磁壁がどこか(欠陥など)に引っかかると、そのポテンシャルエネルギーを超えて動くには大き なエネルギーが必要です。これが、バルクハウゼン損失になります。
--------------------------------------------------------------------------------------------------------------------------
Date: Mon, 7 Nov 2016 00:12:14 +0900
AA: 東京農工大学、佐藤 勝昭 先生
いつもお世話になっております。N高専のKです。
また,今回の細かな質問に関して,一つ一つ丁寧かつ分かりやすいご説明,誠にありがとうございました。 ヒステリシス損失に関して,かなり深い部分まで理解することができました。
さらに理解を深めるため,スピンと結晶格子に関する文献等の調査と内容の整理を一旦行ってみよう と思います。
今後とも,ご指導のほどよろしくお願いいたします。
------------------------------------------------------------------------
1371.シリコンナノドットの発光寿命
Date: Mon, 14 Nov 2016 22:31:26 +0900Q1: 佐藤勝昭先生、K*大学四回生のY*と申します.
(申し訳ありませんが,HPアップ時は学校名,氏名とも匿名でお願いします。)
インターネットでいろいろ調べているうちに先生のHPにたどり着き,メールで 質問をさせていただくことにしました。
現在,半導体でケイ素ナノ結晶の文献を読んでいます。
文献を読んだり、書籍で調べているのですが、電子ー空孔の光励起が起こる際の減衰速度を求める式を用いるとき、無放射再結合の求め方がわからず、メールいたしました。
実験的に求める際にはどのような計算をするのか、理論的に求めているのかなど、教えていただけないでしょうか。
突然のメールで申し訳ありませんが,よろしくお願い致します。
-------------------------------------------------------------------------
Date: Tue, 15 Nov 2016 01:06:49 +0900
A1: Y君、佐藤勝昭です。
一般に、発光の減衰はレート方程式という微分方程式を解くのですが 発光再結合の確率と非発光再結合の確率の比率で発光寿命が決まります。
非発光再結合は粒子の表面状態で決まるので実験で決めるしかありません。
周りに金属粒子があると表面プラズモンなどが関与する場合もあり、 簡単ではありません。
あなたの読んでおられるSiナノ結晶の文献を紹介いただけませんか?
---------------------------------------------------------------------------
Date:Tue, 15 Nov 2016 09:38:47 +0900
Q2: 返信ありがとうございます。
先生がおっしゃられたように、周りに金ナノロッドがあり表面プラズモンが関与している論文になっています。
タイトルは plasmon-enhanced emission rate of silicon nanocrystals in gold nanorod composite です。
よろしくお願いします。
---------------------------------------------------------------------------
Date: Tue, 15 Nov 2016 16:38:52 +0900
A2: Y君、佐藤勝昭です。 神戸大の杉本さんがBoston大で行った研究成果の論文ですね。
ACSの論文はダウンロードできませんでしたが、神戸大の紀要に収録された同じ内容の論文を読みました。
これによれは、Siナノ結晶ー金ナノロッドの系におけるフォトルミの減衰の増強は、Purcell因子による増強と、金ナノロッドの吸収に よるものとして説明でき、シリコンナノ結晶内の非発光再結合レートの金ナノロッド近接効果によるものではないと結論していますが、非発光 再結合レートの導出には触れていません。
4年生なら卒論の指導教員がおられるはずなので、詳細は、指導教員におたずねになってはいかがですか?
註:パーセル効果とは、蛍光分子の自然放出レートがそれの置かれた環境によって増強される効果(1940年代にEdward Mills Purcellが発見)です。
----------------------------------------------------------------------------
Date: Tue, 15 Nov 2016 17:11:33 +0900
AA: Yです。お忙しい中返信ありがとうございます。
担当教員の先生ともう一度話してみようと思います。丁寧に教えてくださり感謝いたします。
----------------------------------------------------------------------------
1372.棒状試料の保磁力の長さ依存性
Date: Thu, 23 Feb 2017 10:05:52 +0000Q1: 佐藤先生、C社のTと申します。(匿名希望です)
HPを拝見し質問させて頂きました。
磁性材料の評価を行っている中で、棒状サンプルの長さが短くなるごとに保磁力が増加する現象が発生しました。
(直径は同じです。)
これについて何かしらの法則があるのか、それとも測定が上手く出来ていないのかご意見を伺わせて下さい。
測定機は振動試料型磁力計になります。
又、磁化容易軸とそれ以外の測定で保磁力が異なります。
こちらについてもメカニズムがあれば教えて下さい。
以上、宜しくお願いします。
--------------------------------------------------------------------------------------------------
Date: Mon, 27 Feb 2017 01:03:00 +0900
A1: T様、佐藤勝昭です。
出張などのため、お返事が遅くなって申しわけありません。
ご質問の棒状試料の保磁力Hcの長さ依存性ですが、私にはよくわかりません。
 通常ヒステリシス曲線が形状によって変化するのは、反磁場によるものです。
しかし、添付図に示すように、保磁力は変わらず、傾きだけが変わるのです。
なぜなら、M=0においては反磁場が働かないからです。
通常ヒステリシス曲線が形状によって変化するのは、反磁場によるものです。
しかし、添付図に示すように、保磁力は変わらず、傾きだけが変わるのです。
なぜなら、M=0においては反磁場が働かないからです。反磁場が原因でないとすると保磁力の起源に遡って考えなければなりません。 磁壁移動がないとすると磁化反転は異方性磁界Hkは磁気異方性定数Kuと 飽和磁化Msを使って、
Hk=2Ku/Ms
で表されます。Hcはこの値より1桁小さいのですが、その主因は磁壁移動によると言われています。
もし、棒状試料の寸法が小さくなると、磁壁がピニングされて磁壁移動が起きにくくなるなら、HcはHkに近づくはずです。
T様の試料のピニングサイトの密度が、短い試料では高く長い試料では、低ければ、説明できると思いますが、実際にこれが起きているかわかりません。
なお、磁化容易軸では、磁壁移動が起きやすいのでHcが小さく、困難軸では磁壁移動が起きにくいのでHcが大きいことが説明できます。
--------------------------------------------------------------------------------------------------
Date: Mon, 27 Feb 2017 01:48:25 +0000
Q2: 佐藤先生
ご回答有難う御座います。
棒状サンプルについてですが、軸方向(長手方向)と90°回転方向で保磁力が異なります。
これは”磁化容易軸(長手)では、磁壁移動が起きやすいのでHcが小さく、困難軸(90°回転)では 磁壁移動が起きにくいのでHcが大きいことが説明できます”
と考え宜しいでしょうか?
以上、宜しくお願いします。
---------------------------------------------------------------------------------------------------
Date: Mon, 27 Feb 2017 13:21:02 +0900
A2: T様、佐藤勝昭です。
拙著「磁気工学超入門~ようこそまぐねの国に~」p84の式(3.20)にありますように、磁壁移動を考えない場合では
Hc=αHk-N Ms
(ここにα<1、N:反磁場係数、Ms:自発磁化)
と表され、HcはHkより小さくなっています。
ここで、αは異方性磁界の局所的な低下を表します。磁区が発生するとαが低下するのでHcも減少しますが、方向には依存しません。
反磁場係数Nは棒状試料の場合、長手方向で小さく、無限長の棒では長手方向のN=0、長手に垂直方向で大きい(N=1/2)のです。
無限長の棒の場合、
長手方向は、Hc=αHk、
垂直方向は、Hc=αHk - Ms/2
となり、長手より垂直方向のほうがHcが小さくなってしまいますね。これでは、実験を説明できません。
従って、反磁界による形状磁気異方性だけでは、T様の実験結果は説明できません。
もし、磁壁移動を妨げるピニングサイトがあると、磁壁はそこでトラップされ、磁壁移動がおきません。
ピニングサイトは、主として表面、界面に存在します。従って、垂直方向では、移動してすぐに表面とぶつかるのでピニングされやすいが、長手方向では、ピニングが起きにくいと考えられます。
短い棒状試料だと、磁壁はすぐにピニングサイトに出会うが、長いと端っこが遠く、ピニングされにくいのではないかと推察します。
従って、ご理解のように磁壁移動の起きやすさがHcの低下の原因であるというご理解でよいと思います。
--------------------------------------------------------------------------------------------------------
Date: Tue, 28 Feb 2017 09:03:23 +0000
Q2: 佐藤先生
少し気になった点がありますので質問させて下さい。
棒状磁石の飽和磁化Msですが、短くなると反磁場+形状効果で小さくなると思います。
その場合、Hk=2Ku/MsにおいてHkは大きくなりますので、相関するHcも大きくなります。
ただし、Hc=αHk-N Msにおいては、Nが増加するためマイナス側へも動きます。
上記から、状況によっては反磁場の影響で保磁力は増加すると考えても良いのでしょうか?
磁気の勉強はしていますが理解に苦しんでいます。
------------------------------------------------------------------------------------------------------------
Date: Tue, 28 Feb 2017 22:49:27 +0900
A2: T様、佐藤勝昭です。
Msは磁性体が本来もつ飽和磁化なので、反磁場の影響を考えません。
従ってMsは形状に依存しません。
------------------------------------------------------------------------------------------------------------
Date: Fri, 3 Mar 2017 08:38:41 +0000
AA: 佐藤先生
内容を理解するのに時間が掛りご返信が遅く申し訳ありません。
測定装置メーカさんにお話を伺った結果、正確な測定が出来ていない可能性を指摘されました。
丸棒を短くしていくと保磁力が上がる現象は今一度精査します。
いろいろ有難う御座いました。
大変勉強になりました
---------------------------------------------------------------------------------------------------------------
1373.選択的光吸収材
Date: Wed, 01 Mar 2017 10:55:08 +0900Q: 佐藤勝昭様
はじめまして。ホームページを拝見し、ご連絡差し上げました。
K社 Oと申します。
お手数をおかけしますが、Web掲載の際には会社名、氏名ともに匿名にてよろしくお願いいたいます。
早速ですが、選択的光吸収材に関心があり調査を行っています。
例としては添付しております論文のようなものです。
金属ナノ粒子をセラミック中に分散させたサーメットが広く研究されていますが、 構造は同じまま、その分散粒子を金属ではなく、酸化物や非酸化物系のセラミックで 代替しようと考えています。
また、添付資料のFig.4に載っているような反射率をカットオフ波長でさらに急峻に変化 させたいと考えており、その因子として個人的には分散粒子の誘電率変化を急峻にする ことが重要ではないかと考えています。
したがって、粒子の材料としては金属のように誘電率が急峻に変化するような材料が適していると考えています。
そこで、下記の内容に関して質問があります。
1)誘電率が急峻に変化するような材料はセラミックの中ございますでしょうか。
2)誘電率の変化が何に起因しているか
3)誘電率を急峻に変化させられる可能性のある手法(構造、バンドなど)
お忙しいところ、大変恐縮ですがご教授いただければ幸いです。
----------------------------------------------------------------------------------------------------------
Date: Thu, 2 Mar 2017 07:33:19 +0900
A: O様、佐藤勝昭です。
メールありがとうございます。ご質問にお答えします。
1) 誘電率が急峻に変化するような材料はセラミックの中ございますでしょうか。
図2の短波長側の透過率の急峻な減少はYSZの吸収端(バンドギャップ)によるものです。
(これは、誘電率で言えば、虚数部の変化に相当します。)
直接遷移型半導体であれば同様の短波長側の急峻な透過率変化が見られます。
一方、図4の長波長側の反射率の変化は、サーメットに含まれる金属の自由電子による プラズマ振動のため、誘電率の実数部が負になることが原因です。これは、金や銀の 色をもたらす選択反射と同じ原因です。従って、自由電子の少ないセラミクスでは このような変化は期待できませんが、高濃度に不純物をドープしたいわゆる縮退半導体 であれば、赤外部に同様の負の誘電率が現れます。
これとは別の原因の高い反射率は、NaClなどイオン結晶に見られるレストストラーレン 反射があります。これは、格子振動によるものです。NaClはセラミクスとは呼べないですね。
2)誘電率の変化が何に起因しているか
上に述べたように短波長側は半導体のバンドギャップ、長波長側はプラズマ振動 や格子振動によるものです。
3)誘電率を急峻に変化させられる可能性のある手法(構造、バンドなど)
短波長側は、直接遷移型半導体の吸収端を使えばよいでしょう。
長波長側は、縮退半導体の自由電子プラズマを使えばよいでしょう。
あるいは、イオン結晶のレストラーレン反射を使えばよいでしょう。
-------------------------------------------------------------------------------------------------------------
Date: Thu, 02 Mar 2017 14:08:28 +0900
AA: 佐藤勝昭様
早速お答えいただきありがとうございます。
下記の内容に関してよく理解できました。
長波長側の誘電率を急峻に変える方法は、やはり自由電子プラズマを利用する方法が適しているのですね。
レストストラーレン反射を利用する方法についても調査してみます。 不明点があれば、再度質問させていただこうと思いますので、今後とも何卒よろしくお願い致します。
-------------------------------------------------------------------------------------------------------------
1374.印刷インクの高周波による変化は起きるか
Date: Thu, 08 Jun 2017 09:54:18 +0900Q: 佐藤先生
お世話になります。K'社のO'と申します。
高周波電界(数100kHzのパルス状)を利用して、容器の表面 に電極を貼り付けて液体のレベルを測定する製品を開発し、販売 をしているメーカです。
お客様は印刷用のインクのレベル検出をされていますが、検出 そのものは問題ありませんが、使用し続けているとインクが変 質するので困っているとのことです。容器はガラスです。印加 電圧は3Vです。
お客様も、このセンサが原因であるとは結論付けてはおられま せんが、高周波電界で液体が変質する可能性があるのか、問題 ないのか教えていただきたくメールさせていただきました。
インターネットなどでは的確な情報が得られませんでした。
よろしくお願いします。
----------------------------------------------------------------------------------------------------------------
Date: Fri, 9 Jun 2017 15:19:44 +0900
A: O'様、佐藤勝昭です。
印刷用のインクの化学組成がわかりませんが、一般的には顔料を溶剤に分散させた コロイドあるいはエマルジョンで、粘性を高めるためにパラフィンなどゲル状の物質 を加えているようですね。周波数を変えながら、交流インピーダンス特性を測定し、 cole-cole plotをすれば、劣化にともなう変化を見ることが出来ますが、調べた限り では、下記論文しか見当たりませんでした。
佐藤正壽 他: W/O エマルジョンインキの交流インピーダンス法による安定性評価: 日本印刷学会誌 31 No.2 (1994)pp24-28
この論文は、攪拌によって粘度が上がること、水相比率ともに低周波抵抗が下がるが、 高周波抵抗率は一定値をとること、60℃で保存した場合、交流インピーダンスの実部 と虚部をプロットしたものは、エマルジョンの水相合一と、水相分子同士の接触が起 きていることが見られています。
このように、高周波電界は、インクの経時変化をインピーダンス観察するために 使うのですから、高周波によって変化が起きることは考えられません。
インクの変質は、別の要因(光劣化、経時変化)によるものと考えられます。
-----------------------------------------------------------------------------------------------------------------
Date: Mon, 12 Jun 2017 09:12:29 +0900
AA: 佐藤先生
早々にご指導いただきまして、ありがとうございます。
お礼のメール、遅くなり申し訳ありません。
「インクの経時変化の観察に高周波を使用するので。高周波電界でインクに変化 がおこることは考えられない」とのことで安心しました。
お客様に伝えたいと思います。
ご紹介の論文も拝見したいと思います。
お忙しい中を調査までしていただき、本当にありがとうございました。
----------------------------------------------------------------------------------------------------------------
1375.「金属の電子構造_触媒作用の理解のために」への質問
Date: Wed, 23 Aug 2017 12:54:45 +0900Q1: 佐藤様、初めまして、H(株)のMと申します。
 先生の著作「金属の電子構造_触媒作用の理解のために」の中でどうしてもイメージをつかめない部分があり、1点質問をいたします。
先生の著作「金属の電子構造_触媒作用の理解のために」の中でどうしてもイメージをつかめない部分があり、1点質問をいたします。お忙しいところ申し訳ありません。ご回答をお願いいたしたく存じます。
2ページ目
「d状態がフェルミ準位に対して上の方にシフトする」とはどのようなイメージなのでしょうか。
(図3においてdバンドセンターが上に移動するということなのでしょうか。そうしたら反結合軌道の占有は増加するのではないのでしょうか。) 以上です。どうぞよろしくお願いいたします。
------------------------------------------------------------------------------------------------------------------
Date: Wed, 23 Aug 2017 14:21:28 +0900
A1: M様、佐藤勝昭です。
 添付のような図を描いてみました。
添付のような図を描いてみました。dバンドの全幅が変わらないとすると、センターのエネルギーが上がると右図のように反結合軌道の非占有部分が増加します。
--------------------------------------------------------------------------------------------------------------------
Date: Wed, 23 Aug 2017 16:02:04 +0900
Q2: 佐藤様、図の添付、ありがとうございました。こちらについては理解できました。
 お忙しいところ誠に恐れ入ります。あと四点、質問ががございます。
お忙しいところ誠に恐れ入ります。あと四点、質問ががございます。ご回答のほど、よろしくお願いいたします。
・P.3 図4の解釈について
1. ここで用いているdバンド中心とはP.2図3右側のグラフ点線で示してあるものでしょうか。
それとも図3中央の混成軌道におけるdバンドセンターなのでしょうか
2. dバンドセンターの位置(横軸)が左に行くほど反結合状態の割合が増加し、
触媒表面に酸素が結合しにくくなるという解釈でよろしいでしょうか。
(例えば、Pt,Niを基準とした場合、Pt,Tiは表面に酸素が結合しにくい(吸着が起こりにくい)ため、Pt,Niに比べ活性が下がる。
PtはPt,Niに比べ酸素との結合力が高いため活性が下がる。)
3. 縦軸(単位: eV)は活性の高さだと思うのですが、活性の高さを表すのに交換電流密度(単位:A)を用いた文献も見かけます。
単位が異なりますが同じ意味でしょうか。
4. P.2図2と比較して縦軸の値が異なるように見える
(Pt,Niにおいて図2では-0.26 eV ,図3では+0.03 eV)のですが、図2と図4は異なるものなのでしょうか。
以上です。どうぞよろしくお願いいたします。
------------------------------------------------------------------------------------------------------------------
Wed, 23 Aug 2017 18:05:40 +0900
A2: M様、佐藤勝昭です。
私は、燃料電池の専門家ではなく、依頼を受けて、電子構造と触媒活性の
関係の論文をにわか勉強で読んだので、記述が不十分になったことをお詫びします。
ご質問ですが、
1.ここで用いているdバンド中心とはP.2図3右側のグラフ点線で示してあるものでしょうか。
それとも図3中央の混成軌道におけるdバンドセンターなのでしょうか
A1. 図3の中央図の混成軌道のバンドセンターであると考えています。(図3右図は混成前のPtのdバンド中心です)
2. dバンドセンターの位置(横軸)が左に行くほど反結合状態の割合が増加し、触媒表面に酸素が結合しにくくなるという解釈でよろしいでしょうか。
A2 左に行くほど、深くなるので、反結合軌道の占有が増えます。ご解釈のとおりです。
3. eVで表した活性と交換電流密度は同じか
A3 専門家に聞いてください。
4. 図2と図4は異なるものなのでしょうか。
A4 これもよくわかりません。
原論文を丁寧に読み比べる必要がありそうですが、傾向だけと考えてください。
--------------------------------------------------------------------------------------------------------------------
Date: Thu, 24 Aug 2017 08:21:48 +0900
AA: 佐藤様
お忙しいところ、ご回答いただき誠にありがとうございました。
このようにご都合をつけて下さった事、大変感謝しております。
また先生の著書を読む事がありましたら質問をする事があるかもしれません。
その際はご対応いただけますと幸いに存じます。
今後とも、どうぞよろしくお願いいたします。
それでは、失礼いたします。
----------------------------------------------------------------------------------------------------------------------
1376.オゾンの吸収係数
Date: Sun, 3 Sep 2017 07:18:28Q: 佐藤勝昭教授、
Oと申します。定年退職後、派遣として設計の仕事を行っています。
携わっている装置が、開発機なので会社名は申し上げられません。
佐藤教授のHP 「基礎から学ぶ光物性第2章 (2)」 について、
・HPでは、
結晶中 ( N=2.5+0.5i ) の光の挙動についての記述ですが、
大気中では、 ( N=1.0+1.0i ) としてよいのですか。
・大気中に存在する、酸素・オゾン・水蒸気の紫外線C領域の吸収係数を算出しようとしています。
例えば、オゾンは大気圧状態(1,013HPa)に換算して 3mm の厚さにしかなりませんが、殆どの紫外線Cを吸収しているとあります。(気象庁 HP)
透過率 10% とすると、 吸収係数 7.68cm-1 の計算になります。濃度 10ppm の場合は、 吸収係数 7.68E5cm-1 でよいのですか?
濃度の逆数をかけています。
・大変失礼ですが、上記のHPの 83行目は計算結果が違っていると思います。
吸収係数α=4πκ/λ =2.51×107[m-1]=2.51×105[cm-1]
I (x)=I (0)×e-12.56= 3.50963×10-6
となり、強く減衰します。の部分ですが、
吸収係数α=4πκ/λ =1.26×107[m-1]=1.26×105[cm-1]
ではありませんか。
----------------------------------------------------------------------------------------------------------------
Date: Sun, 3 Sep 2017 09:35:58
A: O様、佐藤勝昭です。
私の講義資料をご参照頂きありがとうございます。
(1)空気の屈折率の実数部は、正確には50nmにおいて1.0002790ですが細かい話をしないときは1.0としてよいでしょう。
なお、虚数部は、ご指摘の1.0でなく0.0としてN=1.0+i0.0としてよいと思います。
(2)私は、気体の吸収については、専門外です。
オゾンのUV-Cの波長での吸収係数ですが、NOAA Earth System Research LaboratoryのサイトにDobson装置で測定した値が表に収録されています。
測定によって違いますが、およそ0.8(atm-cm)-1です。 なお、atm-cmというのは、地上から大気上端までの気柱内のオゾンを標準状態(0℃,1atm)としたときの厚さです。
・10ppmのとき、濃度の逆数をかけてよいか、専門外なので分かりません。
この道の研究者に聴いて下さい。
(3)Webの計算間違いについてご指摘ありがとうございます。Webを修正しました。
----------------------------------------------------------------------------------------------------------------
Date: Mon, 4 Sep 2017 02:54:35
AA: 佐藤勝昭教授
早速の回答ありがとうございました。
-----------------------------------------------------------------------------------------------------------------
1377.授業資料「磁気光学入門第4回」への質問
Date: Tue, 12 Sep 2017 15:18:05Q: 佐藤様、 突然申し訳ありません。
C社Aと申します。 磁気光学のファラデー回転角計算についてメールさせていただきました。
最近、弊社で磁気光学関係の研究をはじめました。
弊社の中では、光関係に詳しい者は無く手探りで、研究を行っているところです。
現在は佐藤様のホームページで勉強をさせて頂いております。
とても参考になり助かっております。ありがとうございます。
そこで、「授業資料・パワポ」の中の「磁気光学入門」で1つ質問があります。
-----------------------------------質問内容------------------------------------------------------
【第4回 電磁気学に基づく磁気光学の理論 (2)マクスウェルの方程式】 のファラデー回転角計算の具体例についてです。
ファラデー回転角の計算を試しに行ってみたのですが、計算結果が合わないようで困っております。
初歩的な質問で申し訳ありませんが、お答えして頂ければ幸いです。
「やや抽象的な式が続いたので、多少具体的な例を示しておこう。
図3.6にはビスマスを添加したYIG(イットリウム鉄ガーネット:Y3-xBixFe5O12)の誘電テンソルの対角 および非対角成分の実数部および虚数部のスペクトルを掲げる。2この物質はフェリ磁性を示す絶縁 性結晶で、2.5 eV(~500 nmの波長に相当)以下の光エネルギーに対して殆ど透明であることが 図3.6(a)のε"xxのスペクトル(光の吸収を表す)から知られる。ヘリウムネオン・レーザ光(波長633 nm ~1.9 eV)を用いた場合には、図よりε'xx=5.3、ε"xx=0と読み取れる。これから光学定数を計算すると n=2.3とκ=0である.したがって,式(3.56)が成立する。図3.6(b)から,ε'xy~0、ε"xy~0.005 と読み 取れるので,上式からηF~0、θF~-1.1×102(ラジアン)=-6.3×103(度)を得る」
--------------------------------------------------------------------------------------------------------------
以上が記述してあったファラデー回転角の解説です。
計算で利用した式は(3.56)です。
ε´xy = 0、ε´´xy = 0.005、n = 2.3、k = 0(ε´xx = 5.3、ε´´xx = 0を(3.39)に代入)
を(3.56)に代入すると
η=0、 θF = (ω×0.005×ζ)/(2×c×2.3)
となりました。
ここで、恐らくωとζ、cの値を入れるのを間違えたと考えています。
c ≒ 300000×103[m/s]
ωはレーザーの波長(633nm)と光速cから換算で求めるのでしょうか?
ζは試料の厚さだと思うのですが、光と磁気の教科書の方に例題の記述があるのでしょうか?
-----------------------------------------------------------------------------------------------
とても初歩的な質問で大変申し訳ありません。
お手数おかけし申し訳ありませんが、ご回答いただければ幸いです。
以上、宜しくお願い致します。
------------------------------------------------------------------------------------------------------------
Date: Tue, 12 Sep 2017 18:14:43 +0900
A: A様、佐藤勝昭です。
厚みが書いてなかったですね。厚みζ=1cmで計算しています。
ΘF=ωε"xyζ/2cn
角振動数ω=2πc/λなので
ΘF=πε"xyζ/nλ
波長λ=633nm=6.33×10-5cm
屈折率n=2.3
ζ=1cm
ε"xy=5×10-3
を代入すると
θF=3.14×5×10^-2 ×5×10-3/2.3×6.33×10-5=1.1×102
となります。単位長さ(cm)あたり110radです。
---------------------------------------------------------------------------------------------------------------------
Date: Tue, 12 Sep 2017 18:28:27
AA: 佐藤様
お早いご回答、誠にありがとうございます。
厚み等の情報ありがとうございます。
計算等も詳しく記述して下さりありがとうございました。
------------------------------------------------------------------------------------------------------------------------
Date: Thu, 21 Sep 2017 16:35:59
Q2: 以前、ファラデー回転θFの計算についてご教示いただき誠にありがとうございました。
また伺ったファラデー回転の計算でご確認したいことがあり連絡いたしました。
基本的かつ大変失礼な質問となってしまい申し訳ありません。
以下のθFの計算なのですが、5×10^-2という数字は、nやε´xxでいうとどの値となるのでしょうか?
【θF=3.14×5×10^-2 ×5×10^-3/2.3×6.33×10^-5=1.1×10^2】
ζ=1cmは単位系がcmで揃っていると思ったので除外いたしました。
ちなみに5×10^-2を含めるとθFが5.39という値になってしまいます。
含めなければ 1.07×10^2 ≒ 1.1×10^2になります。
大変失礼ですが、もしかすると誤記という事なのでしょうか?
------------------------------------------------------------------------------------------------------------------------
Date: Sun, 24 Sep 2017 19:20:13
A2: A様、佐藤勝昭です。
混乱させてごめんなさい。授業資料が間違っています。
(授業資料は、間違いがある場合、授業中に訂正していました。)
ε"xyのスペクトルは第10回の資料、光と磁気第6章にあります。
これから読み取れる数値は、ε"xy~0.05です。(ε"xy~0.005は間違いです)
従って、5×10^-2の数値がε"xyを表しています
ΘF=πε"xyζ/nλ
ここに、π=3.14、ε"xy~0.05、ζ=1cm、n=2.3、λ=633nm=6.33X10^-5cm
を代入すると、
ΘF=3.14X5X10^-2/(2.3X6.33X10^-5)=1.57X10^3/14.6
=(1.57/1.46)X10^2=1.08X10^2 (rad)
--------------------------------------------------------------------------------------------------------------------------
Date: Mon, 25 Sep 2017 09:59:07
AA1: 佐藤様。
いつもお世話になっております。Aです。
授業資料の解説、誠にありがとうございます。
此方の勉強不足で、大変初歩的な質問になってしまい申し訳ありませんでした。
また何か疑問点など出てくるかと思いますが、その際には佐藤様のお力をお借り できれば幸いです。
大変忙しい時期でのご回答ありがとうございました。
以上、宜しくお願い致します。
-----------------------------------------------------------------------------------------------------------------------------
Date: Fri, 6 Oct 2017 18:16:36
Q3: 佐藤様。
度々申し訳ありません。
YIGのファラデー回転について、印加磁場と回転角の関係ついて知りたく連絡致しました。
回転角の印加磁場依存性をシミュレーションをしてみようと思い調査しております。
一般的にはベルデ定数と磁場と試料の長さを掛けて、回転角を求めるという式が あります。
今回実験でレーザー波長が1310nmと1550nmを使う予定なのですが、ベルデ定数が分からないため計算に詰まっている状態です。
そこで以前、計算方法をご教示して頂いた誘電率の対角成分を使って計算できるかと思い調査しております。
ΘF=ωε"xyζ/2cn
佐藤様の磁気光学講義資料では、磁化があるときの誘電率テンソルの表記の内容があるため、それがヒントかと思い調査しています。(磁気光学の基礎と最近の展開(2)) 例えば誘電率スペクトルと印加磁場を結びつける何らかの関係式等が有るのでしょうか?
それが分かれば回転角の印加磁場依存性が分かりそうなため、お知恵をお貸し頂けると幸いです。
短い期間に何度も質問申し訳ございません。
以上、宜しくお願い致します。
-------------------------------------------------------------------------------------------------------------------------
Date: Sat, 7 Oct 2017 07:47:20
A3: A様、佐藤勝昭です。
 「誘電率スペクトルと印加磁場を結びつける何らかの関係式等が有るのでしょうか?」というご質問ですが、答えはNOです。
「誘電率スペクトルと印加磁場を結びつける何らかの関係式等が有るのでしょうか?」というご質問ですが、答えはNOです。添付図は、MOD法でガラス基板に成膜した面直磁化をもつYIG薄膜のファラデー回転の磁界依存性です。
これを見れば、ファラデー回転は磁界に対してヒステリシスを持ち、比例関係に無いことがおわかりいただけるでしょう。
もし、成膜を工夫して面内磁化のYIG薄膜を作れば、磁界に比例して磁化が立ち上がりますので、飽和するまでは比例します。
飽和する磁界がわかれば、見かけのベルデ定数が定義できます。
-------------------------------------------------------------------------------------------------------------------------
Date: Wed, 11 Oct 2017 09:39:36
Q4: 佐藤様。Aです。
貴重なご意見およびデータありがとうございます。
またお返事が遅くなり申し訳ありません。
磁気光学関係は勉強不足だと痛感致しましたので、佐藤様著書の光と磁気を購入いたしました。
今後、そちらの参考書を中心に学んでいこうかと思います。
差し支えなければなのですが、頂いたデータのYIG膜厚を教えて頂くことは可能でしょうか?
可能であれば見かけのベルデ定数を検討してみようかと思います。
勿論実験データの為、データの提供が難しい場合は問題ありません。
ご多忙のところ申し訳ありませんが宜しくお願い致します。
以上、宜しくお願い致します。
----------------------------------------------------------------------------------------------------------------------------
Date: Fri, 13 Oct 2017 13:09:33 +0900
A4: 様、佐藤勝昭です。
私が東京農工大に研究室を持っていた頃の助教で、現在長岡技術科学大学教授の石橋隆幸先生が、ガーネットの磁気光学を引き続き研究しています。
石橋先生に伺ったところ下記の回答がありました。
================================
ヴェルデ定数としては整理していませんが、添付の実験データから見積もると次のようになります。
ファラデー回転角だけでなく、飽和磁場も関係するので、Biの組成に比例していません。
飽和磁場がばらついているのは、それぞれの組成での焼成条件が最適化されていないことが原因かもしれません。
| 試料 | θ(degree/um) | V(min/A) | V(degree/kOe・μm) | 測定波長(nm) |
|---|---|---|---|---|
| BIG | 32.0 | 17200 | 22.9 | 528 |
| Bi2.5YIG | 21.4 | 10800 | 14.3 | 528 |
| Bi2YIG | 16.9 | 11100 | 14.8 | 517 |
| Bi1.5YIG | 8.38 | 5020 | 6.66 | 517 |
Y3Fe4GaO12は、作製できるのですが正確な膜厚の評価を行っていないので、 数字は出せませんが、ファラデー回転角から予想すると Bi1.5YIGの20分の1以下になるのではないでしょうか。
=================================
さらに、詳しいことは、石橋先生に直接聞いて下さい。
-----------------------------------------------------------------------------------------------------------------------------------
Date: Fri, 13 Oct 2017 18:03:14
AA: 佐藤様。C社のAです。
文献およびデータ、誠にありがとうございます。
また、ガーネットの磁気光学を研究されている方をご紹介して頂き誠にありがとうございました。大変助かりました。
今回、データの提供などとても親身に対応して頂き、誠にありがとうございました。
取り急ぎ連絡申し上げます
------------------------------------------------------------------------------------------------------------------------------------
1378.金属の誘電率はマイクロ波領域でも負になるか
Date: Wed, 18 Oct 2017 13:43:47Q: 佐藤勝昭先生
T大学Yと申します。以前、いろいろ質問にお答えいただきどうも有り難うございました.
ところで、金属の誘電率の件で、再度ご質問させて頂きたいのですが、
「ドルーデモデルは、マイクロ波周波数でも成り立ち、実部の値が負であるのか」という件です。
金属の誘電率を扱う理論として、外部から電場等のポテンシャルが与えられ、電子がそれに応じて運動する場合、 波数q、角振動数wの外部摂動V(q,w)に対する電子系の応答は、誘電関数eps(q,w)により記述され、 これを求めるLindhardの理論があります。(キッテル、ザイマン固体物理参照)
これによると、電子気体の2つの極限では、
(lamb=4*pai*e^2*N(epsF), N(epsF)はフェルミ準位での状態密度として)
eps(q,0) = 1 + lamb^2/q^2 (1) , eps(0,w) = 1 - wp^2/w^2 (2)
となってます。
(2)式は、文字通りプラズマ振動数以下で誘電率が負になる事を示しているのですが、 マイクロ波の波数も光に比べれば、非常に小さい(qは小さい)ため、(1)式では負ではなく、 相当大きな正の値になるのではないかと考えられます.
またLindhard理論とDrude理論の比較を行なった 文献もあります。
ただし、ここではeps-infiniteという値を導入して、誘電率が負にはなっていないようです
この辺の件に関し、御意見等、ご教示いただければ幸甚に存じます.
----------------------------------------------------------------------------------------------------------------------------------------
Date: Wed, 18 Oct 2017 16:06:21
A: Y様、佐藤勝昭です。
論文を読みました。コメントは添付のファイルに書きました。ナノ構造など電磁波の 波長が十分大きい極限では、低周波でLindhardモデルがよい近似となるのですね。
ここでは誘導に近似を使っていますから、いろんな系でこれが成り立つのかは、実証が必要でしょうね。
----------------------------------------------------------------------------------------------------------------------------------------
Date: Wed, 18 Oct 2017 18:15:44
AA. 佐藤勝昭先生
早速ご返信いただき、大変感激しております.
Lindhardによる誘電関数に関しては具体的な解析式もあり、
これが、いろいろな系で(金属 vs.マイクロ波において、どのようなqとwを選ぶか)どうなるのか調べてみたいと思っております。
しかしながら、なかなか単純ではなく、金属と言う事はどういう条件のことを言うのかとか、 縦と横の電磁場での違い等も書かれております。その辺どう考えれば良いのかなど、 方針につきまして、ご教示いただければと存じます.
-----------------------------------------------------------------------------------------------------------------------------------------
1379.LED用光ガイドをプラスチックで作りたい
Date: Fri, 8 Dec 2017 12:21:03Q: 佐藤様、E社のSと申します。
 今回の質問は透明なアクリル、又はポリカーボネイトでLEDの光を下から入れ、手前に出したいのですが、
図の形状で問題なく光るのかどうか教えて頂きたくメールさせてもらいました。
今回の質問は透明なアクリル、又はポリカーボネイトでLEDの光を下から入れ、手前に出したいのですが、
図の形状で問題なく光るのかどうか教えて頂きたくメールさせてもらいました。切削ではなくインジェクション成型で作る予定です。
A,B共に光らないのであればどこを工夫すれば光るのかご教授いたただければ幸いです。
宜しくお願い致します。
---------------------------------------------------------------------------------------------------------------------------------------------
Date: Mon, 11 Dec 2017 12:14:17 +0900
 A: S様、佐藤勝昭です。 出張のためお返事が遅くなりました。
A: S様、佐藤勝昭です。 出張のためお返事が遅くなりました。いただいた図では、光が漏れてしまうと存じます。
添付の図に示す様に、角を45度にカットすれば全反射するので、 よいのではないでしょうか。やってみてください。
-----------------------------------------------------------------------------------------------------------------------------------------------
Date: Mon, 11 Dec 2017 12:19:55
AA: 佐藤さま、返信ありがとうございます。
早速、添付の図に従い、やってみようと思います。
ありがとうございました。
------------------------------------------------------------------------------------------------------------------------------------------------
1380.金属薄膜の仕事関数の膜厚依存性
Date: Sat, 16 Dec 2017 07:38:50Q: 佐藤先生、T大学4年のAと申します.
最近,授業にて金属の仕事関数について学びました.仕事関数の定義や測定方法など,基本的なことは理解しているつもりです.
質問内容は,金属の仕事関数は,金属の膜厚によって変化するのか?ということです.
また,変化するならば,どのような傾向があるのかを知りたいと考えております.
授業の中で,金属の仕事関数は,結晶方位によって異なるという説明を受けました. 従って,絶対的な物理量ではなく,様々な条件によって変わりうる値だと理解しています.
私の考えでは,膜厚が薄い方が,電子を束縛するエネルギーが低いと考えられるので, 仕事関数が小さくなるのでないかと考えております.
お忙しいとは思いますが,佐藤先生のご意見をお伺いせてください.
宜しくお願い申し上げます.
-------------------------------------------------------------------------------------------------------------------------------------------------
Date: Sat, 16 Dec 2017 14:39:05
A: A君、佐藤勝昭です。 金属薄膜の仕事関数の膜厚依存性は、過去に研究があります。
例えば、J. Vancea, G. Reiss, D. Butz and H. Hoffmann: "Thickness-Dependent Effects in the Work Function of Polycrystalline Cu-Films", Europhysics Letters, Vol.9, No.4 (1989) 379
この論文では、成膜中ケルビンプローブ法で測定しています。
それによれば、あなたの推察通り、膜厚の増加とともに0.1eVばかり仕事関数 が増加することを観測しています。詳細は、上記論文を読んでください。
--------------------------------------------------------------------------------------------------------------------------------------------------
1381.温度依存性のない発光スペクトル
Date: Wed, 27 Dec 2017 17:16:56Q1: 佐藤様、突然失礼致します。
私、N*大学M1のA*と申します。HPをみて質問させて頂きました。匿名希望で宜しくお願い致します。
大学院では、主に発光について研究を行っております。
低温PL測定を行った結果について質問です。
試料を低温(20K)に冷やしていくと、PL強度は、どんどん増加していきました。しかし、規格化すると、室温と低温のPLスペクトルがシフト等もせず、スペクトルがピッタリ一致しました。何回か実験を行っても、同じような結果になります。様々な論文を読みましたが、そのような結果の論文は見つけられませんでした。
これについてもし知見があれば、ご助言宜しくお願い致します。
-------------------------------------------------------------------------------------------------------------------
Date: Wed, 27 Dec 2017 17:30:58
A1: A君、佐藤勝昭です。
M1だったら、指導教員がおられるでしょう。
私が指導教員だとしたら、学生が実験結果について自分を差し置いて他機関の先生に 質問したとすると、自分は低く見られているんだなといやな気分になるでしょうね。
まずは、指導教員の先生に聴くべきです。先生が答えられないならば改めて先生の 許可を得て質問してください。
------------------------------------------------------------------------------------------------------------------
Date: Wed, 27 Dec 2017 17:38:10
Q2: 指導教員に実験結果を報告し、こうだと思うという考えを頂いたのですが、自分の中でその答えが納得できなかったため、 他の方の意見もお聞きしたいと考えメールしました。
------------------------------------------------------------------------------------------------------------------
Date: Wed, 27 Dec 2017 18:37:57
A2: A君、佐藤勝昭です。
ヒントを上げましょう。
半導体のバンドのように電子状態が結晶全体に広がっているような場合、スペクトルは温度に依存します。
しかし、希土類イオンのf電子系のように、電子状態が局所的であれば、温度による影響をほとんど受けません。
量子ドットでも温度依存性が少ないです。
PLスペクトルの温度変化は、物質依存性が大きいのです。
------------------------------------------------------------------------------------------------------------------
Date: Sat, 30 Dec 2017 15:03:18
AA: 佐藤様、返信遅くなり申し訳ありません。
ヒントを基にもう少し考えてみたいと思います。ご教授、ありがとうございます。
------------------------------------------------------------------------------------------------------------------
1382. La-BaZrO3のドーピング
Date: Thu, 25 Jan 2018 18:20:21Q: 東京農工大学 名誉教授 佐藤 勝昭 先生
突然のメール失礼いたします。K*大学大学院工学府の修士課程2年生M*と申します。
指導教官と話し合って実験を進めるうえで解決できない疑問にあたってしまい、指導教官から佐藤先生に聞いてみてごらんなさいという助言を頂き質問させていただくことにしました。
指導教官の許可はありますが匿名でお願い致します。
現在ペロブスカイト構造の材料を積層させた薄膜太陽電池の研究を行っています。
そのうちの一つの項目として透明電極材料の新規開発においてLaをドープしたBaSnO3(LBSO)膜の研究報告(Appl. Phys. Lett. 103, 042105 (2013))を参考にし、 BaZrO3(BZO)にLaをドープしてLBZOにできないかと考えていますが良い結果を得ることができていません。
LBSOが導電性をもつ理由としてSn-OハイブリダイゼーションがSnの5s軌道由来の伝導帯底(CBM)を提供しかつ、約0.2m0という低い有効質量を有する分散帯を生じさせるとあります。
基底状態においてSnの電子配置が(Kr)4d(10)5s(2)5p(2)でZrの電子配置は(Kr)4d(2)5s(2)であります。以上のことからBZOにLaをドープすることを決めました。
基板も格子マッチングの良いものを使用し、成膜条件はJournal of Crystal Growth Volume 300, Issue2, 15 March 2007, Pages 478-482を参考にしてPLD法で作製しエピ成長をさせています。
しかしながら導通を得ることができませんでした。超高真空~極高真空下で製膜すると酸素欠損のおかげなのかわずかに導通を得ることができます。
以上のことを踏まえてさせていただきたい質問は、なぜZrでは導通を得ることができないのか?です。
修士の途中までは全く別の方向を目指し、違う物質の塗布性の向上と結晶性の向上をめざしていたため電子系の理論について疎いため参考にするべき図書などがございましたらご紹介いただけると幸いです。
何卒よろしくお願い致します。
------------------------------------------------------------------------------------------------------------------
Date: Thu, 25 Jan 2018 21:07:38
A: M*君、佐藤勝昭です。
 BaZrO3はプロトン(H+)伝導材料としてよく知られていますが、電子の伝導性については、余りよく知られていません。
BaZrO3はプロトン(H+)伝導材料としてよく知られていますが、電子の伝導性については、余りよく知られていません。BaSnO3の場合はSnの外殻電子は3d10が閉殻になっているので5s25p2が伝導帯に関与します。
一方、BaZrO3の場合、Zrは4d遷移金属で外殻電子は4d25s2なので、有効質量の大きい4d電子が伝導帯の底を構成し、O2p価電子帯との間に4.8eVのバンドギャップがあります。
バンドギャップが大きいと不純物準位のエネルギー準位が深いので、キャリアが活性化しにくいので、キャリア密度が十分とれません。
導電率σはキャリア密度n, 移動度μを使って、σ=neμと書けます。伝導帯の有効質量m*が大きいと移動度はμ=eτ/m*と書けるので小さく、nもμも小さいからσも低いのです。
従って、LBZOで透明導電膜を狙うのはむずかしいのではないでしょうか?
(なお図は、K.Maeda: Physical Chemistry Chemical Physics Issue 26, 2013によります。)
------------------------------------------------------------------------------------------------------------------
Date: Fri, 26 Jan 2018 10:44:38
AA: 東京農工大学 教授佐藤 勝昭 先生
大変お世話になっております。K*大学修士2年のM*です。
すぐに質問に回答くださりありがとうございます。
理解することができました。
別のものを検討していきたいと思います。
------------------------------------------------------------------------------------------------------------------
1383.光・X線の侵入長の波長依存性
Date: Fri, 15 Jun 2018 15:05:46Q: 佐藤勝昭先生
はじめまして。Y*大学のF*と申します。 先生が開設されております「物性なんでもQ&A}と見まして、 私の素朴な疑問を解決して下さるかもしれないと思い、メールを書かせて頂いております。私は物理に 詳しくないため、教えて頂けますと助かります。どうぞ、宜しくお願いいたします。
光は波長が短い方が、物質への侵入長が短くなると聞きます。一方、X線に関しては、波長が短い方が、 物質への侵入長が長くなると聞きます。光もX線も電磁波なのですが、なぜ、そのような違いが出てくるの でしょうか。それを解決するために、以下のことをお聞きしたく思います。
(1)光の波長が短い方が、物質への侵入長が短くなる理由は何でしょうか。波長が短い方が、散乱し やすくなるので、それが効いているとも思いますが、それは多結晶のように物質内に界面がある場合など、 散乱が起きる場合での話であり、単結晶では散乱は関係がないように思えます。光の波長が短い方が、 光の吸収率が高くなることにより、侵入長が短くなるのでしょうか。もし、そのようでしたら、物質のバンド ギャップエネルギーを超えない範囲内では、侵入長の波長依存性は、ほとんどないと考えても良いのでしょうか。
(2)X線の波長が短い方が、物質への侵入長が長くなる理由は何でしょうか。
(3)X線は、明らかに物質のバンドギャップを超えるエネルギーを持つ電磁波のはずですが、それを照射することにより、価電 子帯から伝導体への電子励起は、起きていないと思っております。X線回折実験で結晶構造解析する際には、電子励起が起きてい る状態の電子密度分布を測定していると思っておりません。しかし、X線の照射により電子励起が起きない理由がわかりません。
基本的なことばかりお聞きして、お恥ずかしいですが、きちんと理解しておきたいので、宜しくお願いいたします。
--------------------------------------------------------------------------------------------------------------------
Date: Fri, 15 Jun 2018 18:16:41 +0900
A: F様、佐藤勝昭です。 メールありがとうございます。
・X線と赤外ー可視ー紫外光とのちがいについてのご質問ですが、本質的な違いはありません。
電磁波の吸収は、散乱ではなく、基底状態<g|の電子が励起状態<e|に遷移することで起きます。
その遷移確率は、電気双極子遷移の場合、双極子モーメントをqrとして
|<g|er|e>|2
に比例します。
<g|→<e|のバンド間遷移による吸収係数α(ω)は、 α(ω)=(πωb2/2nc∫d3k fge δ(ω-ωge) (1)
ここに、fge は基底状態と励起状態の間の光学遷移の振動子強度であり、遷移確率に比例します。
fge=(2m/ℏ2)ℏωge |<e|qr|g>|2 (2)
振動子強度fgeがωに対して緩やかに変化する場合、吸収強度は結合状態密度Jgeと振動子強度の積で表されます。
α(ω)∝Jge・fge (3)
状態密度とは同じエネルギー間隔のなかにどれくらいの状態が存在するかですが、連結状態密度は、
Jge=∫∫dSdk = ∫∫dSdω/∇k(ωe-ωg) (4)
で表され、基底状態と励起状態がk空間(電子の運動量の空間)でのエネルギー分散曲線が平行のとき高くなります。
(山田・佐藤他「機能材料のための量子工学」(講談社1995, 第4章参照)
・可視光付近の光吸収は、価電子帯と伝導帯の間の遷移で決まりますが、連結状態密度は、van Hove 特異点付近で高く、 半導体では反射スペクトルのピーク付近で、吸収端より2-3eV高いエネルギーのところです。(Siでは吸収端は1.1eV, 反射のピークは3.5~4.5eV)
従って吸収端より波長が短くなるほど吸収が増えます。しかしもっと短波長になると、価電子帯ー伝導帯の間の バンド間遷移による吸収は、遷移確率の減少と、状態密度の現象によって弱くなります。
なお、質問(1)の「物質のバンドギャップエネルギーを超えない範囲内」では、光は透過するので波長依存性はありません。
・光子のエネルギーがずっと高くなって、keVのオーダーになると、バンドではなく、内殻に局在した電子が伝導帯に遷移する吸収が強くなります。
例えば、1s内殻からフェルミ準位以上の空いた状態への遷移はK吸収端と呼ばれ、2p内殻からの遷移はL吸収端と呼ばれます。
内殻電子状態の状態密度が高いので吸収は非常に強いのですが、吸収スペクトルの幅が狭く、これよりX線が短波長(高エネルギー)になると吸収は 起きません。つまり、吸収端を除けば、物質はX線に対して透明になります。 これによって、レントゲン写真が撮れるのです。骨に含まれるCaの内殻遷移が あるため、骨の部分が露光されず白くうつります。
・質問(2)のX線の侵入長ですが、短波長ほど侵入長が深くなるのは、エネルギーが高く、物質との相互作用が少なくなるため、吸収も散乱も受けないためと考えてよいでしょう。
・質問(3)の「X線の照射による電子励起が起きない」というのは間違いです。内殻から、フェルミ準位より上の空いた準位に電子励起が起きます。 --------------------------------------------------------------------------------------------------------------------
Date: Sun, 17 Jun 2018 16:13:44
AA: 佐藤先生
早速のお返事をありがとうございました。
教えて頂きましたことを調べながら考えたところ、点と点が線で繋がりました。
今後は、時間が空き次第、誘電率(実数部、虚数部)と光の屈折、反射、吸収、遷移の関係について、勉強して行きたく思っております。
化学科のため、このような話は授業ではやったことがないため、わからないことがありました時には、またお世話になるかもしれませんが、今後とも、どうぞ宜しくお願いいたします。
--------------------------------------------------------------------------------------------------------------------
1384.垂直反射の位相の式
Date: Sun, 8 Jul 2018 01:16:19 +0000Q: 佐藤先生;
メイルにて失礼致します。産業技術総合研究所の福田と申します。
いつも先生のHP、有り難く参照させて頂いております。
さて、垂直入射条件における光の反射をご説明下さっている項に関してご教示頂きたくメイル差し上げました。
e-Book「基礎から学ぶ光物性(工事中)第3章」 の (3.19)式、(3.20)式および 『光』の制御技術とその応用事例集第4章1節「光の反射メカニズム」ゲラ の(36)式 で位相飛びに関する関係式が示されていますが、これらの説明の本文の前半では、複素屈折率を n+ik と記載されているので、θ=Arctan(-2k/(n^2+k^2-1)) の 箇所は符号が逆(正しくは、θ=Arctan(2k/(n^2+k^2-1)))ではないかと言う気が致しましたが、その点ご教示頂ければ幸甚です。
瑣末な質問で恐縮ですが、よろしくお願い致します。
---------------------------------------------------------------------------------------------------------------------
Date: Sun, 8 Jul 2018 23:00:11 +0900
A: 福田隆史様、佐藤勝昭です。
再計算してみました。
r={(n^2+k^2-1)+2ik]/{(1+n)^2+k^2}
となり、福田様のご指摘通り
θ=tan^-1{2k/(n^2+k^2-1)}
となりました。
ご指摘ありがとうございました。ご指摘の箇所修正しました。
--------------------------------------------------------------------------------------------------------------------
1385.二色性偏光子についての質問
Date: Sat, 28 Jul 2018 08:49:36 +0900Q1: 佐藤勝昭 様, 初めまして。
私はR大3年のK*と申します。材料工学科に所属しております。 液晶や非線形光学現象について調べていたところ分からない部分がある中、こちらのホームページを拝見し質問の機会を頂こうと思った次第です。 お忙しい中恐縮ではございますが、以下の二点についてご教授して頂けたら幸いです。
①
「偏光アートでしおりを作ろう! 」のサイトでは、偏光とは 配向したヨウ素分子の方向によって光の透過or吸収(遮光)が決まると書いてありました。これは、伸びた長軸方向のヨウ素分子が、 同じ方向で振動をしている入射光によって揺らされることに光エネルギーを消費される=遮光されるからという解釈かと思います。
もしそうだとすればラマン散乱のように入射光を一旦吸収して、吸収した光の一部を再放出したりはしないのでしょうか。
光を再放出をしていたら光をカットしていないので偏光が出来ていないことになりますが、吸収された光エネルギーは分子の伸縮振動 の熱エネルギーにでも変換されたのでしょうか。
②
光の吸収というと半導体のバンド理論のように、材料のバンドギャップと入射光のエネルギーとの相性によって吸収の有無が関わってくるように 思えるのですが、波長の長さによって偏光しづらいなどといった偏光の波長依存性はありますか?
もし可視光線よりもずっと波長の長い赤外光領域やずっと波長の短い紫外光領域を確実に偏光するには、偏光材料をそれぞれどのような 工夫をすれば可能なのでしょうか。
まだ浅学のため的外れな考えや基礎的な内容かもしれませんが、何卒よろしくお願い致します。
---------------------------------------------------------------------------------------------------------------------
Date: Sat, 28 Jul 2018 23:31:28 +0900
A1: K君、佐藤勝昭です。
材料科学3年生なのによく勉強していますね。
質問にお答えしますが、わからなかったらまた質問してください。
①二色性偏光子についての質問
「これは、伸びた長軸方向のヨウ素分子が、同じ方向で振動をしている入射光によって 揺らされることに光エネルギーを消費される」という解釈ですが、「揺らされる」のでは ありません。一般に色素の光吸収は、色素分子の分子軌道の基底状態から励起状態への 電子遷移(電気双極子遷移)によって起きます。このとき、電子遷移の選択則によって、 偏光依存性が起きるのです。これは、分子の対称性(点群)に関係します。
(基礎から学ぶ光物性第8章 参照)

 さて、分子が光を吸収してその電子が励起状態になっていた場合、いつかは緩和して
基底状態に戻ります。戻る過程には、発光過程と、非発光過程があります。発光過程
でも、フォノン(分子振動)を伴いながら励起状態の底に移り、そこから基底状態に
もとより低いエネルギー(波長の長い)の光を放出して遷移する過程があります。
これをストークスシフトです。(左図参照)
さて、分子が光を吸収してその電子が励起状態になっていた場合、いつかは緩和して
基底状態に戻ります。戻る過程には、発光過程と、非発光過程があります。発光過程
でも、フォノン(分子振動)を伴いながら励起状態の底に移り、そこから基底状態に
もとより低いエネルギー(波長の長い)の光を放出して遷移する過程があります。
これをストークスシフトです。(左図参照)非発光過程では、右図に示すようにエネルギーの全てが分子振動になり熱になり、光は出しません。 (基礎から学ぶ光物性第9章 参照)
②偏光吸収の波長依存性
分子の場合、半導体の価電子帯に対応するのがHOMO(最も高い占有された分子軌道)、 伝導帯に対応するのがLUMO(最も低い非占有分子軌道)です。
この偏光依存性は①に書いたように光学遷移の選択則によります。HONO-LUMOギャップは、分子設計によって変えることが出来ます。
私のWeb資料「基礎から学ぶ光物性」を自習してください。
----------------------------------------------------------------------------------------------------------------------
Date: Wed, 1 Aug 2018 00:15:30 +0900
Q2: 佐藤勝昭 様
せっかく迅速な回答を頂いたのに、こちらからの返信が遅くなってしまい大変失礼致しました。
申し訳ないのですが、未熟者であるため疑問から更に疑問が生まれてしまいました。
★①配位座標モデルと励起状態の放物線について
添付された図(a)のように基底状態から励起状態に遷移するとき、急に右上に現れた別の曲線について確認したいです。
「電子は光に敏感で瞬間的に高いエネルギー状態に移れ、この変化に格子の動きは反応できない。だから光を吸収して 基底状態の曲線の極小点から同じ曲線の斜め上の高い点へずるずると登って行く=励起状態という考えはしない。 逆に、レナード・ジョーンズポテンシャルで考える熱膨張のように、エネルギーが高くなる際は時間を掛けながら格子の変形 を伴うときは同じ曲線で高い点へ登って行くという考えをする」という解釈でよろしいですか?
以上の仮定(解釈)をも とに、熱膨張と同様に光励起によっても格子間隔はr1からr2へと広がるという意味なんでしょうか? 横軸の配位座標というのが具体的に何なのか分からないのと、図によっては横軸が波数kで似たような図が描かれているの で余計に混乱しております…。
★②偏光は偏光板の向きと振動電場の向きが関わるのではないか
材料本来のバンド構造で吸収する光が決まりますが、これには振動の方向という情報は含まれておらず、特定の波長の 光なら振動方向によらず全て吸収するように思えます。
それだと前回添付したサイトにあるように、偏光板を回転させてみても明るさは変化しないのではないでしょうか。
佐藤先生から頂いたスライド資料には、光学遷移の選 択則について分子軌道や化学結合の話は載っていたのですが、 偏光板の角度と振動電場の角度の関係によって吸収する/しないが異なる理由について分かりませんでした。
例えば延伸処理をして分子間距離を変えることでバンド構造が変化し、特定の波長の光を吸収しやすくしているのですか?
(もし載っているのに見逃していたり、ただの理解不足でしたらすみません。)
★③ 偏光板が光吸収に必要な要素
仮に赤外光を偏光板で遮蔽する場合、材料のHOMO-LUMOギャップが赤外光のエネルギーと同程度にすれば良いという 理解でよろしいでしょうか?
その場合、波長が長い光だと偏光膜をそのまま透過されやすい気がするのですが、単純に材料選びだけでなく膜厚を厚く した方が良い等その他の重要な工夫がありますか?
質問事項が多く、長文失礼いたしました。お時間のある時にでも付き合っていただければ幸甚です。
----------------------------------------------------------------------------------------------------------------------------
Date: Wed, 1 Aug 2018 01:27:48 +0900
A2: K君、佐藤勝昭です。
 ★①配位座標モデルと励起状態の放物線について
★①配位座標モデルと励起状態の放物線について基礎から学ぶ光物性第9章の6.ストークスシフト にありますように、電子のエネルギー状態は、電子を束縛している 原子の位置に依存しています。基底状態のエネルギーはr1を中心に 放物線を描いています。一方励起状態の電子のエネルギーはr2を中心 に放物線を描きます。
基底状態の極小位置にある電子が光を吸収して励起状態に移るとき、 電子の遷移は原子核の運動に比べて短時間に生じ、図 (a) の 1→1‘ のように垂直遷移します。1 ’は励起状態としては不安定な状態なので フォノンを放出しながら励起状態の最低エネルギー位置r2に移ります。
格子間隔が変わるのではなく、励起状態の電子の位置が基底状態の位置 からずれているのです。(これはピコ秒のレーザーを使って確かめられ ています。)この緩和時間 は10-12~10^-10 s(1~100 ピコ秒)です。
? 励起状態から基底状態への遷移も 2→2‘のように 垂直に起き、 そのエネルギー差を光として放出します。基底状態の2 ’状態も不安定 なので、再びフォノン(熱)を放出して1にもどります。
? このように励起後緩和過程で 光の エネルギー一部が熱として失われ るため発光のエネルギーは励起エネルギーより小さくなります。
「高い点へずるずると登って行く」ということはありません。
★k空間のバンド分散曲線と似ていますが、配位座標はあくまで実空間 の座標です。
★②偏光は偏光板の向きと振動電場の向きが関わるのではないか
「材料本来のバンド構造で吸収する光が決まりますが、これには振動の 方向という情報は含まれておらず、」は間違いです。例えばLEDに使われる 窒化ガリウムGaNは六方晶で、電場ベクトルがc軸に平行な偏光と、垂直な 偏光では、選択則が違うのでスペクトルが変わります。
基底状態の波動関数φ1、励起状態の波動関数φ2とします。電気双極子 遷移の遷移確率は|∫φ1*(qx)φ2dτ|2によって表されますが、対称性 によって選択則が変わるのです。
電気双極子qxはx方向の電場振動で誘起されます。これが偏光と関係づる 選択則をもたらします。選択則を群論で理解するには、ランダウリフシッツ の量子力学の教科書がわかりやすいですよ。
★③ 偏光板が光吸収に必要な要素
二色性偏光子は、吸収帯がなければ起きません。HOMO-LUMOギャップを 工夫するしかないでしょう。
複屈折を用いれば波長選択制のない偏光子ができます。
グラントムソン偏光子は方解石の複屈折を使っています。
--------------------------------------------------------------------------------------------------------------------------------
Date: Thu, 2 Aug 2018 06:29:15 +0900
AA: 佐藤勝昭 様
度々のご返答ありがとうございます。
大変勉強になりました。
お忙しいところ誠に有難うございました。
--------------------------------------------------------------------------------------------------------------------------------
Date: Sat, 2 Mar 2019 23:06:52 +0900
1386.強磁性体の透磁率について
Q1: 佐藤勝昭 様初めまして。
私はH*大学に所属しております2年生のU*という者です。
磁性体に興味があり、コツコツ参考書を読んでいるのですが、私には難解でなかなか理解できない点が多くあります。
またお手数ですが、学校名、氏名は匿名にてよろしくお願いいたします。
①まず基本的な事ですが、鉄などの強磁性体は透磁率が高いですが、透磁率が高いとは周囲の磁束を磁性体内に集めやすいという意味なのでしょうか?つまり、磁束は空気中よりも鉄の方が通りやすい為、周囲に存在する楕円形状の磁束のループの形を歪めて磁性体の方へ向かうから磁束密度としても高くなるのですか?
①' 変動磁場が鉄板を貫くと渦電流が流れます。これは鉄板を貫く磁束の変化を妨げるように働くためだと思いますが、磁場の侵入を妨げるのならむしろ透磁率が低くなるように解釈してしまい矛盾しているように思います。また超伝導状態は磁束の侵入を遮蔽するので、透磁率がゼロという解釈になるのですか?
②磁性体はノイズとなる磁束をよく吸収してくれる磁気シールドとして使われると参考書に書いてありました。おそらく磁束を吸収→交流電流→発熱という過程であり、この場合は透磁率が高い方が適していると思います。しかし磁気シールドに交流の渦電流が流れると、その渦電流による磁場が出来てノイズとして返してしまうような気がするのですが、そのようなことはないのでしょうか。
よろしくお願い致します。
-------------------------------------------------------------------------------------------------------------------------------
Date: un, 3 Mar 2019 00:56:08 +0900
A1: U*君、佐藤勝昭です。
2年生なのによく勉強していますね。磁性体は、磁性体が本来持っている性質の他にバルクか、薄膜か、棒状かなど形状に依存したり、磁区や磁壁など実際の作製条件による マクロな性質もあるので簡単ではありません。この辺りのところは私の著書を参考にして下さい。「磁性工学超入門」(共立出版,2014)第3章の原稿pdfを添付します。
ご質問にお答えします。
(1)強磁性体の透磁率
磁束密度Bと磁界Hの間には、B=μ0 μr H の式が成り立ちますがこの比例定数μrが比透磁率です。これは磁束密度と磁界が比例する場合にのみ有効です。
強磁性体の内部では磁束密度Bは外部磁界Hと磁化Mの和B== μ0H +Mで表されます。磁性体内部の磁束密度は図3.4のように非常に高密度になっています。
従ってBをHで単純に割ると非常に大きな値になります。あなたはこれを「透磁率が高いとは周囲の磁束を磁性体内に集めやすい」と表現したのですね。
「磁束は空気中よりも鉄の方が通りやすい」というのではなく「鉄中に磁化Mがあるので磁束密度が高い」というのが正確な表現です。
しかし、磁化Mは添付の図3.16のように磁気ヒステリシスをもちMとHは比例しません。ただ、初磁化曲線(図3.18)のAB付近では、MはHに比例します。強磁性体の内部は 磁区に分かれていて、磁界を加えると磁壁(磁区の境目)が動きます。このときMはHにほぼ比例しますが、このときの透磁率(初透磁率)は磁壁移動のしやすさで 決まります。従って、強磁性体の透磁率は、単純な描像では描けません。
(1’)変動磁場と渦電流
鉄は金属です。このため、外部からの変動磁場に対して、この変動を抑えようと渦電流が流れます。このような性質を反磁性といいます。この場合透磁率は負の値を 持ちます。「透磁率が低くなるように解釈」してよいのです。渦電流を押さえるにはナノ粒子にして、電流のパスを切ったり、積層鉄板のように絶縁体を挟んで電流の パスを切ったりしています。フェライト磁石のような絶縁体を使えば渦電流はありません。
(2)磁気シールドに対する渦電流の影響
磁気シールドには、パーマロイのようなソフト磁性体を使います。磁束は透磁性の高い物質を通る経路をとるため、中に入り込まないのです。
交流の電磁波は表皮効果によって非常に薄い層の中で吸収され、奥に入りません。これは渦電流の効果です。外部磁界を打ち消す効果なので新たなノイズになりません。
ステルス戦闘機では、レーダーの電磁波を反射させないで吸収するために的から見えません。ここでは、強磁性共鳴を使います。磁気モーメントが共鳴して回転し吸収が起きます。
------------------------------------------------------------------------------------------------------------------------------
Date: Sun, 3 Mar 2019 16:23:57 +0900
Q2: 佐藤勝昭 様
ご回答だけでなく資料までいただき、有難うございます。
ただまだしっかりと理解しきれていない為、もう少しだけお付き合いお願い致します。
①資料の3.1.2章でも記述がありますが、なぜ強磁性体内部では磁束密度がB=μ0H+Mという和で表せるのですか?透磁率という概念が掴めていません。
強誘電体であれば電束密度D=P+εrEで、元々の自発分極Pの成分に加え、外部電場εrEによって正負のイオンを更に引き離して分極を大きくしているので和で表せるかと思います。(分極をバネの弾性エネルギーに例えれば、元々の変位分の弾性エネルギーに加えて外部電場で更にバネを伸ばしているのでエネルギーが大きくなるイメージです。)
一方、Mは自発磁化で磁気モーメントが元から揃いやすく安定した材料において現れる項で、仮にこのMが初期状態ではx軸から角度θの向きだったとします。この状態ではx軸方向の磁化(磁束密度)はB=Mcosθしか持っていません。ここでx軸方向に外部磁場Hを掛けた場合、磁化の向きを回転させてx軸に平行で揃うので、磁束密度はB=Mで大きくなる。これだと強誘電性のように更に外部磁場μ0H成分を単純に足していいの?と疑問に思えてしまい、B-M=μ0Hで、強磁性体が磁束密度が高いのは透磁率が高いからではなく元々大きい自発磁化のおかげと思えてしまいます。
②磁気シールドは表面の薄い層のみで電磁波が吸収されて渦電流に変わるが、外部磁場を打ち消す方向に流れているので、渦電流によって発生した磁場と外部磁場がキャンセルされるって認識で合っていますか? またフェライトのような絶縁体であれば渦電流は抑制できるとの事ですが、この場合は磁場→渦電流→熱というエネルギーの変換ではなく、磁場→強磁性共鳴→熱という変換ですか?
-------------------------------------------------------------------------------------------------------------------------------
Date: Sun, 3 Mar 2019 23:55:19 +0900
A2: U君、佐藤勝昭です。
(1)強誘電体との比較
磁性体のB=μoH+M と誘電体のD=ε0E+Pは全く同じです。
P=ε0χEとすればD=ε0(1+χ)Eとなり、1+χ=εrなのです。
強誘電体では自発分極があるため、PとEの間には比例関係がありません.
強誘電体では分域(磁区に相当)があり、分域壁の移動がおきている点も強磁性体と同じです。
実は、強磁性ferromagnetism)の方が先に見出されていて,これのアナロジーで強誘電性をferroelectricityというのですよ。
ferroは鉄のという接頭辞です。
(2)磁気シールド
あなたの解釈でよいと思います。
-------------------------------------------------------------------------------------------------------------------------------
Date: Tue, 5 Mar 2019 03:33:38 +0900
AA: 佐藤勝昭 様
大変お忙しいにもかかわらず、多くの事を教えて頂きありがとうございました。
-------------------------------------------------------------------------------------------------------------------------------
Date Wed, 17 Apr 2019 16:12:20 +0900
1387.金属の反射について
Q1: 佐藤勝昭 先生、はじめまして、W*大学3年のM*といいます。佐藤先生のHPを拝見させてもらいました。お手数ではありますが質問に答えていただけるとありがたいです。
一般的に金属に電磁波を照射したとき、プラズマ振動数以下の電波・赤外光・可視光の電磁波を反射する金属光沢の性質を持っています。
例えばAuに自然光を照射した場合、赤色と黄色に相当するスペクトルの光をよく反射するから、私たちの目には金色とされる色に見えていると思います。 しかし、その一方で反射されなかった緑色や青色の波長の光エネルギーはどこへ行くのでしょうか?
上記は金属に何も負荷を掛けていない時の話ですが、もし直流電流を流している金属配線に光を照射すると、電流としての電子の流れとプラズマ振動 が重なり複雑になって反射率が変化しますか?さらに電気特性の観点から見れば、電子の運動が乱されるので電流量の減少=電気抵抗の増加に寄与する のですか?入射光の強度や偏光状態を選べば、電流量を調整できるのかなと疑問に思いました。
また、もし金属配線に赤色の光に相当するTHzレベルの高い周波数の交流電流を流した場合、電流自体がプラズマ振動とほぼ同様の振舞いになって 赤色の光を放出するようになるのでしょうか。
回答をよろしくお願い致します。
---------------------------------------------------------------------------------------------------------------------------------
Date Thu, 18 Apr 2019 10:11:28 +0900
A1: M君、佐藤勝昭です。
金属の反射について、次のスライドを参考にして勉強して下さい。
「物質と光の相互作用―金属の誘電率と電子分極の電子論」
 (Q1) 反射されなかった緑色や青色の波長の光エネルギーはどこへ行くか?
(Q1) 反射されなかった緑色や青色の波長の光エネルギーはどこへ行くか?(A1) 添付図の反射スペクトルを見て下さい。赤も黄色も100%反射するわけではありませんし、 青も緑も反射されないわけではなく40%くらいは反射しています。
金の反射率が2.2eV付近で急落するのは純粋の自由電子プラズマではなく、スライドの22枚目 「3.バンド間遷移と束縛電子モデル]にありますように、満ちたd電子バンドからフェルミ準位 以上の空いたバンドへのバンド間遷移による吸収が始まるためです。そのため26枚目のスライド 「3.2 自由電子プラズマ振動とバンド間遷移のハイブリッド」の誘電率のスペクトルのように 損失を表す誘電率の虚数部は、実数部がゼロに近づくあたり(遮蔽されたプラズマ周波数)で ピークになっています。この周波数以下では、誘電率の実数部が負なので、中に電磁波が入り づらくて高い反射率になっており、この周波数以上では、吸収が起きてそのエネルギーは熱に なります。
(Q2)直流電流を流して反射率は変化するか
(A2)上の問題にあるように金の反射率の急落を決めているのは、バンド間遷移という物質固有の ものなので、金属内の自由電子の流れによって大きく変化することはありません。
(Q3)光照射によって電流量は制御できるか
(A3)半導体に光を当てたときは、もともとキャリアが少ないので、光学遷移による吸収で電流が 変化する現象(光伝導)がありますが、金属では、キャリア数が多いので光照射による変化は ありません。
(Q4)金属に赤色の光に相当するTHzレベルの高い周波数の交流電流を流した場合、電流自体が プラズマ振動とほぼ同様の振舞いになって赤色の光を放出するか?
(A4)可視光の赤は波長約600nmです。振動数は3x10^8/600x10^-9=5x10^14Hzで、THz光の500倍の 周波数です。質問自体がナンセンスです。赤い光が放出することはありません。
-----------------------------------------------------------------------------------------------------------------------------------
Date: Fri, 19 Apr 2019 08:33:47 +0900
Q2: 佐藤勝昭 先生、Mです。回答有難うございます。
(Q4)についてですが質問の仕方が悪くてすみませんでした。
赤色の光に相当する周波数の交流電場を掛けると配線が赤色に発光し、青色の光に相当する周波数の交流電場を掛けると配線が青色に発光するのかという意味でした。
可視光領域ではなくても赤外光に相当する交流であれば、配線からは目に見えない赤外光の電磁波を出すのでしょうか。
ご回答よろしくお願い致します。
-----------------------------------------------------------------------------------------------------------------------------------
Date:Fri, 19 Apr 2019 09:32:07 +0900
A2: M君、佐藤勝昭です。
赤色の光に相当する周波数の交流電場は光の周波数なので電流として加えることはできません。
赤色の周波数の電磁場を受けると、金属の中では電子が電場の+方向に動き電場と反対極性の電気双極子を作ります。
この状態は誘電率で表すと実数部が負の値をとる状態です。誘電率の実数部は,屈折率nと消光係数κを使って
ε'=n2-κ2
と書けますが、これが負の値をとるというのはn<<κ、すなわち消光係数(光吸収に相当)が非常に大きい状態です。
強い吸収が起きているのです。従って、赤い光によって電気双極子が生じ、この電気双極子がただちに光を発しているために、 強い反射が起きていると解釈することができます。
◆目に見えない赤外線では、もっと強くこのことが起きています。
◆青色の場合は、誘電率は負ではなく、単純に吸収がおきます。吸収されたエネルギーはただちに熱になるので、発光は起きません。
-----------------------------------------------------------------------------------------------------------------------------------
Date:Sun, 21 Apr 2019 13:27:40 +0900
Q3: 佐藤勝昭 先生、Mです。再びご回答有難うございます。
赤色光のような波長の長い光は金属表面でほぼ反射してしまう=金属表面で光吸収→再放出=金属内部へ侵入しない=消光係数κが大きい=ε'が負
青色光のような波長の短い光は金属表面で反射する量が少ない=金属内部へ侵入していく=消光係数κが小さい=ε'が正
ということで合っていますか?
>赤色の光に相当する周波数の交流電場は光の周波数なので電流として加えることはできません
おっしゃる通りなので、おそらくご回答では可視光や赤外光を外から照射した場合を説明していただいたのかと思いますが、 配線にマイクロ波のような周波数の低い交流電場を直接印加したときは配線の周囲にマイクロ波を放射するのでしょうか?
何度もすみませんが、ご回答よろしくお願い致します。 ------------------------------------------------------------------------------------------------------------------------------------
Date: Mon, 22 Apr 2019 13:58:27 +0900
A3: M君、佐藤勝昭です。
前半の解釈はよいと思います。
後半ですが、マイクロ波は、スマホにも使われる周波数です。同軸ケーブルのような伝送線路に高周波を加えた場合、 インピーダンスマッチングが悪いとエネルギーが線路に伝わらず反射します。
マッチングが取れれば、線路を伝わって負荷にエネルギーが伝わります。もしその時にあなたの言うようなことが起きたら、 電力は放射して失われます。
したがって、インピーダンスマッチングが取れていれば放射は起きず、取れていなければそもそも線路に入っていかないと解釈できます。
------------------------------------------------------------------------------------------------------------------------------------
Date: Tue, 23 Apr 2019 20:57:39 +0900
AA: Mです。
おかげさまで光物性について理解を深めることが出来たかと思います。
何回も私の質問に付き合っていただき有難うございました。
------------------------------------------------------------------------------------------------------------------------------------
1388.クロム鋼の磁化について
Date: Thu, 25 Jul 2019 21:16:06 -0400Q1: 初めまして!
部品メーカーで金属加工を実施しております水谷と申します.
突然で申し訳ありませんが,HPを閲覧致しまして,私も金属の磁化について質問させて頂きたいと思った次第です.
弊社ではSCr440の製品を切削加工しておりますが、ある日突然,切削後に製品に磁気が帯び始めました.
(製品に切粉が付着したり,一部の測定具が製品にくっついた為気付きました)
色々調べた結果,材料の問題ではないかと推測するに至りました.
理由としては,設備・測定具は特に磁化されていない.
変化点として,製品に磁気を帯び始めたと同タイミングで材料メーカーが磁粉探傷を始めたからです.
ただし,材料メーカーでは磁粉探傷後に当然ながら脱磁工程もあり,脱磁後に粗材の表面をテスラメータで測定すると 0~0.3mT程度であり,しっかり脱磁されています.
しかしながら,弊社で切削すると高いものでは,8.0mTもの磁性を帯びてしまいます.
材料の段階では磁気がないのに,材料を削れば削るほど磁気が現れるのです.
(径を細く削るにつれて,磁気が高くなる印象です)
金属材料を切削すると磁気を帯びるのは分かるのですが,材料メーカーが磁粉探傷を始める前の製品では,切削後でも0.5mT程度であり 磁粉探傷が要因なのは明らかなのですが,
磁気抜きされた材料なのに,加工で磁気が極端に入るという現象が不可思議でたまりません.
磁気抜きが不十分で,材料内部に磁気が残っている?なんていう事がありますか?
それとも一度磁化されたせいで,磁気抜きしたとしても磁化しやすい材料になってしまうのでしょうか.
どういった現象が起きてこうなっているのか,アドバイス頂けると助かるのですが.よろしくお願い致します.
................................................................................
Date: Sat, 27 Jul 2019 09:42:33 +0900
A1: 水谷様、佐藤勝昭です。
むずかしい質問です。
「磁粉探傷」によって、「クロム鋼の磁性が変化して、切削による磁化が強くなったのではないか」という質問ですね。
JIS G 0565-1992によれば、「磁粉探傷」の際の磁化方法として次の7つが規定されています。
それぞれの磁化処理によって、磁区構造に変化が起きます。
脱磁とは、磁区の磁化方向をランダムにして、マクロの磁化をゼロにしているのですが、 切削加工による応力磁壁移動が起き、磁壁がピン止めされるために磁化が生じます。
磁区構造が磁粉探索の際の磁化処理によって変化しているので、磁壁のピン止めも変わるのではないでしょうか。
材料メーカーに、どのような磁化処理をしたか問い合わせてみてはいかがですか?
----------------------------------------------------------------------------
Date: Wed, 31 Jul 2019 23:41:06 -0400
Q2: 佐藤様
ご丁寧な返信ありがとうございます.
材料メーカーに問い合わせたところ,軸通電法でした.
弊社も同じ軸通電法の磁粉探傷機を持っていますので、材料メーカーが磁粉探傷を実施していない材料で 弊社で磁粉探傷⇒脱磁⇒切削してどうなるかトライしてみました。
結果としては,磁化の程度は弱いものの,通常より磁化しました(磁粉探傷なし 0.2mT ⇔ あり 1.5mT).
以上から,「磁粉探傷」によって、クロム鋼の磁性が変化して、切削による磁化が強くなった。 と,言えるのかなとは思います.
>磁区構造が磁粉探傷の際の磁化処理によって変化しているので、磁壁のピン止めも変わったのでは?
⇒ 磁化が強くなるということは,磁壁の移動を妨げる障害が増えて,
ピン止めが発生する箇所が増えたというイメージでしょうか.
現実問題,切削による磁化がこんなに増えてもらっては困るのですが,
(通常 金属部品の磁気残りの図面規格は0.5mT以下であり,不良になる為
切削後の完成品で弊社が磁気抜き工程を追加する事態になっています。。)
切削による磁化をなくすには,磁粉探傷をやめるしか手はありませんか?
何かアイディアがあれば,助かります。
--------------------------------------------------------------------------------
Date: Thu, 1 Aug 2019 15:59:39 +0900
A2: 水谷様、佐藤勝昭です。 軸通電法ですか。この場合電流による磁束は円周方向なので、磁化も円周方向に起きます。
円周方向の磁壁が試料表面付近でのピン止めされている可能性が無いとは言えません。
脱磁は、円周方向の磁化をランダムにしなければならないので、交流の通電で電流値を 徐々に下げていくような脱磁が必要ではないでしょうか?
---------------------------------------------------------------------------------
1389.亜鉛ウィスカについて
Date: Tue, 19 Nov 2019 10:40:05 +0000Q1: 佐藤先生、K*社のB*と申します。HPを見て、問い合わせをさせていただきました。
お手数ですが、下記ご回答いただければ幸いです。
SUS304に下地Niめっき+電気亜鉛めっき+黒クロメートをしたもので、 ウィスカが発生する事例があり、成分分析したところ、亜鉛ウィスカと判明しました。
亜鉛めっきはウィスカが発生し得るものと理解していますが、一方で、鋼板への亜鉛めっき 等はごく一般的であります。
では、どのような場合に発生しやすいのか? どのような場合に注意すべきか?など、 ポイントが理解できていません。
そこでご相談ですが、被着体の材質や、めっき工法(電解or溶融めっき)など、亜鉛ウィスカが 発生しやすい組み合わせ等に関して、ご知見をお持ちでしたら、ご教示いただけないでしょうか。
※ 文献を調べる限り、溶融めっきだと熱処理による残留応力の緩和効果で発生しにくいという 情報が得られましたが、実用的には電解メッキを採用することが多く、できれば溶融めっきは 採用したくないと考えています。
以上、ご確認よろしくお願いします。
----------------------------------------------------------------------------------
Date: Wed, 20 Nov 2019 08:04:00
A1: B様、佐藤勝昭です。
亜鉛ウィスカは、電子産業で1950年代からの問題でした。
1954年にFisherらが圧縮歪みの勾配がウィスカ成長の原因と述べました。
1976年から1980年代にかけ、Lindborgらがウィスカがマクロなストレスが45N/mm3以下であれば 成長しないこと、有機物が関与するとウィスカが生じやすいことを明らかにしています。
最近では、電顕による観察が進みましたが、防止方法については十分な発展がないようです。
添付のLiang Wuのレビューをお読み下さい。
-----------------------------------------------------------------------------------
Date: Wed, 20 Nov 2019 10:09:02
Q2: 佐藤先生、早速のご確認ありがとうございます。いただいた資料ふくめ、もう少し調べてみました。
光沢剤などメッキ添加剤によって、内部応力が残留することがあるようですね。
またそもそもですが、実用上、ウィスカを気にすべき金属は、スズと亜鉛のみと考えて問題ないでしょうか?
(この2つは、再結晶温度が常温付近と低いため、ウィスカ発生の可能性あり、と理解しています)
以上、よろしくお願いします。
-----------------------------------------------------------------------------------
Date: Thu, 21 Nov 2019 19:51:38
A2: B様、佐藤勝昭です。
スズと亜鉛はおっしゃるとおり低温で再結晶化するのでほとんどのレポートはこの2つに集中しています。
ただ、わたしが経験したことではAg2S(硫化銀)のウィスカがあります。
調べてみると、富士通のサイトに硫化銀の写真が出ていました。
-----------------------------------------------------------------------------------
Date: Fri, 22 Nov 2019 00:12:39
AA: 佐藤先生、硫化銀のウィスカ、初めて聞きました。ありがとうございます。
亜鉛ウィスカに関して、我々の方でも、もう少し調べてみます。
今回迅速に情報、知見をいただきまして大変助かりました。
また別の機会で相談させていただければ幸甚です。ありがとうございました。
それでは失礼致します。
-----------------------------------------------------------------------------------
1390.黒鉛(グラファイト)の加工粉について
Date: Fri, 7 Feb 2020 05:40:49 +0000Q: 佐藤勝昭様 K*社のE*と申します。匿名でお願いします。
HPを以前から拝見させていただき初めて質問させていただきます。
黒鉛を機械加工で加工したときやサンドペーパーで研磨したとき、加工粉が表面に物理的 に付着して鏡面のよう光沢ができる場合とできない場合があります。
アルコールを浸した布で拭うと表面の粉が除去されてと光沢がなくなりますが、超音波洗浄 だけでは完全に除去できないような付着力です。
質問ですが、 1、光沢ができるのは、もともと存在した黒鉛の表面の凹凸に加工粉が押し付けられて 平滑になっただけで見えるのか、または、押し付けられて付着した黒鉛の結晶構造がそろい ながら表面層が形成されているのでしょうか。
2、黒鉛を加工して出てきた粉末は、元の素材と黒鉛の結晶度も同じなので異なる炭素 材料よりも圧粉すると、結合というか付着しやすいと考えられるのでしょうか。
お忙しいなか恐縮ですがお答えをいただければと存じます。
-----------------------------------------------------------------------------------
Date: Mon, 10 Feb 2020 10:30:02
A: E様、佐藤勝昭です。 メールありがとうございます。私はナノカーボンは専門でないので専門家に相談し、 つぎのように回答します。
(1)の光沢について
グラファイトは、炭素が蜂の巣状に結合した2次元のグラフェンのシートがその面に垂直の 方向(c軸方向)にファンデアワールス結合した結晶です。グラフェンシートの面内の電子 移動度は高く、金属と同様の伝導性を示しますが、電子密度が低くドルーデの自由電子による 反射率は高くありませんが、加工でファセット(結晶面)がでていると平坦なので、いわゆる 黒光りになります。
グラフェンに何らかの方法でドーピングすると、電子密度が増加し金属光沢をもちます。 例えば、リチウムを添加すると、金ぴかになることが報告されています。
しかし、グラフェン一層では反射率が高くないので、多層グラフェン、すなわちc軸方向に 配向性の高い高配向性熱分解グラファイト(HOPG)に近い状態になっているのではないでしょうか。
(2)の付着力について
グラフェンシートは原子レベルの平坦性をもつので、ファンデアワールス結合が強く働くため、 はがれにくいのだと考えられます。
------------------------------------------------------------------------------------
Date: Tue, 11 Feb 2020 22:19:13 +0000
AA: 佐藤勝昭様
早々に回答いただきありがとうございました。
サイトはかなり昔から知っていましたが、知識の浅い質問にも 分かりやすくご教示下さり、他の質問とご回答も非常に参考に なります。また、新たに疑問がでましたら是非質問させていた だきたいと思います。よろしくお願いいたします。
------------------------------------------------------------------------------------
1391.電気化学発光(ECL)の局所表面プラズモン共鳴(LSPR)による増強
Date: Wed, 13 May 2020 11:09:52Q1: 佐藤勝昭様
C*大学M1のF*と申します。HPを拝見し、メールさせていただきました。
現在、私は電気化学発光(ECL)とLSPRとの相互作用を研究しています。
論文などを閲覧していると、金属ナノ粒子のLSPRによる蛍光体の蛍光が増強する金属増強蛍光(MEF)なる現象が多く報告されています。しかしこの現象のメカニズムがよくわかりません。
1.LSPRによる蛍光体への影響
2.プラズモン吸収と発光体の吸収や発光スペクトルがオーバーラップしていることが最適条件と書いてあるが、なぜかよくわからない。
3.MEFはフォトルミネッセンス(PL)によるものが多く方向されているが、ECLでもその現象を発現可能なのか(理論的に)。
使用している材料
金属ナノ粒子:金(30 nm)
蛍光体:ルテニウム錯体(励起波長455 nm、発光波長:610 nm)
お忙しいと思いますが、回答よろしくお願いします。
また本質問は匿名で匿名扱いでお願いします。
-------------------------------------------------------------------------------------
Date: Wed, 13 May 2020 14:45:16
A1: F君、佐藤勝昭です。
プラズモンについては、私の解説「プラズモンの基礎」を読んでください。
学振147委員会第118回研究会「プラズモンが拓く機能と応用」(主婦会館)2012.12.07
スライド
予稿
補足資料
その上で3つの質問に簡単にお答えします。
- LSPRによる蛍光体への影響
 蛍光体からの光の電界が局在プラズモン共鳴を受けて増強されます。
蛍光体からの光の電界が局在プラズモン共鳴を受けて増強されます。
スライドの51枚目、52枚目をご覧下さい。
球状の金属粒子の場合ε(ω)+2が0のときに局在プラズモン共鳴が起きます。
金の場合ε(ω)が-2になるのは添付図に示すように2.5eV付近(~500nm青緑)で起きます。
- プラズモン吸収と発光体の吸収や発光スペクトルがオーバーラップしていることが最適条件と書いてあるが、なぜかよくわからない。
上に述べたように金の球状粒子の場合、電界の増強が起きるのは500nm付近(多少ブロードでしょうが)のみなのです。
- MEFはフォトルミネッセンス(PL)によるものが多く方向されているが、ECLでもその現象を発現可能なのか(理論的に)。
発光は、何らかの原因で励起状態になった電子系が基底状態に戻るときに、そのエネルギー差を光として放出する現象です。
蛍光は、波長の短い光によって電子を励起状態にします。電気化学発光では、電極上で発光材料の酸化反応と還元反応が生じ 衝突で電子授受反応が生じ励起状態を生成し、これが基底状態に戻るときにそのエネルギーを光として放出します。
(私はECLの専門家ではありませんので指導教員に確かめてください)
電子系の励起状態が基底状態に戻るときに発光するという点では、蛍光でも電気化学発光でも同じです。出てきた光の電界を プラズモン共鳴で増強するのです。
Date: Wed, 13 May 2020 15:53:54
Q2: 佐藤様、Fです。
早速の返信ありがとうございます。
最後の「出てきた光の電界をプラズモン共鳴で増強するのです」についてなのですが
○ PLによる増強
→励起光を照射した際、蛍光体の励起状態生成はもちろん、LSPR発現(励起光は吸収ピークではないが)も誘発する。
蛍光体が基底状態に戻る際に発した光をLSPRにより増強させる。
○ECLによる増強
→PLと違い励起光が存在しないECLでは、蛍光体が発した光によりLSPRを誘発し、このLSPRが蛍光体の発した光を増強する
という認識でよろしいですか?
また、金属ナノ粒子近傍に蛍光体が存在しているとき金属にエネルギーが移動するとは、これは金属のバンドギャップ遷移に使われたということですか?
-------------------------------------------------------------------------------------
Date: Wed, 13 May 2020 16:57:35
A2: F君、佐藤勝昭です。
○ PLによる増強:
確かに、励起光が共鳴で増強される場合も考えなければなりませんね。
○ECLによる増強
この場合は、発光した光の増強だけしかありません。
以上、あなたの認識で結構です。
「金属ナノ粒子近傍に蛍光体が存在しているとき金属にエネルギーが 移動するとは、これは金属のバンドギャップ遷移に使われたということですか?」
という質問ですが、
金属の誘電率の急激な変化はバンド間遷移が始まる光子エネルギーで起きる のですが、私の考えでは、この光子エネルギーで金属の自由電子プラズマ共鳴が 起きて、その緩和過程にはバンド間遷移の吸収が関わっているというのが正しい と思います。
---------------------------------------------------------------------------------------
Date: Thu, 14 May 2020 14:03:40
A2': 補足します。蛍光体と金ナノ粒子が接近しているときのエネルギーの移動ですが
蛍光体→光のエネルギー→金の自由電子系にプラズマ振動を励起
→金の4dバンドからフェルミ準位に電子を遷移させる
→最終的にフォノンを放出して緩和→熱エネルギーになる
と考えられます。
おわかりいただきましたか?
---------------------------------------------------------------------------------------
Date: Thu, 14 May 2020 14:23:20
AA: 佐藤勝昭様、Fです。
再度メールしていただきありがとうございます。物理範囲はまだまだ勉強不足で、返信遅れてしまいました。
エネルギー移動についての機構理解出来ました。
化学系の研究室なのでなかなか物理領域についての知見を得る機会がなく今回は大変貴重でした。
ありがとうございます。
----------------------------------------------------------------------------------------
1392.「光と磁気(改訂版)」p120 図6.3(a)の縦軸の目盛が原著論文の図と異なる
Date: Fri, 10 Jul 2020 04:40:13Q: 東京農工大学名誉教授 佐藤勝昭 様
はじめまして。Y*大学M2 H*と申します。ホームページを拝見させていただきました。
私は現在、Ce:YIGの磁気光学効果について研究しており、佐藤先生の『光と磁気〔改訂版〕』を教科書に勉強させていただいています。
教科書の中で気になる点が2つあったので匿名で質問させてください。
p120 図6.3(a)(b)についてです。
・引用元の論文p904を見ると、教科書と縦軸のスケールがあっていないようです。
・教科書の図と論文の図を重ねてみると、少しずれがあるようです。
論文にerrataがあり、修正されたのかと思い、探したのですが見つけることができませんでした。
気になったのでメールさせていただきました。
よろしくお願い致します。
----------------------------------------------------------------------------------------
Date: Fri, 10 Jul 2020 21:34:33
A: H様、佐藤勝昭です。
ご指摘の通りです。図6.3(a)のスケールは、私がトレースした時にミスをしたようです。
原論文の図をお使いください。
図8.3(b)のεxy"は論文のε1"と符号が反対です。これはεxyの定義のちがいによるものです。
ホームページでERRATAを出したいと存じます。
ご指摘ありがとうございました。
-----------------------------------------------------------------------------------------
Date: Fri, 10 Jul 2020 13:15:04
AA: 佐藤勝昭 様,Y大学大学院 Hです。
お忙しい中、返信ありがとうございました。
勉強を始めた当初は公開されているスライド等も参考にしていました。
大変勉強になりました。
重ねて感謝申し上げます。
------------------------------------------------------------------------------------------
1393.未アニールシリコンウェハーのPN反転、抵抗値について
Date: Fri, 27 Nov 2020 18:22:51 +0900Q1: 佐藤勝昭様
初めまして。F社のMと申します。HPを拝見し、初めて質問させていただきます。
掲載の際は匿名でよろしくお願いします。
現在半導体関連に就いております。ここ最近は未熱処理、非アニーリングシリコ ンウェハーのPN反転、抵抗値のことについて調べております。しかし大学の専攻 は半導体と全く関係なく、まわりに物性に詳しい者ももおらず、自分が正しく理 解できているかもわからなくて、メールさせていただきました。
早速ですが、まず私の理解が間違っていないか確認していただけますでしょうか。
- 未アニーリングシリコンウェハーで抵抗縞がある、抵抗値の低いところと高い
ところが同心円状に出るウェハーは、インゴットの引き上げの時の温度によって
酸素ドナーの濃い部分と薄い部分ができてそれが結果的に抵抗縞になる。
- アニールしてないシリコンウェハーの抵抗値はウェハーの温度変化で値が変わ
り、インゴットからスライス、面取り、ラップ、エッチング、ポリシング、エ
ピ、成膜等の各工程の加工中の温度変化でも抵抗値は変化してしまう。
- 未アニーリングのP型シリコンウェハーは酸素ドナーの濃度がP型ドープしたア クセプタ濃度を超えるとN型に反転する。
- 温度変化で抵抗値が変わる=酸素ドナーの量が温度変化で変わる。
- 常温から加熱すると、酸素ドナーは増加する
- N型からP型へ反転は、アニールをしないかぎり反転しない
上記のような認識の上での質問です。
①未アニ―リングウェハーは具体的にどのくらいの温度変化がウェハーに影響ある のか、具体的な温度と抵抗値の関係について教えてください。
②P型がN型に反転してしまう原因、何故酸素ドナーの濃度が濃くなる、増えるの でしょうか。やはりウェハーの温度が関係しているのでしょうか。
③抵抗縞とPN反転に関係性はあるのでしょうか。
未アニーリングシリコンウェハーは加工中に発熱でも影響されると思っておりま す。ただ、PNや抵抗値と温度との関係性がいまいち掴めません。
もし学んでおいた方が良い分野、おすすめの本や文献等もございましたら、ご教 授願います。
以上、よろしくお願い致します。
-----------------------------------------------------------------------------------
Date: Sun, 29 Nov 2020 11:23:44 +0900
A1: M様、佐藤勝昭です。
Q:私の理解が間違っていないか確認していただけますでしょうか。
・未アニーリングシリコンウェハーで抵抗縞がある、抵抗値の低いところと高いところが同心円状に出るウェハーは、インゴットの引き上げの時の温度によって酸素ドナーの濃い部分と薄い部分ができてそれが結果的に抵抗縞になる。
A:そう解釈してよいと思います。
Q:アニールしてないシリコンウェハーの抵抗値はウェハーの温度変化で値が変わり、インゴットからスライス、面取り、ラップ、エッチング、ポリシング、エピ、成膜等の各工程の加工中の温度変化でも抵抗値は変化してしまう。
A:はい、プロセスの温度履歴にによって変化すると解釈されています。
Q:アニーリングのP型シリコンウェハーは酸素ドナーの濃度がP型ドープしたアクセプタ濃度を超えるとN型に反転する。
A:酸素濃度だけのせいかわかりません。
Q:温度変化で抵抗値が変わる=酸素ドナーの量が温度変化で変わる。
A:必ずしもイコールではないと思います。複合欠陥の生成なども関係します。
Q:常温から加熱すると、酸素ドナーは増加する
A:必ずしも増加するとはかぎりません。
Q:N型からP型へ反転は、アニールをしないかぎり反転しない
A:NからPですか?As-implantedのままではアクセプターが活性化せず、酸素ドナーによりNのままですが、これは、inplantationによって結晶格子に 乱れができアモルファスになっているためです。アニールして結晶性を回復すれば、Pになります。
ただし、ドナー濃度が十分低いという仮定の下です。
Q①:未アニ―リングウェハーは具体的にどのくらいの温度変化がウェハーに影響あるのか、具体的な温度と抵抗値の関係について教えてください。
A: 私にはわかりかねます。大口径ウェハに対するRTA(急速アニール)の影響については
論文に詳細な記述があります。
Q②P型がN型に反転してしまう原因、何故酸素ドナーの濃度が濃くなる、増えるのでしょうか。やはりウェハーの温度が関係しているのでしょうか。
A: 多分表面の自然酸化膜から酸素が拡散して酸素濃度が高くなったのではないでしょうか。SIMSで測られたのですか?
Q③:抵抗縞とPN反転に関係性はあるのでしょうか
A: あるとは思いますが、よくわかりません。
------------------------------------------------------------------------------------------------------------
Date: Mon, 30 Nov 2020 14:39:44 +0900
Q2: 佐藤勝昭様
早速の回答ありがとうございます。
実は加工中にPN反転が起きてしまったという過去の事象から、ウェハーとPN抵抗値との関係性を探っておりました。
> Q②P型がN型に反転してしまう原因、何故酸素ドナーの濃度が濃くなる、増えるのでしょうか。やはりウェハーの温度が関係しているのでしょうか。
> A: 多分表面の自然酸化膜から酸素が拡散して酸素濃度が高くなったのではないでしょうか。
> SIMSで測られたのですか?
単純にPN反転が酸素ドナーの影響下にあり、酸素ドナーが温度変化によって生成、または除去されるということを加味した推察です。
残念ながら酸素ドナーに関しての測定実績ありません。酸素ドナーの濃度が増えてP型ドープではあるけれど結果的にN型の動きをする、 酸素ドナーは熱処理を行い正常な状態に戻す、等が記述があったのでそう考えました。公報特許やネットで閲覧可能な文献から調べているので、断片的な情報からの推察になってしまいます。
ただ、佐藤様の言う自然酸化膜を起因とするのであれば、ウェハー表面の酸素濃度が高くなり抵抗値の変化やPN反転が起こると考えると、納得できる気がします。
自然酸化膜の事は完全に抜け落ちていました。また、以下の質問に関しても同様に説明がつくのではないかとも思います。
-----------------------------------------------------------------------------------------------------------------
Date: Mon, 30 Nov 2020 14:58:08 +0900
A2:M様、佐藤勝昭です
。 自然酸化膜の厚みは、1nmの程度です。
MSTのサイト
自然酸化膜の論文
P型ドープを反転するかですが、表面付近では、十分起きうると思います。
ただ、HF処理で簡単に除去できるので、大抵のプロセスでは、自然酸化膜は考える必要がないのです。
確かに表面はガラス状態なので、除去しないと測定に影響が出ます。
-----------------------------------------------------------------------------------------------------------------
Date: Mon, 30 Nov 2020 16:34:41 +0900
AA1: 佐藤勝昭様
自然酸化膜の影響が考えられそうですね。
加工→測定までのあいだでアニール時の様な温度に達することはありませんし、今回HF処理は行っておりませんので、なおさら自然酸化膜の事を考慮しなければ いけないようですね。
お忙しい中、貴重な知見をご教授いただきまして、ありがとうございます。頂いた文献も参考にさせていただきます。
今回は本当にありがとうございました。
-------------------------------------------------------------------------------------------------------------------
Date: Wed, 2 Dec 2020 13:24:22 +0900
A3:M様、佐藤勝昭です。
なんでもQ&Aにアップしたら、読者から次のようなコメントがありましたので、参考にしてください。
--------------------------------------------------------
・真子 隆志
温度でドナーの活性化率が変わるんじゃないでしょうか
---------------------------------------------------------
・松本功
通常だとウエハ中の酸素は石英坩堝からSi融液の自然対流により入ってくるものではないでしょうか?
普通のLSI応用だとアニールして酸素を析出させてイントリンシックゲッタリングのサイトを作らせるのだと思います。
質問者は基板をそのままデバイスにされるようですからパワー用なのでしょうか?
酸素の少ないMCZ結晶を使われているのか?それともCZか?多分MCZ?低濃度ならウエハアニールして酸素を均一に溶融させるか?
--------------------------------------------------------------------------------------------------------------------
Date: Thu, 3 Dec 2020 09:31:02 +0900
AA2:佐藤勝昭様
お世話になっております。Mです。
さすがのQ&A読者様、有識者の方々ですね。
自分では思い浮かばない方面のコメントで、非常にありがたく思います。
是非参考にさせていただきます。
ちなみに結晶はCZのものでした。
-------------------------------------------------------------------------------------------------------------------
1394.非局所配置での純スピン流について
Date: Tue, 17 Nov 2020 09:38:45 +0000Q1: 佐藤勝昭様、初めましてK*大学4年M*田と申します。匿名希望です。
 強磁性体F1、F2と非磁性体Nを図のように非局所配置する。
強磁性体F1、F2と非磁性体Nを図のように非局所配置する。NとF1を電源でつなぐ。強磁性体はアップ電子の方がダウン電子よりも多いスピン偏極した物質なのでF1からNに向けてスピン偏極した 電子が注入されてF1/N界面付近で電子状態は図のように点線(スピン偏極電流が流れる前のフェルミ面)からアップ電子は増加しダウン 電子減少する不均衡が生じる(スピン蓄積)。スピン偏極電流はF1から左側を流れており、F1の右側にはアップ電子が流れていく。
F1/N界面付近ではスピン蓄積が生じているのでこの不均衡を解消するため、アップ電子が流れるとともにその流れとは逆向きにダウン 電子が同じ数だけ流れてきます。この時、電子は互いに逆向き流れてくるので電荷の流れ相殺され、スピンの流れのみが残ります.
この電荷を伴わないスピン流れを純スピン流という(右向きを正とすると、J↑-J↓=2J↑)。純スピン流はスピン拡散長(スピン流を 維持できる距離)を超えた距離では消失し図の右側のNのフェルミ面は一致する。純スピン流はF2へと流入する。この流入した分を、 F2とNの右側を電圧計でつなぐことで電位差として測定する。
ここまでが現時点の理解している限りなのですが、いくつか質問があって、
① F1/N界面で不均衡が生じたときダウン電子が右側から流れてくることで純スピン流が生成されると思うのですが、このダウン 電子はどうやって流れてきたのですか。
F1/N界面付近は電子が注入された分濃度が濃くなってる思うのですが、その濃度が濃い所へ薄い濃度の場所から電子が流れていくこと なんてあるんですか。そもそもF1/N界面付近ではアップ電子とダウン電子のフェルミ面がそれぞれ増加、減少すると参考書資料等で 記述があったのですが、これは正しいですか、二つの電子ともに増加すると考えたいのですが。
② 純スピン流は電荷を伴わない流れと理解しているのですが、電荷が無ければどうやって電位差を測ることができるのですか。
詳しく状況を伝えようと長くなってしまったのですが、ぜひお答えください。
-----------------------------------------------------------------------------------------------------------------------
Date: Tue, 17 Nov 2020 23:10:48 +0900
A1: M君、佐藤勝昭です。 私がくどくど説明するより、九大の木村先生の解説スライド 「純スピン流制御技術とそのデバイス応用」 がわかりやすいです。
あなたの質問(1)ですが
非磁性体NにおいてF1の下の部分とF2の下の部分には電圧差がないので純粋の電流はJc=J↑+J↓=0でなければなりません。
ということは、J↓が逆向きに流れなければならないのです。
質問(2)ですが、化学ポテンシャルの差つまりスピン圧が生じるので電圧として観測されるのです。
------------------------------------------------------------------------------------------------------------------------
Date: Thu, 19 Nov 2020 10:44:52 +0000
Q2: 返信ありがとうございます。
質問1のご返答ですが、電位差がないというのは電流を流す前、NとFを接合して電子が行き来してフェルミエネルギーが一致して電位差 がなくなるということですか。
また添付されてる資料の9ページでは界面付近の非磁性体でアップ電子が増加しダウン電子が減少しているようですが、アップ電子が増加 するのは分かるのですがなぜダウン電子が減少しているのですか。
質問2のご返答ですが、絶対温度T=0では化学ポテンシャル=フェルミエネルギーで、フェルミエネルギーの差を測定しているということですか。
-------------------------------------------------------------------------------------------------------------------------
Date: Wed, 02 Dec 2020 13:17
A2: M君、佐藤勝昭です。
君の質問に十分答える自信がなかったので、九大の木村先生に相談しました。
以下木村先生のご回答です。
前田くんが混乱されているのは、おそらく、半導体物性などの物質のフェルミ準位を考慮した接触電位差と思われますが、 ここで考えている金属では、前提として、平衡状態における全て金属のフェルミ準位は一致しているとして、接触電位差は 無視しています。ですので、強磁性体/非磁性体接合に電圧を加えない状態での電荷の移動はありません。
その後のダウン電子流れが逆向きになる点ですが、 これは、流れを考慮することで、比較的理解しやすくなるのではと思います。
接合から十分離れた非磁性中では、アップとダウンの電子が同じ数だけ流れています。一方で、強磁性体から注入される量に関しては、 スピン偏極しているため、アップが多く、ダウンが少なくなります。
このような状況下で、アップとダウンを同じ数だけ引き出されると、接合近傍で、アップが多くなり、ダウンが少なくなります。
質問2に関してですが、逆に混乱するかもしれないのですが、純スピン流の電圧検出には、強磁性体(電圧端子)が必要です。
強磁性体では、電気伝導率がアップとダウンで異なります。アップが右向き、ダウンが左向きに同じ数だけ流れているような 純スピン流では、右向きに発生する電位差と左向きに発生する電位差が異なるため、電圧が発生することになります。
参考スライド(アニメーション)を見てください。
---------------------------------------------------------------------------------------------------------------------------
Date: Tue, 8 Dec 2020 10:46:29 +0000
AA: 佐藤先生、木村先生
お忙しいなか質問に答えていただきありがとうございました。添付された資料を参考に続けて勉強していきます。
----------------------------------------------------------------------------------------------------------------------------
1395.セラミックスの誘電率の温度依存性について
Date: Fri, 11 Dec 2020 00:23:23Q1: 東京農工大学名誉教授、佐藤勝昭 先生
初めまして、S*大学理学部化学科4年のF*と申します。
先生のHPを拝見し、質問させて頂きます。
恐縮ですが、HP掲載の際は、匿名でお願い致します。
私は、セラミック薄膜の作製および特性評価に取り組んでおります。
そこで、セラミックスの誘電率の温度依存性について教えて頂きたいです。
強誘電体では、キュリー・ワイスの法則が成り立ちますが、常誘電体の温度依存性についても、 何か定式化されたものがあるのでしょうか。具体的には酸化ジルコニウム(ZrO2)について知りたいです。
私が調べた限りでは見つけることができませんでした。
また、セラミックスの誘電率の温度依存性に関しましてデータブック等がございましたら重ねて教えて頂きたく存じます。
お忙しいところ大変恐縮ですが、何卒よろしくお願い申し上げます。
----------------------------------------------------------------------------------------------------------------------------
Date: Sat, 12 Dec 2020 00:24:13
A1: F君、佐藤勝昭です。
常誘電体の誘電率の温度依存性については1960年代に研究されています。
B. D. Silverman and R. I. Joseph: Temperature Dependence of the Dielectric Constant of Paraelectric Materials, Phys. Rev. 129, 2062 (1963)
これは強誘電体の常誘電相での温度変化を論じているので、酸化ジルコニウムに適用できるかどうかわかりませんが。図書館で調べてみてください。
光学フォノンが関与していると温度依存性がないようです。
------------------------------------------------------------------------------------------------------------------------------
Date: Mon, 14 Dec 2020 00:18:10
AA!: 佐藤先生、S大学のFです。
早速のご返答ありがとうございます。また、返信が遅くなり申し訳ございません。教えて頂いた文献をもとに勉強したいと思います。
お忙しい中、本当にありがとうございました。
-------------------------------------------------------------------------------------------------------------------------------
Date: Thu, 17 Dec 2020 15:57:27
A2: F君、佐藤勝昭です。
先日質問いただいたときは、ちょうどナノテクノロジー総合シンポジウムの最中で、忙しくしていたので、古い文献をお伝えするだけの大雑把な回答になりごめんなさい。
添付するのは、佐藤勝昭編著「応用物性」(オーム社1989)の第4章p166-168です。
誘電率εは分子分極率αを使って、クラウジウスモソッティの式で与えられます。
(ε-ε0)/(ε+2ε0)=Nα/3ε0
比誘電率εrを使って書くと
(εr-1)/(εr+2)=Nα
と書けますから、比誘電率の温度変化を知るには分子分極率αの温度変化を求めなければなりません。
分子分極率は、電子分極率とイオン分極率の和で決まります。
★シリコンなど共有結合性の絶縁物の場合分極率は電子分極率のみで与えられます。
直流の比誘電率εr(0)はバンドギャップEgの関数で
εr(0)=1+A/Eg2
で与えられ、比誘電率の温度変化はバンドギャップの温度依存性を通じて起きます。
バンドギャップの温度変化は、電子格子相互作用でもたらされ、デバイ温度(格子振動の平均エネルギーに相当する温度)より十分低い温度では、温度の二乗で変化します。
Eg=Eg0-βT2とすると
εr(0)=1+A/(Eg0-βT2)2~1+(A/Eg02)(1+2βT2+・・)
温度上昇とともにわずかに大きくなる程度です。
★イオン性の物質の場合、分子分極率はイオン分極の寄与が大きくなります。永久双極子の配向によって説明され、添付文書の(4.44)式(p168)のように複雑な式になります。
--------------------------------------------------------------------------------------------------------------------------------
Date: Fri, 18 Dec 2020 08:13:26
Q2: 佐藤先生、お世話になっております。S大学のFです。
お忙しい中、詳細なご回答を頂きありがとうございます。
私の研究では、セラミックスの薄膜材料を用いています。
したがって、分子分極としては、
①界面分極 ②配向分極 ③イオン分極 ④電子分極
の4種類を考えています。
主として、酸化ジルコニウム(ZrO2)を使っています。結晶構造は立方晶または正方晶であるため、配向分極の寄与は小さいと考えております。
また、交流測定により誘電率を測定しています。
測定周波数は1 Hz~1 MHzであるため、4種類の中では、界面分極の寄与が最も大きいと考えています。
界面分極では、セラミックスなどの多結晶体において、空間電荷が欠陥や粒界に捕捉されることで生じると認識しております。
空間電荷(正負のイオン)の移動は、不純物半導体と同様の挙動を示すと予想しております。
したがって、界面分極の温度依存性はアレニウスの式に従うと考えておりますが、この考え方は正しいでしょうか。
お忙しい中、お手数をおかけし大変恐縮ですが、ご教授頂ければ幸いです。何卒よろしくお願い申し上げます。
-------------------------------------------------------------------------------------------------------------------------------------
Date: Sat, 19 Dec 2020 21:10:27
A2: F君、佐藤勝昭です。
よく勉強していますね。自分でそこまで考察できるのは素晴らしいです。
たしかにZrO2のようなセラミックスでは界面分極の寄与が大きいですね。
空間電荷(正負のイオン)の移動は、不純物半導体と同様の挙動と考えて いいでしょうね。トラッピングに関してはアレニウス型でよいと存じますが セラミックスの場合の空間電荷の移動は、半導体とは違って極めて遅い現象 なので、交流測定ではうまく測れないかもしれませんね。
--------------------------------------------------------------------------------------------------------------------------------------
Date: Mon, 21 Dec 2020 02:35:49
AA2: 佐藤先生、お世話になっております。
S大学のFです。
教えて頂きました通り、空間電荷のトラッピングに関しましてアレニウス型で考察を進めていきます。
これらは、私の卒業研究の一環です。インピーダンスアナライザーを用いたセラミック薄膜の交流測定は、今年から始めたばかりであり、 測定や考察は手探りの状態です。従いまして、専門家である佐藤先生に相談させていただいた次第です。
お忙しいところ、懇切丁寧にご回答頂き、感謝申し上げます。本当にありがとうございました。
--------------------------------------------------------------------------------------------------------------------------------------
1396.局在プラズモンに関する疑問について
Date: Wed, 3 Mar 2021 19:19:40Q: 佐藤勝昭 先生
はじめまして、高校で理科教員をしているE*と申します。
大学では化学を専攻していました。(掲載の際には匿名にして頂ければと思います。)
ホームページの質問コーナーを見て、メールを送らせて頂きました。
最近プラズモンに興味を持ち、佐藤先生の公開されている資料も拝見させて頂いています。
そんな中で、以下のような疑問が浮かびました。
とりわけ局在プラズモンに関してですが、レーザー光のように同位相で連続的な光と金属が共鳴することは理解できます。
しかしながら、自然光のように位相が不揃いで不連続な光と共鳴するイメージが掴めずにいます。
具体的には、自然光の電場によって金属内の電子振動が誘起された時点で、光子は吸収・散乱などによって消滅し、 この時点で次の(逆位相の)電場を金属は感じられなくなり、周期性がないので共鳴は生じないのではないかという疑問です。
思い返してみれば、これまで「光は粒子と波の性質を持つ」という文言を受け入れてきましたが、 いざプラズモンを理解するために一つの光子と金属の相互作用を考えた時、波としての性質をどう理解すればよいのか悩んでしまいます。
先の疑問は、電磁波の一つの波(電場)が電子と相互作用した時点で光子が消滅するという前提の上にありますが、そもそもこの考え自体が正しい ものなのか不安でもあります。
また、仮に相互作用の後すぐに光子が消滅するわけでないとすると、今度は1つの光子に対応する波は複数の節(=一定の長さ)を持っているのか という疑問が湧いてきます。
数式を用いて厳密な議論をすれば解決する疑問なのかもしれませんが、恥ずかしながらそこまで理解が進んでおらず、ご助力いただけないでしょうか。
--------------------------------------------------------------------------------------------------------------------------------------
Date: Wed, 3 Mar 2021 23:00:15
A: E先生、佐藤勝昭です。
局在プラズモンは、波長より十分小さい直径の金や銀の粒子において観測されます。
どのような位相の光であれ、光の電磁波で電子は直ちに動いて逆向きの電界を作り もとの電界を遮蔽してしまうので、光は伝播できなくなり局在するのです。このこと が起きる特定の周波数を局在プラズモン共鳴周波数と呼んでいます。
波長に比べ十分小さいので自然光の波束と波束の間に位相の違いがあっても、1つの 波束毎に共鳴するのです。
局在プラズモン共鳴については、岡本隆之先生の解説 をご参照ください。
--------------------------------------------------------------------------------------------------------------------------------------
Date: Thu, 4 Mar 2021 22:54:50
AA: 佐藤先生
さっそく返信頂きありがとうございます。
中々資料を入手できる環境にないので、解説の提供大変ありがたいです。
頂いた資料も参考に勉強を進めたいと思います。
--------------------------------------------------------------------------------------------------------------------------------------
1397.油絵具に生じる金属石鹸について
Date: Thu, 11 Mar 2021 11:21:58Q1: 佐藤勝昭先生
初めてご連絡差し上げます。T*大学院博士一年のK*と申します (掲載の際には匿名にして頂ければと思います)。
ホームページの質問コーナーを見て、メールを送らせて頂きました。
以前より油絵具に生じる金属石鹸について興味を持っており、先生の 『絵画技法と画材の話』のパワーポイントを拝読いたしました。
描画時の問題として、ワックスメディウムを多用すると金属石鹸が形成され、剥離に至るとの記載がございました。
蝋と顔料で金属石鹸ができるという話は聞いたことがなく、どういった化学的メカニズムで生じるのでしょうか?
もしくは、ワックスが油絵具の酸化重合を邪魔してしまう、もしくは金属石鹸を加速させてしまうことで、剥離がおきやすくなるということなのでしょうか?
ご教示のほど、よろしくお願いいたします。もしも、それに関する参考文献などがございましたら、併せてご教示いただきたく存じます。
お忙しいところお手数をおかけいたしますが、どうぞよろしくお願いいたします。
---------------------------------------------------------------------------------------------------------------------------------------
Date: Thu, 11 Mar 2021 19:58:43 +0900
A1: K様、佐藤勝昭です。
メールありがとうございます。
油絵の解き油は乾性油とよばれ、脂肪酸エステルです。
エステルというのは酸とアルコールが反応して水を失ったものです。
例えばリンシードオイルの成分は約60%がリノレン酸という脂肪酸です。(1)
ジンクホワイトの酸化亜鉛粒子はリノレン酸と鹸化反応して金属石鹸を つくると考えられていました。(2)
しかし、小杉らの研究によれば、酸化亜鉛の存在によってπーアリル中間体 を形成し、吸着酸素と反応して、石鹸をつくり、脂肪酸のC-C結合を切る と言うことがわかっています。(3)
詳細は、添付の文献(3)をお読みください。
-------------------------------------------- (1)ホルベイン工業:絵具の科学 p57,(中央公論美術出版 2004)
(2)牧島, 豊田, 岡村:色材, Vol44, p156 (1971)
(3)小杉, 廣田:色材, Vol.72 No.10, p613 (1999)
-----------------------------------------------------------------------------------------------------------------------------------------
Date: Thu, 11 Mar 2021 20:27:19
Q2: 佐藤勝昭先生
ご返事いただきありがとうございます。
また、乾性油の金属石鹸の生成メカニズムについてご教示いただきありがとうございます。
詳細まで存じておりませんでしたので、とても勉強になりました。参考文献も読ませていただきます。
ただ、質問メールの私の説明に問題があり、お聞きしたいことがちゃんとお伝えできていなかったようでした。本当に申し訳ございません。
お聞きしたいのは、「金属石けんの形成(ワックスメジウムの多用)」の部分で、ワックスを加える(加えすぎる)ことが、金属石けんの生成に どのように影響を与えるのかについてです。お手数をおかけいたしますが、こちらについてもご教示いただけますと幸いです。
お忙しいところ大変恐縮ですが、どうぞよろしくお願いいたします。
------------------------------------------------------------------------------------------------------------------------------------------
Date: Thu, 11 Mar 2021 20:40:29 +0900
A2: K様、佐藤勝昭です。
すみません。早とちりして、質問をちゃんと読んでいませんでした。
ワックスが石鹸化に関係するかという質問ですが、確かに調べても根拠となる文献は見つかりませんでした。
絵具の科学p194をよく読むと、ワックスが金属石鹸をつくるとは書いてませんね。「金属石鹸やワックス分は絵具の粘りに影響を与えるが、 付着力は低下させる」と書かれています。
私の間違いです。スライドを修正する必要がありますね。ご指摘ありがとうございます。
------------------------------------------------------------------------------------------------------------------------------------------
Date: Thu, 11 Mar 2021 21:11:38
AA: 佐藤勝昭先生
早々にお返事ありがとうございます。
そうだったのですね。理解が進んでよかったです。
この度は、ご丁寧にありがとうございました。
------------------------------------------------------------------------------------------------------------------------------------------
1398.キュリー温度が低温の磁性材料
Date: Fri, 30 Apr 2021 06:40:00Q: 佐藤勝昭様、S*社のS*と申します。HPを拝見し、ご連絡させていただきました。
Q&Aにご掲載いただく際は匿名でお願い致します。
磁石の温度をキュリー温度に対して上下させることで磁気相転移により磁場の発生の切り替えを行うデバイスを考えており、 その磁石の候補材料として、キュリー温度が低温(10K~30K程度)の磁性体を探しております。
佐藤様の資料から、元素単体では、ホロミウム、エルビウム、ツリウムが候補と成り得ると考えております。
しかし、プロセスの観点からは、元素単体の使用よりも、化合物での使用が容易であると予想しております。
お聞きしたいことは、上記で述べた材料の他に、単結晶または化合物で下記の条件を満たす材料をご存じでしょうか。
・キュリー温度が低温(10K~30K程度)
・飽和磁化がある程度の大きさ(例えばエルビウムの飽和磁化~3Tに近い、またはそれより小さくても大幅には減少しない)
また、これらの材料に関して、参考となる資料がございましたら、そちらも併せてご教授いただけますと幸いです。
-------------------------------------------------------------------------------------------------------------------------------------------
Date: Sat, 1 May 2021 15:52:23
A: S*様、佐藤勝昭です。
「キュリー温度が低温(10K~30K程度)」の強磁性体で、元素単体でない化合物 ということで、磁性体ハンドブックの初版(朝倉書店1975)が手元にあったので調べて 見ましたが、Tc=10-30Kは少なく、もう少し広げて調べました。
飽和磁化については、データがみつけられません。
| 物質名 | 磁性 | キュリー温度(Tc) | 文献 |
|---|---|---|---|
| Ti0.87Co2.13 | 強磁性 | 44K | Y.Aoki et al. JPSJ 21, 565 (1966), T.Nakamichi et al. JPSJ 28, 590 (1970) |
| Nb0.765Co2.35 | 強磁性 | 16K | 伊藤寛他:日本物理学会27回年会予稿 物性B37 (1972) |
| Ta0.765Co2,235 | 強磁性 | 19K | H.Itoh et al., Z. Metallkde 65, 149 (1974) |
| ZrZn2 | 強磁性 | 35K | B.T.Mattias, R.M.Bororth PR 109, 604 (1958) |
| PrAg | 強磁性 | 14K | J.Pierre, R.Pauthenet CR Acad Sci 260, 2739 (1965) |
| NdAg | 強磁性 | 21K | J.Pierre, R.Pauthenet CR Acad Sci 260, 2739 (1965) |
| ErZn | 強磁性 | 50K | K.Kanematsu et al. JPSJ 26, 244 (1969) |
| ErCo | 強磁性 | 39K | R.M.Moon et al. JAP 36,978 (1965) |
| MnSi | 遍歴らせん磁性体 | 38K | D.Sjoda JPSJ 21, 555 (1966) |
| Co(S0.9Se0.1)2 | 強磁性 | 42K | K.Adachi et al. JPSJ 26, 631 (1969), K.Adachi et al. JAP 39, 1343 (1968) |
| Ag0.5In0.5Cr2Se4 | 50K | 強磁性 | H.L.Pinch et al. Mat. Res. Bull 5, 425 (1970) |
HgCr24| メタ磁性 | 36K | P.K.Baltzer et al. PRL 15, 493 (1965) | |
| EuO | 強磁性 | 77K | B.T.Matthias et al. PRL 34, 160 (1961) |
| EuS | 強磁性 | 16.27K | W. Stutius Phys Kond. Mat. 4, 341 (1969) |
| CrBr3 | 強磁性 | 32.844K | I.Tsubokawa JPSJ 15, 2109 (1960),J.T.Ho et al. PRL 22,1270 (1969) |
| MnCr2O4 | フェリ磁性 | 55K | N. Menyuk et al. JAP 33, 1144 (1962) |
Date: Wed, 12 May 2021 01:53:06
AA: 佐藤勝昭 様
S会社のSです。返信が遅くなり大変申し訳ありません。
丁寧なご回答、ありがとうございます。
いただいた磁性材料のリスト、大変参考になりました。
教えていただいた文献と併せて他の文献も調査したところ、 飽和磁化、信頼性ともに良さそうな候補をいくつか見つけることができました。
本当にありがとうございます。
今後ともどうぞ宜しくお願い致します。
--------------------------------------------------------------------------------------------------------------------------------------------
1399.超伝導体の光学伝導度の虚数部について
Date: Thu, 27 May 2021 01:06:00 +0000Q: 佐藤勝昭先生、初めまして。 Y*大学工学部4年T*と申します(匿名希望でお願いします)。 現在,超伝導の光物性(テラヘルツ波に誘起された非平衡ダイナミクス)について調べているのですが、その中で,複素光学伝導度がいまいち理解できません。
複素光学伝導度のうち,実部は光学伝導度のスペクトルとして用いられるのに対し、虚部の表す意味についてははっきりをその物理的意味が書かれた文献は見られませんでした。
ただ、光学伝導度の虚部が超伝導(超流動)密度に比例した値であるという記述が見られました.そこで,光学伝導度の虚部が直接的に物理的意味を示すのかどうかを知りたいということと,どのようなモデル(理論)から出発すると虚部が超流動(超伝導)密度に繋がるのかおおまかでいいので教えていただけたら幸いです。
お忙しいところ恐縮ですが,お願いいたします。
----------------------------------------------------------------------------------------------------------------------------------------------
Date: Thu, 27 May 2021 14:48:58
A: T君、佐藤勝昭です。
4年生なのに、むずかしい課題に取り組んでいるのですね。基本的には、卒業研究の指導教員の先生に尋ねるべきです。
ここでは、ヒントを差し上げましょう。添付の教科書と解説論文を勉強してください。
(以下の回答は、長岡技術科学大学石橋隆幸教授のご協力によります。)
-----------------------------------------------------------
ティンカムの教科書「超伝導現象」のp67に複素光学伝導度σ=σ1-iσ2の表式が式(2-96a,b)に出ており、その下に 磁束侵入長λとの関係が示唆されています。
また、田島先生の解説の式7のとおり、光学伝導度の虚部は、ロンドンの磁場侵入長、または、超伝導電子の密度を表して います。この関係は、ロンドン方程式から出てきています。
----------------------------------------------------------------------------------------------------------------------------------------------
Date: Thu, 27 May 2021 07:01:10
AA: 佐藤先生、返信ありがとうございます。
そうですね,担当の先生に尋ねるのが最優先だと思います。その点は申し訳ございません。
添付資料読ませていただきました。光学伝導度の虚部から超伝導プラズマ周波数を割り出せて,超伝導プラズマ周波数と超伝導密度を結ぶ(磁場侵入長についての)関係式を踏まえれば, 光学伝導度の虚部から超伝導密度を結びつけることができるのですね。
これからロンドン方程式について勉強しようとしていたところでしたので,ロンドン方程式から光学伝導度の虚部と超伝導密度を結びつけるまでの流れを調べてみたいと思います。
これで調べ学習が一歩前進しました。お忙しい中ありがとうございました。
----------------------------------------------------------------------------------------------------------------------------------------------
1400.ユーロピウムの実際の材料での使用例・応用例について
Date: Fri, 2 Jul 2021 21:31:39Q1: 東京農工大学 佐藤勝昭先生
始めまして。HPを拝見しました、東京農工大学工学部化学物理工学科3年のSと申します。(名前のみ匿名でお願いいたします。)
私が履修している電気電子材料工学という講義内で、材料(元素ごと)を調べまとめるという調査発表があります。調査内容に物質名・応用分野・構造・特性・歴史等があるのですが、その中で使用者の情報(農工大の専門の先生にインタビューして専門家ならではの解説記事をとり編集して掲載する)という項目があります。
私が担当する元素・材料はEu:ユーロピウムなのですが、佐藤先生が材料・物性、半導体関係の専門であることを知りメールを送らせていただいた次第でございます。
ユーロピウムについて、実際の材料での使用例・応用例や現在の研究例等をご存じでしたらご教示いただけないでしょうか。お忙しい中、不明瞭で具体的でない質問で恐縮ですが、お答えをいただければと存じます。
-------------------------------------------------------------------------------------------------------------------------------------------------
Date: Sat, 3 Jul 2021 00:10:30
A1: S君、佐藤勝昭です。
Eu:ユーロピウムについては、私にとって思い入れのある元素です。
私は農工大に来る前はNHK基礎研にいたのですが、研究対象として磁性半導体を研究していました。
磁性半導体としてEuS(硫化ユーロピウム)を研究していました。EuSはキュリー温度が16.7Kの強磁性体です。
融点が2250℃と高く、高温高圧下で結晶を作りました。
日本物理学会秋の分科会1969.11.16で
中山忠久,佐藤勝昭,寺西暎夫:「EuS単結晶の成長と電気光学的性質」
という発表をしましたが、論文は書いていません。
1984年に農工大に赴任したのち、いろんな研究をしましたが、発光材料の発光中心としてのEuも研究しました。
Euはカラーテレビブラウン管で赤の発光中心として使われていました。赤の発光はf→d遷移によるものです。
CaS:Euの発光の磁気円二色性スペクトルの研究論文があります。
・K. Hayata, N. Iwata, K. Hasegawa, K. Sato:Temperature Dependence of Magneto-Optical Spectra in EuO Epitaxial Films; 日本応用磁気学会誌25 [3-2] (2001) 299-302.
Zoomで議論してもいいですよ。
-------------------------------------------------------------------------------------------------------------------------------------------------
Date: Mon, 5 Jul 2021 12:05:19
Q2: 佐藤勝昭先生、農工大科3年のSです。ご返信ありがとうございます。
挙げていただいた論文のうちWeb上で閲覧可能なものは拝読させていただきました。農工大内でもユーロピウムの研究が行われていたということは大変興味深いです。
Zoomでの議論の提案は大変嬉しいのですが、私は化学物理工学科の化学工学コース所属のため半導体材料についての基礎知識(バンド理論等)が十分ではありません。
そのため、せっかくZoomの機会をいただいても議題を理解したり質問をする自信がありません。
(稚拙な表現ですが、分からないことが分からないという状態となる可能性が高いです。)
誠に勝手ですが、頂いた論文を熟読させていただきより詳しく知りたいことを発見したら再度メールさせていただこうと思います。
この度はお忙しい中たくさんの資料・論文をいただき、感謝申し上げます。
ありがとうございました。
------------------------------------------------------------------------------------------------------------------------------------------------
Date: Tue, 6 Jul 2021 08:57:19
A2: S君、佐藤勝昭です。
「半導体材料についての基礎知識(バンド理論等)が十分ではありません」とのことですが、化学の学生でも、半導体のバンドモデルの概略くらい知っておかないと現代社会で通じません。
添付は、私が日本磁気学会誌に連載した「超入門ようこそマグネの国に」の第3回ですが、その付録A(p184)に「バンドモデルの手ほどき」を参考に勉強してください。
(以下は、ちょっと難しいかもしれませんが、我慢して最後まで読んでください。)
なお、半導体にわずかに添加された遷移金属や希土類元素の電子状態はバンドモデルでは表すことができません。半導体や金属のs,p電子は結晶全体に広がった波で表されるのですが 遷移金属のd電子や希土類のf電子は、原子核のクーロン力に強く束縛されて、原子のそばに局在しています。すると、電子の間のクーロン反発力も強く働くので、多重項で表される 状態になります。遷移金属イオンのd電子の場合は、配位子(遷移金属に結合したアニオン)との共有結合の影響で多重項の電子準位が分裂します。これは配位子場分裂と呼ばれます。
一方、希土類イオンの4f電子はほとんど配位子との結合がないので、孤立原子の状態に近い多重項が保たれます。それで、希土類の発光は鋭い線スペクトルを示します。
ただユーロピウムでは、局在した4f電子と配位子と結合した5d電子の間の光学遷移があり、f→d遷移はパリティ許容なので強い発光が起きます。d電子のエネルギーは幅をもつので、 発光は線スペクトルではなく、ブロードな発光帯となります。
ルミネッセンスについては、私の講義スライド「基礎から学ぶ光物性」第9回 第1部 ルミネッセンスとは を読んでください。中に希土類の発光もあります。
------------------------------------------------------------------------------------------------------------------------------------------------
1401.ヘマタイトの条痕について
Date:Mon, 9 Aug 2021 14:05:15Q: 佐藤勝昭 様、N*社に所属しているN*と申します。
HPを拝見し、物性Q&Aコーナーで質問させていただきたく、連絡いたしました。
会社の業務と直接は関係なく、私の興味の範囲の内容ではありますが、所属・氏名と添付図は非公開とさせていただけないでしょうか。
条痕色とFe2O3のラマンスペクトルに関して2点質問させてください。
Fe2O3(ヘマタイト)はバルクでは黒色~灰色ですが、粉砕すると赤色を呈します。
○1つ目の質問
鉱物学では条痕と呼ばれる現象のようですが、条痕のメカニズムは各物質で明確に説明できるものなのでしょうか?
粒径が変われば表面での反射や、界面での屈折、光路長による吸収など様々な効果が変化するとは思いますが、簡単に調べた範囲では曖昧な説明が多いように見えます。
○2つ目の質問
条痕色に伴って、もしくは50μm~数μmの範囲での粒径変化により、ラマンスペクトルが大きく変化が生じるようなことはあるのでしょうか?
<背景>
数mmの粒径の灰色のヘマタイト試薬を粉砕してみました。
粉砕すると、光学顕微鏡でもわかるレベルで、10μm程度を境に赤色に見える粒子が現れます。
この際、粉砕前の黒色時のラマンスペクトルと、粉砕後の赤色部のラマンスペクトルには大きな違いがあります。
赤色部は、粉砕前の黒色と比較すると、10~30cm-1ほど低波数側にシフトし、ピーク強度比も大きく変化し、見かけのピークの本数にも違いが生じます。
私の感覚だと、一見別な物質だと判断してしまうほどの差があります(添付図:非表示)。
なお、XRD的には不純物や相変化は全く認められず、粉砕前後でピーク位置や半値幅もほぼ変わりません。そのため、格子定数や結晶性に大きな変化は生じていないと思います。 また、粉砕前でもランダムパターンに近いため、粉砕前でも多結晶であり、結晶粒径はそれなりに小さいようです。
条痕は構造色の一種であり、エネルギー準位が変わることはないと考えていたのですが・・
このオーダーでの粒径差でラマンスペクトルが変化する場合があるとすれば、実用上、想定しておかなければならない現象かと思いました。
原因に関する文献は私の方では見つけられていませんが、例えば、論文では複数のヘマタイト試料のラマンスペクトルを掲載していました。
Fig.6に単結晶、鉱物標本、合成粉末のラマンスペクトルが掲載されていますが、私の方で確認した粉砕前は文献の単結晶や鉱物標本、粉砕後は文献の合成粉末にそれぞれ近いです。
この文献ではラマンスペクトルの違いが、化学量論、結晶性、粒径などに起因すると述べられていますが、私の実験では粉砕処理しただけなので、化学量論的な差はないと思います。
以上質問になります。
初歩的な内容かもしれませんが、助言いただければ嬉しいです。
---------------------------------------------------------------------------------------------------------------------------------------------
Date: Mon, 9 Aug 2021 16:28:37
A: N様、佐藤勝昭です。
 α-Fe2O3は昔から赤色塗料として知られています。
α-Fe2O3は昔から赤色塗料として知られています。従って、本来この物質は、赤色光を透過します。
光触媒としての研究論文によれば添付図のように600nmから短波長に向かって増加する光吸収が見られます。透過光は赤色です。
粉砕して粒子が小さくなれば、透過光が散乱して赤く見えるのでしょう。この吸収端のTaucプロットからバンドギャップは2.75eVとされています。
一方、最近の理論によれば、光吸収の原因は配位子の酸化物イオンからFe3+への電荷移動遷移とされています。
(*Simone Piccinin: The band structure and optical absorption of hematite (α-Fe2O3): a first-principles GW-BSE study; Physical Chemistry Chemical Physics Issue 6, 2019)
ヘマタイトは光触媒としても知られます。
光触媒に光が照射されると、触媒表面に電子と正孔 (電子が抜けた孔) が生成し、この電子が水の水素イオンを還元することで水素が生成します。
粉砕の途中で光触媒反応が生じれば、空気中の水分を分解してOH-が生じ、XRDにはかからない極めて微量のFeOOH, Fe(OH)2などを生じる可能性があります。
そのあたりを調べてみませんか?
---------------------------------------------------------------------------------------------------------------------------------------------
Date: Wed, 11 Aug 2021 08:45:50
AA: 佐藤勝昭 様、ヘマタイトの色に関して質問をしましたNです。早速の回答ありがとうございました。
頂いた参考文献も知りませんでした。
電荷移動遷移とは、なんとなく錯体に特有のものだと思っていましたので意外です。
ご指摘頂いたように、粉砕前後で別な物を見てしまっている可能性を考慮してみます。
まずはXPSあたりで最表面の情報を比較してみようかと思っています。
この度は有意義なアドバイスを頂きまして、ありがとうございました。
---------------------------------------------------------------------------------------------------------------------------------------------
1402.非反射膜の干渉について
Date: Thu, 16 Sep 2021 23:08:54Q: K*と申します。HPを見ての質問です。先生のHPは学生時代から参考にしておりました。HPに乗せる際は匿名でお願いします。
技術系の会社員をしていますが、この質問は会社の業務とは関係なく個人的に疑問になってしまった質問です。
質問と回答をHPに掲載することにはまったく問題はありません。
ご回答いただければありがたく、よろしくお願いします。
----------------------------------------------------------------------------------
 反射防止膜がなぜ反射光を防ぐかについて
反射防止膜がなぜ反射光を防ぐかについて(A)光が反射率0の反射防止膜に入射したとする。
(B)例えば半分の光が表面で反射します。この表面反射光は位相がずれないとする。
(C)もう半分が基板表面で反射します。これを裏面反射光とします。コーティングは、裏面反射光が半波長だけ表面反射光とずれるように設計されている。
(D)表面反射光と裏面反射光は位相がちょうど半波長ずれているので、互いに干渉して弱めあって消滅します。
上記(A)(B)(C)(D)の説明をよく見ますし、これはこれで納得できます。
しかし、この場合、表面反射光のエネルギーと裏面反射光のエネルギーとが打ち消しあって消えてしまうことになります。これはエネルギー保存則に反しているのでは?
これに対して、
「そもそも表面反射光も裏面反射光も現実には発生してはいない。説明のため、便宜的に波を描いただけで実際は入射光は基板に吸収されて熱になるか、基板が透明なら基板を透過していくだけ。だからエネルギー保存則に反してはいない」、と解釈しました。
しかしながら、この解釈の場合、表面反射光も裏面反射光もなぜ発生しないかがわかりません。自分が入射光の立場だとして、コーティングの表面にさしかかったとき、「あ、ここで反射してしまうと、将来は位相が半波長ずれた裏面反射光とであって消滅してしまうぞ、だから、ここは反射せずに直進しよう(屈折はするが)」と知っていないとこのような挙動にはならない気がします。
この解釈のどこが間違っているのか、どう考えると整合性がとれるのか教えていただけないでしょうか。
------------------------------------------------------------------------------------------------------------------------------------------------
Date: Fri, 17 Sep 2021 06:48:53 +0900
 A:K 様、佐藤勝昭です。
A:K 様、佐藤勝昭です。レンズの反射防止コーティングを考えて下さい。
コーティング膜とレンズの界面側へ入射光は全部透過するので、明るいレンズになります。
同じことが基板との界面を考えて下さい。基板側に伝わった光はバンドギャップを超えておれば全部吸収されます。
従って、エネルギー保存則に反することはありません。
★同様の疑問について「レンズコーティングはなぜ反射を抑え透過率が上がるのか?」というサイトにわかりやすい説明があります。
ここではレンズですが、これを基板に置き換えれば、「エネルギーが反射されず基板に到達して吸収され、太陽電池がよく発電する」ことがわかります。
------------------------------------------------------------------------------------------------------------------------------------------------
1403.磁気余効(ディスアコモデーション)についてて
Date: Tue, 1 Mar 2022 04:17:21Q: 佐藤勝昭様, お世話になります。
HP見ての質問でございます。A社のOと申します。Webにアップする場合には匿名を希望いたします。
以前、磁性微粒子の高周波特性ではご解説ありがとうございました。
本日は磁気余効(ディスアコモデーション)について質問があります。
-------------------------------------------------------------------------------------------------------------------
フェライト粒子と樹脂を混合し、加熱、加圧した成形体なのですが、その成形体を数日間あるいは数週間放置しておいて比透磁率が小さくなっていく現象を確認しました。
これをディスアコモデーションかと思っての質問でございます。
1,磁性体ハンドブックなど見ていますと、秒~分単位での透磁率低下は記載がありますが、上記のような期間でのディスアコモデーションは起きうるのでしょうか?
2,緩和時間の式は見ましたが、どの程度の期間で収束するか、粒子径、組成などよって決まっているでしょうか?
3,高温高湿など環境試験にいれることで透磁率低下を加速して確認することはできるのでしょうか?Yesの場合、どのような条件が好ましいでしょうか?
以上、宜しくお願い申し上げます。
-------------------------------------------------------------------------------------------------------------------------------------------
Date: Thu, 3 Mar 2022 12:02:29 +0900
A: Oさま、佐藤勝昭です。
メールありがとうございます。磁気余効に関するご質問ですが、私の専門範囲を超えますので、磁気記録材料の磁気余効に詳しい大橋啓之先生(早大)にお伺いしました。
大橋先生からのお返事は以下の通りです。
----------------------------------------------------------------------------------------------------
太田恵造「磁気工学の基礎Ⅱ」の 8.2節に沿った形で回答させていただきます。
>1.磁性体ハンドブックなど見てますと、秒~分単位での透磁率低下は記載がありますが、上記のような期間(数日間あるいは数週間)でのディスアコモデーションは起きうるのでしょうか。
←Richter型は、横軸に時間の対数をとった時の透磁率(ディスアコモデーションの場合)あるいは磁化(磁気余効の場合)の変化が大きい時間範囲において緩和時間分布が一様だと仮定する現象論です。
緩和時間は多くの場合温度に対して指数関数的な依存性を持っており、太田先生の本にも「µi - lnt 曲線は測定温度を高くすると左方へずれ、温度を低くすると右方へずれる」(p.324)と書かれています。
また「ディスアコモデーションの曲線全体を描くには t = 0 から t = ∞ までの時間を必要とするので、実際問題として測定が困難であるから、数分~数十分程度の測定が行われている」(p.328)とも書かれています。
さらに、Mnフェライトについてディスアコモデーション係数(一定の時間間隔での透磁率の低下量)の温度依存性を調べた Krupičkaのデータ(図8.2-3)から複数の機構がディスアコモデーションに関わっていることが示されています (ご参考に同じデータが示されている S. Krupička and K. Závěta, Magnetic Aftereffects in Ferrimagnetic Oxidic Spinels, Journal of Applied Physics, 39, 930, 1968 をメールに添付しておきます)。
高い温度で現れるディスアコモデーションの常温での緩和時間は、数週間またはそれ以上の長いものになると考えられます。
>2.緩和時間の式は見ましたが、どの程度の期間で収束するか、粒子径、組成などによって決まっているでしょうか。
>3.高温高湿など環境試験に入れることで透磁率低下を加速して確認することはできるでしょうか。
←フェリ磁性の研究でノーベル賞を受賞した Néelは磁気余効果の研究の開拓者でもありました。
彼は磁化率(透磁率)の可逆成分と不可逆成分を区別することの重要性を指摘しており、熱揺らぎ磁気余効が不可逆磁化率と深く結びついていることを指摘しています。
磁気余効における粒子径の影響を説明するのに単磁区粒子の集合モデルが使われる場合があります。
このモデルを使えば粒径や磁気異方性の効果が計算できますが、交換結合の効果等によりそのようなモデルはあまり適切ではないことが分かっています(注1)。
一方、ディスアコモデーションは可逆磁化率が何かの拡散により経時変化を起こす現象と考えられており、熱揺らぎ磁気余効とは少し違うかもしれません。
Mnフェライトの場合空格子とFeイオンの移動が関係しており、「空格子を少なくすればディスアコモデーションを減らすことができるだろう」(太田 p.329)と書かれています。
より高温の成分(図8.2-3のⅣ、Ⅴ)をアニールアウトすることも有効かもしれません。
湿度は上記拡散を変化させるような化学反応が起これば効くかもしれませんが、磁性材料自身を変えることになるのであまりおすすめしません。
注1:これが私の磁気余効に関する研究につながっており、保磁力は熱揺らぎにより時間の対数に比例して減少するというかなり一般的な議論が可能になります。近角先生の「強磁性体の物理(下)」p.310には「ΔI - log t のグラフの傾斜は温度Tに比例することになる」と書かれていますが、実際にはほとんどの磁気余効でTとの比例関係は見られません。そのことを応用磁気学会で近角先生にお話ししたところ、「Physics of Ferromagnetism の second edition では私の論文を引用するとともにその箇所(p.548)の記述を訂正した」、とのお手紙を先生からいただきました。残念ながらこの訂正は日本語版には適用されないままになってしまいました。
-------------------------------------------------------------------------------------------------
Date: Thu, 3 Mar 2022 05:50:40
AA: 佐藤勝昭様, Oです。 お世話になります。
早速ご丁寧かつ詳細な解説をありがとうございます。
わざわざ調査もしていただき、大変お手数おかけいたしました。文献まで頂戴して感謝いたします。
緩和時間の長いディスアコモデーションもあること、空格子を減らすとDAを減らすことができるであろうこと、そのためにアニールアウトが有効と考えられる事、を理解しました。
以上、宜しくお願い申し上げます。
----------------------------------------------------------------------------------------------------------------------------------------------
1404.ペルチエ素子について
Date: Sat, 5 Mar 2022 17:53:27Q1: 佐藤勝昭 先生
初めまして。
W大学部3年のM*といいます。電子工学について自習していたところモヤモヤしてる部分があり、 ホームページをお見掛けしてご教示していただきたいと思いメールさせてもらいました。
※すみませんがHPに載せる際は匿名でお願いいたします。
一般的なΠ型ペルチェ素子について調べてみると、幅が数cmサイズの大きな物ばかり画像で見つかります。
中のp型, n型の半導体柱も数mm単位の太さのようですが、半導体柱はある程度太くないといけないのでしょうか?
もっと半導体柱を数μmレベルに微細化させれば小型の電子機器にも搭載できるようになり、 単位面積当たりで作成できる素子数が増えて冷却効果が上がるのではと疑問に思いました。
1対のp, n半導体柱の断面積をSとすれば、100対あるペルチェ素子の半導体断面積は100Sになります。(A)
1対当たりの断面積を半分のS/2にすれば、直列で200対も並べられて断面積は100Sになります。(B)
この場合、同じサイズでも(B)の方が素子の数が多いので冷却効率が良くなりそうなのですが、 半導体の断面積が減ると配線抵抗が上がって駆動に問題があるからペルチェ素子は大きくなってしまうのでしょうか?
それならばとても太い断面積100Sの半導体柱を1対置くだけでも大きな冷却能力を得られ大量に直列接続する必要も無いように思います。
また小型の電子機器にもし搭載する場合もその中で発熱する部品の面積がSだとしたら、 発熱箇所も小さいのでその部品の上部に断面積S程度の小さなペルチェ素子を設置するだけでも冷却効果はありそうに思います。
--------------------------------
(1)p, n半導体柱が数mm単位とそれなりに太くないといけない理由は何か
(もし冷却したい対象が小さければペルチェ素子も小型でも問題ないのではないか)
(2)たとえば1本の半導体柱が10mm角サイズの素子と1mm角サイズしかない素子だと駆動電圧は具体的にそれぞれどれぐらいなのか
(一般的なペルチェ素子で必要な駆動電圧(駆動電流の方が正しい?)の何倍なのか)
(3)そもそもペルチェ素子が何対も直列接続しないといけない理由は何か
(直列接続が必要なら何でもっと半導体をもっと微細化しないのか、微細化が出来ないのなら大きな1対のままでもいいのではないか)
--------------------------------------------------------------------------------------------------------------------------------
Date: Sun, 6 Mar 2022 08:42:01 +0900
A1: M君、佐藤勝昭です。
3年生なのに自分で考えて質問するのは偉いですね。
(1)p, n半導体柱が数mm単位とそれなりに太くないといけない理由は何か (もし冷却したい対象が小さければペルチェ素子も小型でも問題ないのではないか)
キャリアによって輸送されるエネルギー束(単位時間・単位面積あたり運ばれるエネルギー)Φは電流密度Jに比例し、Φ=πJで表されます。πはペルチエ係数。 (A1)あなたの言うとおり、冷却対象が小さければ、面積が小さいので、細くてもOKです。 冷却対象が大きいと、電流密度には限界があるので面積で稼がなくてはなりません。
(2)たとえば1本の半導体柱が10mm角サイズの素子と1mm角サイズしかない素子だと駆動電圧は具体的にそれぞれどれぐらいなのか(一般的なペルチェ素子で必要な駆動電圧( 駆動電流の方が正しい?)の何倍なのか)
(3)そもそもペルチェ素子が何対も直列接続しないといけない理由は何か(直列接続が必要なら何でもっと半導体をもっと微細化しないのか、微細化が出来ないのなら大きな 1対のままでもいいのではないか)
(A2,3) ★決してナノサイズの熱電素子が研究されていないわけではありません。早稲田大学では、シリコンナノワイヤを使った 微小熱電素子(センサ)が研究されています。
また、
★なお、ナノサイズになると、フォノンの散乱が大きくなって熱伝導率が悪くなって 熱電性能指数が高くなるので、それをペルチエ素子に使うという研究開発もあります。
--------------------------------------------------------------------------------------------------------------------------------
Date: Sun, 6 Mar 2022 22:32:35
Q2: Mです。1日で返信をいただけて嬉しいです。
(1)輸送されるエネルギー束Φ=πJというのは移動する熱エネルギーだと思いますが、電流密度Jがどんなに小さくても一応熱の移動自体は起こるのですか?
半導体の接合が関連するのでバンドギャップを超えるだけのエネルギーに相当する電圧、ダイオードでいう閾値以上の電圧がないと熱の移動は起きないのだと思っていました。
またペルチェ係数は既知として、どれぐらいの電流密度があれば何℃冷却されるかを考える場合は、Φ=πJの式からどのように式変形して求まりますか?
温度変化として具体的なイメージを掴みたいです。
(2), (3)熱電性能指数Zの分母にある熱伝導度κが下がるとZが良くなるという意味だと思いますがこれはゼーベック効果の事であって、 ペルチェ効果だとκが小さくなるとペルチェ係数πも小さくなってエネルギー束Φが小さくなったりしないのですか?
再度、質問に回答をいただける幸いです。よろしくお願いいたします。
----------------------------------------------------------------------------------------------------------------------------------
Date: Tue, 15 Mar 2022 06:39:16
A2: M君、佐藤勝昭です。 再度のご質問への回答が遅くなってごめんなさい。実は、私自身は熱電効果は素人なので、熱電素子に詳しいNIMS(物質材料研究機構)の内田健一博士(スピンゼーベック効果の発見者)にお問い合わせしていました。 このたび、回答をいただきましたので、以下に紹介します。参考にしてください。
-------------------------------------------------------------
ペルチェ効果のみならず、熱電半導体に電流を流すと発生するジュール熱も考える必要があります。ペルチェ効果による吸発熱は電流に比例、ジュール熱は電流の2乗に比例 ですので、どんなペルチェ素子であっても電流を流し過ぎるとジュール熱に負けて冷却できなくなります。
最初のご質問「p, n半導体柱が数mm単位とそれなりに太くないといけない理由は何か」に関しては、
A:半導体柱が大きな1個だけの場合: 現実的な電流源で電流を流しても電流密度が小さ過ぎて大きな温度変化が生じない
半導体柱を非常に細かくたくさん繋げた場合: 電流密度が高くなりすぎてジュール熱に負けて冷却できない
となります。
市販の多くのペルチェ素子は典型的な電流源のスペックに合わせて数A程度で大きな冷却効果が得られるように設計してあり、それが結果として柱1本あたり1mm程度のオーダーになります。
(1)電流密度Jがどんなに小さくても一応熱の移動自体は起こるのですか?
A:熱電効果は線形応答現象であり、熱電素子は基本的にオーミック接触になっていますので、起こります。
(2)またペルチェ係数は既知として、どれぐらいの電流密度があれば何℃冷却されるかを考える場合は、Φ=πJの式からどのように式変形して求まりますか?
A:ペルチェ係数の性能(成績係数COP)は多くの教科書に詳しく導出が載っています。ペルチェ熱だけでなくジュール熱(より詳細に扱う場合はトムソン熱も)を考慮して計算されます。
例えば名古屋大学・寺崎先生の「熱電材料の物質科学」にコンパクトに解説されています。
ペルチェ効果の性能もκが小さくなると上がり、ゼーベック効果と同じく性能指数ZTが良いほど良いです。ペルチェ係数πとゼーベック係数Sの間には相反関係(π=ST)が成り立ちますので、良いゼーベック材料=良いペルチェ材料です。
半導体では熱伝導は半導体が担い、ペルチェ係数は伝導電子/ホールが担いますので、πとκはほぼ独立変数です。金属の場合はκと電気伝導率σには正の相関があり、σ(とκ)が大きいほどSが小さくなる傾向にあるので、κが大きな金属はペルチェ材料にはなりません。
------------------------------------------------------------------------------------------------------------------------------
Date: Wed, 16 Mar 2022 21:44:31
AA: 佐藤勝昭先生, Mです。
ご丁寧に専門家へお問い合わせまでしてくださりありがとうございました。
簡潔で明快なご説明でスッキリし、大変勉強になりました。
お忙しい中にもかかわらず佐藤勝昭先生、並びに内田健一先生、ご回答ありがとうございました。
------------------------------------------------------------------------------------------------------------------------------
1405.干渉膜の反射減衰量について
Date: 2022/03/08 10:40Q: 佐藤勝昭 様
初めてメール差し上げております。T社のOと申します。よろしくお願い申し上げます。
先生のホームページは以前より拝見致しておりまして、教科書や他のホームページでは詳しく解説されていない(探し当てられない)ことを、ピンポイントで説明頂けているので、大変参考になります。
今回ですが、先生のご回答済み項目「1402.非反射膜の干渉について」は、私も同様の疑問を持っていたので、目から鱗が落ちたように明解で、非常に参考になりました。
それで、この関連の質問になりますが、「表面反射光(入射光)と裏面反射光が互いに干渉して弱めあって消滅する」で、それぞれの光量(波の高さ)はどう作用するのでしょうか。
レンズのような透過基板や、太陽電池のような吸収基板ではなく、金属の反射基板上に、1/4λ干渉膜をコーティングした場合にどうなるかということです。
コーティング膜での表面反射が半分以上の場合は当然、反射光が観測されると思いますが、入射量の方が多い場合は、基板からの裏面反射と膜表面反射の差分が反射光として観測されるということでよろしいでしょうか。 それとも、全ての裏面反射光が入射光に押し戻されて膜外に出られず膜内でエネルギー散逸することになるのでしょうか。
可視光では、非常に強い吸光度を持つ材料が多々ありますので、わざわざ上記のようなことをする意味がないかと思いますが、GHz~THzレベルの電磁波では1パスの透過吸収が難しいため、有効な手法になるかと思い、確認の質問をしております。
---------------------------------------------------------------------------------------------------------------------------------
Date: Wed, 16 Mar 2022 09:33:22
A: O様、佐藤勝昭です。 お返事が遅くなり申し訳ありません。
空気/薄膜/基板の反射率の計算については、「物性なんでもQ&A」の#108にあります。
ご質問は、基板が金属の場合でしたね。例えば、空気/MgF2薄膜/アルミニウムについて#108の式で計算してみましょう。
波長550nmとしますと、空気の屈折率nは1, MgF2の屈折率nは1.37, Alの屈折率,消光係数葉、n=0.82,k=5.99を使って、
空気/薄膜の振幅反射率r0=-0.156,
薄膜/基板の複素振幅反射率r1=0.833-i0.403
となり、空気/MgF2薄膜/アルミニウムの複素振幅反射率rは,Φ=π/2として
r=(r0-r1)/(1-r1r0)
光のエネルギー反射率は複素振幅反射率の絶対値の二乗なので
R=|r|^2=rr*=0.819
金属への透過率はT=1-R=0.181
入射光の18.1%は金属の中に光が入って金属に吸収されます。
一方、空気/アルミニウムのエネルギー反射率は
R=0.916
薄膜を使わないとき91.6%のAlの反射率が、1/4波長厚のMgF2薄膜を入れると81.9%に減少しています。
----------------------
ご質問は入射光と反射光を別々に考えていますが、膜の中では、波の多重反射干渉なので、押し戻されたりするのではなく両者を一体として考えなくてはなりません。
膜の消光係数は0なので、エネルギーの散逸はあくまで裏面の金属の中で起きます。
-------------------------
ご質問では、GHz~THzの電磁波に言及されていますが、この場合は、メタマテリアル、メタサーフェスなどを用いて反射の制御を行うことができます。
--------------------------------------------------------------------------------------------------------------------------------
Date: Wed, 16 Mar 2022 11:29:11
AA: 佐藤勝昭先生
T社のOです。
ご多用のところご回答頂きましてありがとうございました。既に同種のQ&Aがあったとのことで、お手数をお掛け致しまして恐縮です。
ご指摘頂いた通り、最初の視点が違っていたので、探し当てることも、理解も難しかったのですね。
最初にも申しましたが、数式の展開・解釈には疎いので、詳細なところはこれからじっくり拝見、検証致しますが、要は、波の(一往復ではなく)多重反射干渉が重要ということと、基板からの反射を(金属だからほぼ)100%で考えるのではなく、屈折率、消光係数をきちんと考慮する(時により薄膜の値より寄与が大きい)ということですね。
大変参考になるご回答頂きましてありがとうございました、今後ともよろしくお願い申し上げます。
---------------------------------------------------------------------------------------------------------------------------------
1406.775nm厚のシリコンの反射率について
Date: Mon, 21 Mar 2022 08:39:53Q: 物性なんでもQ&Aを拝見しまして、連絡いたしました。とても充実したHPを作成いただき、感謝しております。どうもありがとうございます。
私はD*社に勤務するM*と申します。匿名希望で所属も未公開でお願いいたします。
QandAを「反射率」のキーワード検索で辿りましたが、本質問の内容とおなじものがなさそうなので、質問いたしました。
(また自分でいろいろ考えてみましたが、何を見落としているかわかりませんでしたので。。。)
質問内容は、「775um厚と厚いシリコンの裏面反射を含む反射率の波長依存性を計算で算出するにはどうしたらいいか。」というものです。
背景は下記となります。
1. 空気中の775um厚のシリコンの反射率の波長依存性(900-1500nm)を計算したのですが、実験結果を再現できませんでした。
 添付(私の計算結果)のように反射率0%と約70%の間を振動しています。
添付(私の計算結果)のように反射率0%と約70%の間を振動しています。位相が強め合うときと位相が弱め合うときに対応しているのかと考えますが、実験結果は添付(正しいと思われる結果)のようになります。
2. 多層膜の反射率の式を用いて計算しています。(数百nmの膜がSi上にある状況であれば、実験結果が再現できています。)
Er=E0r0+E0(1-r02)r1exp(i2φ){1-r1r0exp(i2φ)+(-r1r0)2exp(i4φ)+・・}
=E0r0+E0(1-r02)r1exp(i2φ)/{1+r1r0exp(i2φ)}
=E0{r0+r1exp(i2φ)}/{1+r1r0exp(i2φ)}
3. FILMETRICSのサイトの計算からは実験結果を再現できています。(画像も添付させていただきました。)
波長1000nm以下ではほとんど表面反射の効果しかなく、1050nmから反射率が立ち上がっていくのがなぜか理解できていません。
波長が変わると重ね合わさるときの位相が変わると思うのですが、反射率の振動幅は変わらないと思い、結果に違和感を感じています。
しかし、実験結果と一致していますし、お手上げという状況です。
一つの予想として、コヒーレンス長<膜厚となったから、上記式が一部成り立たなくなったというものがあるのですが、どのように修正すれば、実験結果を再現できるかはわからず。。。
以上、ながながと書いてしまいましたが、ご回答いただければ幸いです。
----------------------------------------------------------------------------------------------------------------------------------
Date: Mon, 21 Mar 2022 09:25:52
A1: Mさま、佐藤勝昭です。
φを計算するのにシリコンの屈折率、消光係数のスペクトルデータは、何をお使いでしょうか?
あなたの計算結果を見ると吸収端より短波長でも干渉縞が出ているので、吸収(消光係数)が考慮されていないと思います。
例えば、波長900nmにおける吸収係数はα=700cm^-1なのでd=7.75x10-4m=7.75x10-2cmなので、 αd=54.25 従ってexp(-54.25)=2.25x10^-24
となって、光は裏まで到達しないはずで、干渉縞が起きるはずがありません。
----------------------------------------------------------------------------------------------------------------------------------
Date: Mon, 21 Mar 2022 10:21:37
Q2: 佐藤様
早速のご返信をどうもありがとうございます。
シリコンの屈折率は3.55で固定、消衰係数は0で計算しておりました。
消衰係数は小さいので0にしてしまっていましたが、そういえば、侵入深さに換算すると無視できないことを最近計算したばかりでした。。。ご指摘どうもありがとうございます!
そして
・波長900nmでは表面反射のみ考えた値とほとんど一致している
→裏面反射がなくなった。→理由は?→減衰 と予想するべきでした。
消衰係数を考えることで、定性的には1050nm以降の急峻な立ち上がりは吸収がなくなるためとわかりました。
定量的には、
・消衰係数の効果は振幅の減衰なので、反射率の式においてexp[i2φ]をexp[-α dcosθ] exp[i2φ]に変更すればよい。
と考えました。
ひとまず、これで再度計算してみます。
もし間違っていましたら、ご連絡いただけると幸いです。
以上、どうぞよろしくお願いいたします。
-----------------------------------------------------------------------------------------------------------------------------------
Date: Mon, 21 Mar 2022 15:38:28
A2: Mさま
吸収係数は、波長とともに大きく変化します。
n,kの波長毎のデータを使わないとだめです。
また、消光係数kと吸収英数αの関係は
gallery.com/education/el/slide_hikari02.pdf
のp13を参考にしてください。
添付は、Palik:Optical Constants of Solidsのp561-p566のコピーです。
φ=2π(n+ik)d/λ
exp(i2φ)=exp(-4πkd/λ)exp(i4πnd/λ)
となります。この式のn,kに添付の波長λ毎の数値をいれて計算してください。
------------------------------------------------------------------------------------------------------------------------------------
Date: Mon, 21 Mar 2022 16:17:45
Q3: 佐藤様
ご連絡をどうもありがとうございます。
減衰をいれることで定性的に結果を再現することができました。
 添付のグラフです。
添付のグラフです。しかし、複素屈折率の良いデータを持っていなかったので、FILMETRICSのサイトから 持ってきたものの値が歯抜けでこまっておりました。
添付のグラフがなめらかでなく、本来の依存性と異なるのはn, kが正しくない値だからのはずです。
いただいたデータがあれば、より詳細な計算ができそうです。どうもありがとうございます。
(Palikは学生時代もお世話になりました。なつかしいです。)
また干渉ありなしの両方で計算したところ775umの膜厚になると干渉を考えない(位相差を考えない)強度のみの足し算で実験結果を説明できそうなことがわかってきました。
逆に位相差をいれると私の計算では、振動が見えてしまって実験結果とずれてしまいます。
本当は両者が一致するはずと思うのですが、私の式だと何か間違っているようです。
Er=E0r0+E0(1-r02)r1exp(i2φ){1-r1r0exp(i2φ)+(-r1r0)2exp(i4φ)+・・}
=E0r0+E0(1-r02)r1exp(i2φ)/{1+r1r0exp(i2φ)}
=E0{r0+r1exp(i2φ)}/{1+r1r0exp(i2φ)}
の式で再現できるはずですよね?
先ほども共有したFILMETERICSのサイトでは、きざみを0.1nmにすると振動しているのが見えて、きざみを1nmにすると振動が見えなくなります。干渉を考えた式で計算している証拠だと思っています。
このサイトがどう計算しているのかが不思議です。 -------------------------------------------------------------------------------------------------------------------------------------
Date: Mon, 21 Mar 2022 17:50:14
A3: Mさま、佐藤勝昭です。
Palikのデータも吸収端付近は歯抜けですね。
式は間違っていませんが、複素数の計算は結構面倒ですよ。
また最終的にはR=|r|^2=rr*を計算しなくてはなりません。
物性なんでもQ&A #109.コメント「エクセルで薄膜の反射率が計算できる」を参考にしてください。
--------------------------------------------------------------------------------------------------------------------------------------
1407.酸化皮膜の色について
Date: Tue, 5 Jul 2022 07:37:05Q1: 佐藤様、お世話になります。Y*社のY*です。
HPを拝見して質問させていただきます。なお、Webにアップする際は、匿名を希望します。
具体的な質問は以下の通りです。
ステンレスやチタンは、その表面の酸化皮膜の厚さによって、さまざまな色調を呈することが知られており、これらは干渉色と言われています。
ある金属を表面処理して表面に酸化物を形成させた場合、特定の色調を呈しているのですが、その発色原理が干渉色によるものか、その酸化皮膜自体の色なのかを調べたいと思っています。
この皮膜が色調と呈している原理が、酸化皮膜自体の色か、干渉色かを調査する手法、あるいはステンレスやチタンの発色が干渉色であることを証明する手法についてお教えいただけないでしょうか?
お手数をおかけしますが、ご回答いただければ幸いです。
どうぞよろしくお願いします。
---------------------------------------------------------------------------------------------------------------------------------------
Date: Tue, 5 Jul 2022 22:32:43
A1: Yさま、佐藤勝昭です。
干渉色か固有の色かはスペクトルを測定すれば分かります。
干渉色の場合、酸化膜の膜厚に応じて、スペクトル(干渉縞)の間隔が変化しますが、固有色の場合、膜厚によってピークあるいは吸収端の波長は変化しません。
----------------------------------------------------------------------------------------------------------------------------------------
Date: Wed, 6 Jul 2022 02:18:33
Q2: 佐藤様
お世話になります。早速ご回答いただきありがとうございました。
ご回答いただいた内容について、もう少しお聞かせいただけないでしょうか?
干渉色の場合、酸化膜の膜厚に応じて、スペクトル(干渉縞)の間隔が変化します
「酸化膜の膜厚に応じて」ということは、例えば、ステンレスの酸化皮膜で例えると、下図のように、ブルーの色を呈する約0.16μmの皮膜と、グリーンの色を呈する約0.27μmの皮膜で、スペクトルの間隔が変化するという意味でしょうか?
 (Intovent | 事業紹介 | 株式会社田中商店のHPによる)
(Intovent | 事業紹介 | 株式会社田中商店のHPによる)それとも、ブルーの色を呈する約0.16μm前後の皮膜範囲内で、スペクトルの間隔が変化するという意味でしょうか?
今回調べたいと思っている酸化皮膜は、おおよそ20nmから80mnくらいの厚みで、これ以上、皮膜厚さを変化さえることが難しいため、 おおよそ20nmから80mnくらいの厚みの皮膜自体が、干渉色によるものか、その酸化皮膜自体の色なのかを調べられないかと思っています。
お手数ですが、アドバイス頂けると幸いです。
どうぞよろしくお願いします。
----------------------------------------------------------------------------------------------------------------------------------------
Date: Wed, 6 Jul 2022 14:34:51
A2: Yさま、佐藤勝昭です。
光路差が光の波長λの整数倍であれば、干渉は強め合い、半整数倍なら弱め合います。
(詳細はWikipedia参照)
光の干渉で、強める条件は直入射の場合2nd=mλ (dは膜厚、λは波長、mは整数)です。
仮に不動態膜の屈折率をn=3とします。(Cr2O3で2.55, Fe3O4で2.4)
d=160nmならmλ=2nd=960 なので、m=1のとき960nm(赤外), m=2のとき480nm(青)付近で強く青に着色します。
d=270nmならmλ=1620, m=1では1620nm(赤外), m=2で810nm(赤外),m=3では540nm(緑)で強く緑に着色します。
もし、20nmから80nmの厚みだと2nd=120nm~480nmなので、かろうじて80nmの膜で青く着色しますが20nmでは干渉色はつきません。
20nmで着色しているとすれば、膜そのものの色でしょう。
-----------------------------------------------------------------------------------------------------------------------------------------
Date: Wed, 6 Jul 2022 06:22:54
AA: 佐藤様、お世話になります。早速ご返答いただきありがとうございました。
よく理解できました。
-----------------------------------------------------------------------------------------------------------------------------------------
1408.誘電率と誘電正接の関係について
Date: Sun, 18 Sep 2022 06:37:26Q: 佐藤勝昭 先生、初めてメールさせていただきます。
M*社で樹脂開発に従事しておりますK*と申します。
学生のころから20年くらい、先生のHPを楽しく拝見させていただいております。
近年、高周波通信の需要から、GHz以上の周波数領域で低誘電率・低誘電正接の樹脂材料が求められており、弊社も精力的に開発を進めております。
分子構造から誘電正接を予測する理論はまだ確立されていないと理解しておりますが、当該分野の実験系の文献では、誘電率を低く(すなわち局所局所の分極を小さく)なるよう設計すれば、誘電正接も低くなるであろうという論調が多く見られます。
他方、誘電正接の定義はtanδ=ε"/ε'と、誘電率が大きい方が小さくなる理解です。
直感的には分極が小さい方が分極反転の影響も受けにくい、というのはわかるのですが、それがどうしてε"を小さくすることに結び付くか、理論・定式があるかなどのご知見はございますでしょうか.
お忙しいところ恐縮ですが、ご教示いただけますと幸いです。
------------------------------------------------------------------------------------------------------------------------------------------
Date: Sun, 18 Sep 2022 17:03:30
A: K様、佐藤勝昭です。
メールありがとうございます。
「誘電率を低く(すなわち局所局所の分極を小さく)なるよう設計すれば、誘電正接も低くなるであろうという論調」については存じ上げません。
ご指摘のように、誘電正接=ε"/ε'なので、誘電損失を表すε"を小さくしなければなりません。
0.1GHz以下では、配向分極が追従できなくなることが誘電損失の原因ですが、10GHzから1THzの周波数帯では分子運動の緩和によって決まるので結晶の場合は欠陥が少ない材料、非晶質では不純物の少ない材料が 開発の目標となります。
===============================参考===================================
私は、JST-CRDSの特任フェローとして2021年度に発表した戦略プロポーザル「無線・光融合基盤技術の研究開発~次世代通信技術の高度化に向けて~」(CRDS-FY2021-SP07)を策定するチームに加わり、100GHzに向けた誘電材料の開発について担当しました。以下には、その部分を引用します。
(高周波用低損失基板材料)
周波数が高くなってくると、配線や基板なども分布定数回路の一部として扱う必要があるとともに、金属の表皮効果が顕著になって導体損失が増え(周波数の平方根に比例して電気抵抗が増加)、絶縁基板の誘電損失も増加する。このため、導体損失や誘電損失の少ない(誘電正接が低い)材料の探索が重要になる。また、金属導体と絶縁基板との界面の凹凸が導体損失を増大させるため、例えば0.1THzでは界面の凹凸をサブミクロンレベルまで低減させることが望まれ、界面の接着性を保ちながら導体損失を抑える導体形成技術(加工・成膜プロセス技術、高平滑に金属と誘電体を接合する表面処理技術など)への挑戦が期待される。
絶縁基板材料としては、伝送損失を減らすために誘電正接が低い有機高分子材料(例えばポリフェニレンエーテル(PPE)樹脂、ポリテトラフルオロエチレン(PTFE)樹脂)が用いられている。高分子材料の1GHz以下の周波数での誘電損失は、分極が高周波に追従できなくなるために誘電正接(tanδ)が生じることによるが、10GHzから1THzの周波数帯での誘電損失は結晶域内の格子振動や非晶域内の分子鎖の運動に起因する吸収で生じるため、これらの低減が重要となる。研究開発の一例としては、不純物や結晶欠陥などを減らすことで誘電損失を下げる試みが行われている。
(出典:富川真佐夫:工業材料69巻5号p.54, 中川幸一:高分子27巻2号p.97)
参考になれば幸いです。
-------------------------------------------------------------------------------------------------------------------------------------------
Date: Mon, 19 Sep 2022 00:21:24
AA: 佐藤先生、お世話になっております、M社Kです。
早速のご回答、どうもありがとうございました。大変参考になりました。
JST-CRDSの件も、教えていただきありがとうございました。佐藤先生がそのような取り組みをされていること、寡聞にして存じ上げませんでした。
-------------------------------------------------------------------------------------------------------------------------------------------
1409.アルミニウムの酸化皮膜が干渉色を示さない理由について
Date: Thu, 6 Oct 2022 07:32:25Q: 佐藤先生、お世話になります。Y社のYです。
以前に酸化皮膜の色についてお教えいただき、ありがとうございました。
今回は別件となりますが、お教えいただきたいことがあります。
一般的にアルミニウムは陽極酸化処理により人工的な酸化皮膜を成長させることが知られており、染料により加飾されていますが、 アルミニウムの酸化皮膜で、ステンレスやチタンのように酸化皮膜の厚さのみで干渉色を発生させることができないのでしょうか?
アルミニウムの酸化皮膜が干渉色を示さない原理など、ご指導いただければと思っております。
お忙しい中恐縮ですが、どうぞよろしくお願いします。
なお、Webにアップする際は、匿名を希望します。
-------------------------------------------------------------------------------------------------------------------------------------------
Date: Thu, 6 Oct 2022 19:02:42
A: Y様、佐藤勝昭です。
酸化アルミニウムの屈折率は1.6(@700nm)と小さいので2nd=mλの式を考慮すると、n=3の場合の2倍の厚さが必要になります。
アルミニウムの自然酸化膜は10Å程度の薄さなので、干渉縞は生じません。
陽極酸化によって作った酸化アルミニウムは多孔質アルミニウムとなり表面はでこぼこで平坦性が悪いため光の散乱が起きて干渉縞が出にくいと思われます。
ALDのように丁寧に作れば、干渉縞の出るような平坦な膜ができます。
例えば、特許「複雑腕時計コンポーネントのための保護コーティング」には、次のように書かれています。
「ALD法及び反応機構の原理及び利点はこの文献に詳細に説明されている。
特に、この技術によって単分子層を生成することができ、それによって非常に制御されたコーティングの成長が可能となる。数層の層を互いの上部に堆積させた場合、事実上ピンホールや欠陥のない非常に密なコーティングを得ることができる。ALD層は、この文献によれば、腕時計産業において装飾の目的で適用される。特に、堆積される層の性質及び膜厚に特有の新しい色を呈するであろう反射基材上に、ALDによって例えばアルミナ製の薄い透明層を堆積させることにより、干渉色を得る ことができることが報告されている。」
--------------------------------------------------------------------------------------------------------------------------------------------
Date: Wed, 12 Oct 2022 04:08:29
AA: 佐藤様、お世話になります。Y社のY社です。早速ありがとうございました。
理解できました。
--------------------------------------------------------------------------------------------------------------------------------------------
1410.ラマン散乱の半値幅と分子運動の緩和時間の関係式について
Date:Thu, 9 Feb 2023 22:05:47Q1: 初めてメールする元C社勤務のK*(匿名希望)です。
ラマン散乱に関するページを拝見しました。
大学生当時、液体の分子運動について、ラマン散乱を用いて、研究していました。分子振動の緩和時間を計算するために 「物理化学実験 ラマンスペクトル」のp7に書かれている
「MX4 型分子の場合,全対称伸縮振動ν1 ピークの半値全幅Δν1佐藤は分子の振動緩和時間τV つまり振動が減 衰するまでの寿命と次のような関係がある。
τV =1/πcΔνν1 (17)
一方,配向緩和時間τR(分子の向きが反転するのに要する時間に比例する)は,変角振動(ν2,ν4)ピークの半値幅から次式により求めることができる。
τR =1/{πc (Δν2or4 − Δν1)} (18)」
という式で、半値幅から、緩和時間を計算していました。代々この式を使っていましたが、出典を知りません。
成著等あれば、知りたいです。
------------------------------------------------------------------------------------------------------------------------------------------
Date: Thu, 9 Feb 2023 22:56:41 +0900
A1: K様、佐藤勝昭です。
いま、手元にないので自信がありませんが、ラマン分光については、浜口宏夫,平川暁子編「ラマン分光法」(日本分光学会)学会出版センター 1988. に詳しく載っているのではないかと思うのですが・・
私の「基礎から学ぶ光物性・補足試料:ラマン分光と赤外分光」のスライドを作ったときは、当時勤めていた農工大の図書館で借りた浜口先生の「ラマン分光法」 を参照しました。
-------------------------------------------------------------------------------------------------------------------------------------------
Date: Fri, 10 Feb 2023 05:16:22
Q2: 佐藤様、お世話になります。
ご返信ありがとうございます。
卒論作成時に精読した際の記憶では、浜口宏夫,平川暁子編「ラマン分光法」には記載ないはずです。
スペクトル幅の解析は、ラマン効果とは別の話題のようです。代々の論文記載以外に、見当たらないのです。
先のメールのリンク先が、珍しい限りです。
お気分悪くされましたら、陳謝します。
-------------------------------------------------------------------------------------------------------------------------------------------
Date: Fri, 10 Feb 2023 16:52:57 A2: K様、佐藤勝昭です。 そうですか、浜口先生の本には載っていないのですね。
引用された「物理化学実験 ラマンスペクトル」のpdfは、山形大学理学部の天羽優子准教授の公式ホームページに掲載されたものです。
天羽先生は、低振動数ラマンの研究で科研費に採択されています。
(科研費基盤C「超臨界アルコールのラマン散乱:分子間ダイナミクスの古典性と量子性」)
おそらく、あの式は、先生自身の論文に掲載されたものだと思います。
山形大のHPによると天羽先生のメールアドレスはapj@cm.kj.yamagata-u.ac.jpとなっています。 天羽先生に、直接コンタクトされてはいかがですか。
--------------------------------------------------------------------------------------------------------------------------------------------
Date: Sat, 11 Feb 2023 02:36:07
Q3: 佐藤様、お世話になります。
ご返信ありがとうございます。参考とさせていただきます。
当方、卒論の頃、研究室の歴代卒業生が本式を皆使うものの、出典不明であることを記憶しています。
ラマンでこのようなアプローチするのは、レアなのでしょうか。
何かお気づきのことあれば、ご教示ください。
--------------------------------------------------------------------------------------------------------------------------------------------
Date: Sat, 11 Feb 2023 22:23:39
A3: K様、佐藤勝昭です。
ネットサーフィンで調べたところ、分子の低振動数ラマンスペクトルによる緩和現象 は天羽優子先生とお茶の水大の富永靖徳先生の共著論文が多数あることがわかりました。
K様の質問に関係ありそうなのは次の論文です。
(http://www.cml-office.org/atom11archive/lab2/papers.html による)
Y.Amo and Y.Tominaga, "Low-frequency Raman scattering of liquid CCl4, CHCl3 and acetone", J. Chem. Phys. 109 (1998) 3994-3998
この論文の概要は
「代表的な有機溶媒である四塩化炭素、クロロホルム、アセトンの低振動数ラマンスペクトルに現れる、緩和型のモードは、従来のCole-Cole型の緩和関数では全く説明がで きない。そこで、二状態遷移モデルに基づいた、Multiple Random Telegraph (MRT)モデルの緩和関数を用いて説明することを世界で初めて試みた。四塩化炭素とアセトンで は、十分に満足のいく結果が得られ、MRTモデルによる緩和の解析の妥当性が示された。クロロホルムにおけるわずかなずれは、ガウス型のモードを一個導入することにより 解決される。」と書かれています。
また、解説論文としては
天羽優子、冨永靖徳、「低振動数ラマン散乱でみる液体の緩和と振動」, 日本物理学会誌 55 3(2000) 205-208.
概要は「2状態遷移模型に基づく緩和関数を用いて、液体の低振動数ラマン散乱のスペクトルを解析した。THz領域に現れる、分子間相互作用による緩和モードでは、overdamped limitとnarrowing limitの両方の破れを考慮することが不可欠である。特に、揺らぎの相関久保数と物性がちゃんと結びついている点が大事である。」と書かれています。
--------------------------------------------------------------------------------------------------------------------------------------------
Date: Sun, 12 Feb 2023 22:22:55
AA: 佐藤様
お世話になります。丁寧なご返信ありがとうございます。
参考とさせていただきます。
冨永先生ですが、卒論で読んだ「溶液の分子論的描像」にて、共同執筆されています。
北大の井川先生が、くだんの式について本書で触れていました。
出典記載はなく、自明の印象を受けました。初学者には、厳しい話ですが・・・。
--------------------------------------------------------------------------------------------------------------------------------------------
1411.シリコンフォトダイオードのサブギャップ光応答について
Date: Fri, 10 Mar 2023 19:47:01Q: 佐藤勝昭様,はじめまして、M社のK*と申します。
"物性なんでもQ&A" 含めた佐藤様のWEBサイト拝見させていただき、勉強させて頂いており、非常にためになっております。大変ありがとうございます。
今回、シリコンフォトダイオードの光検出波長に関して、質問させていただきことがあり、メールさせていただきました。(匿名希望でお願い致します。)
~経緯~
IRカットフィルタがない画像データが出力できる市販のモノクロCMOS(Si)イメージセンサーにSWIR 1,300nm以上の波長光を照射させたところ、画像としてわずかながら照射反応が見られました。
波長としては、1,300nm、1,450nm、1,550nmで確認し、光源としてはシングルモードのレーザーダイオードを使用して、外光が入射されない環境で照射しています。
シングルモードのレーザーダイオードを使用しており、1,100nm以下の波長もほとんど含まれない認識です。
バンドギャップエネルギー 1.12eVのSi(シリコン)で製作されたCMOSイメージセンサ(=シリコンフォトダイオード)では、およそ1,100nm以上の波長に関して検出されない認識で、 1,100nm以上の波長を検出するにはシリコンではなくバンドギャップエネルギーが小さいInGaAsなどを使ったフォトダイオードを使うしかないと思っていました。
~質問~
シリコンで製作されたイメージセンサで、1,100nm以上の波長が検出できる要因としてどのような現象が考えられますでしょうか?
物性なんでもQ&A:144.半導体のサブギャップ吸収 で説明されていました吸収要因で内部光電効果を発生することによりイメージセンサとしても1,100nm以上の光を検出していると考えて良いのでしょうか?
何卒、ご回答のほど、よろしくお願いいたします。
------------------------------------------------------------------------------------------------------------------------------------------
Date: Fri, 10 Mar 2023 23:09:03
A1: K様、佐藤勝昭です。
お察しのように、サブギャップのバンドー不純物準位間遷移による吸収による光電効果だと思います。
なお、強いレーザー光で励起した場合、二光子吸収によってバンド間遷移が起きる場合があります。
この場合は、レーザー強度を変化したときに強度の2乗で変化するので見分けることができます。
サブバンドギャップ赤外光用のシリコンフォトダイオードについては、
・Chao Li, et al.; Infrared absorption and sub-bandgap photo-response of hyperdoped silicon by ion implantation and ultrafast laser melting, Journal of Alloys and Compounds Volume 883, 25 November 2021,
・Maurizio Casalino et al.: Near-Infrared Sub-Bandgap All-Silicon Photodetectors: State of the Art and Perspectives, Sensors 2010, 10(12), 10571-10600.
が参考になります。
-------------------------------------------------------------------------------------------------------------------------------------------
Date: Sat, 11 Mar 2023 09:26:54
A2: 追伸、K様、佐藤勝昭です。
中赤外光用のシリコンフォトダイオードについて
Richard R. Grote et al.: Extrinsic photodiodes for integrated mid-infrared silicon photonics; Optica Vol. 1, Issue 4, pp. 264-267 (2014)
によれば、Zn+をインプラントしたSi導波路型フォトダイオードが室温で 2.2~2.4μmにおいて 87±29mA/Wの応答、10μA以下の低暗電流を示したとあります。このダイオードの光応答は、 ドーパント起源の価電子帯から0.58eVにあるサブバンドギャップ トラップから伝導帯への遷移によるとされています。
-------------------------------------------------------------------------------------------------------------------------------------------
Date: Mon, 13 Mar 2023 10:22:08
AA: 佐藤勝昭様, M社Kです。お世話になります。
早速のご回答及び追伸まで頂き、ありがとうございます。
一般的なCMOS(ボロンやリン)のドーピングでもサブバンドギャップでの励起を考えると、1,100nm以上の波長も反応することがあると理解しました。
また、二光子吸収の関して現象を知らなかったので、勉強してみます。
非常に貴重な回答いただき、ありがとうございました。
大変感謝しております。
本Q&A、理系・文系問わず物理現象に興味持つものに取って、非常に有益なコンテンツですので、引き続き更新いただけると幸いです。
楽しみに拝見させていただきます。大変ありがとうございました。
-------------------------------------------------------------------------------------------------------------------------------------------
1412.真空環境下での樹脂劣化について
Date: 11 Apr 2023 10:06:30Q1: 佐藤先生、K*社のN*と申します。HPを見て、問い合わせをさせていただきました。
お手数ですが、下記ご回答いただければ幸いです。
※大変恐縮ですが、Webで公開する場合には社名・氏名ともに匿名でお願い致します
真空環境下における樹脂劣化について相談させてください。
〇相談内容
・そもそも樹脂は真空環境下で劣化するものでしょうか?(酸化のリスクがないので劣化懸念は低い?)
※劣化する場合は、メカニズムもご教授いただけると大変参考になります
・真空環境下で使用するのに適した樹脂材料はありますでしょうか?
〇背景
社内設備の真空環境下(温度60℃、真空度10^-3Pa程度)で使用する部品(真空配管やチャンバー)を樹脂化する検討をしており、長期的な寿命観点で懸念がないか検討しています。 よろしくお願いいたします。
-------------------------------------------------------------------------------------------------------------------------------------------
Date: Wed, 12 Apr 2023 12:02:20
A1: N様、佐藤勝昭です。 私は、真空技術の専門家ではありませんので、正確さを欠くかもしれないことをお含み置きください。
Meyer Tool & MfgのPlastics in Vacuum Applicationというサイトによると、一般にプラスチックは、ガス放出性があり、高真空配管や真空容器には向かないとされています。
また、真空配管や真空容器は温度を上げてベーキングをして吸着した水や気体分子を放出しなければなりませんが、テフロンの商品名で知られるポリテトラフルオロエチレン(PTFE)ですら融点が327℃なので260℃以下でしかベーキングできません。ケーブルの絶縁被服材として用いられるカプトンの商品名で知られる超耐熱・超耐寒性ポリイミドフィルムは400℃までの耐熱性がありますが、真空容器の材料としては、用いられません。
吸湿性の少ない材料としては、 ポリエチレン、ポリプロピレン、テフロン (FEP, PTFE, PFA)とポリ塩化ビニル(PVC)が挙げられます。
ご質問の「樹脂は真空環境下で劣化するか」ですが、むしろデガスのためのベーキングなどによる劣化が問題ではないでしょうか?
-------------------------------------------------------------------------------------------------------------------------------------------
Date: Thu, 13 Apr 2023 05:27:03
Q2: 佐藤先生, ご連絡いただきありがとうございます。
ご指摘いただいた内容についてもう少し相談させてください。
今回想定しているものはベーキングを必要とする高真空のものではなく、10^-2~10^-3Pa程度を想定しています。
ベーキングは不要という前提であれば、減圧による脱ガスや乾燥による分子構造の変化などによる樹脂劣化・変性のリスクについてご知見ありますでしょうか?
お手数をおかけしますが、よろしくお願いいたします。
-------------------------------------------------------------------------------------------------------------------------------------------
Date: Thu, 13 Apr 2023 14:58:54
A2: N様、佐藤勝昭です。
申し訳ありません。いろいろ海外のサイトを探してみたのですが、低真空におけるプラスチックの劣化について記載したものを見つけることができませんでした。
・「低真空・中真空技術の基礎と応用」真空 58 ( 9 ) 325 - 329 2015年09月の論文を書いておられる大阪公立大学の福田常男准教授にコンタクトされてはいかがでしょうか。
・ あと、山口大学には真空の専門家がいて、いろんな講座を開催しています。私は文科省ナノテクプラットフォームのPDを昨年3月まで努めましたが、山口大もナノプラに属していて、真空関係では多くの支援実績がありました。
山口大の栗巣普揮先生にコンタクとしてみます。
-------------------------------------------------------------------------------------------------------------------------------------------
Date: Sat, 15 Apr 2023 23:02:27
A3: 山口大学の栗須先生から、回答がありました。ここに掲載します。
--------------------------------------------------------------------------
「 真空環境下における樹脂劣化」について回答を作成しましたので、添付でお送りいたします。
質問者にお送り下さいますよう、お願いお願い致します。
(パワポ資料)


なお、さらに質問がある場合は直接お問い合わせ頂きたく、質問者にご連絡をお願い致します.
-------------------------------------------------------------------------------------------------------------------------------------------
Date: Mon, 17 Apr 2023 22:53:51
AA: ご連絡ありがとうございます。
お忙しい中、ご協力ありがとうございます。
内容確認させていただき、追加の質問等あれば直接連絡させていただくようにします。
よろしくお願いいたします。
-------------------------------------------------------------------------------------------------------------------------------------------
1413.半導体デバイスにおける空乏層について
Date: Thu, 30 Nov 2023 21:04:31Q1: 佐藤勝昭 先生、初めまして。H*社のS*と申します。半導体素子の製造に携わっております。HPを拝見し、メールさせていただきました。
※ 勝手で申し訳ありませんが、Q&Aにご掲載いただく際は社名、名前ともに匿名でお願い致します。
半導体物理を勉強していたところ、どうしても分からないところがありました。
空乏層について、2つ質問があります。初歩的な質問になってしまったら申し訳ありません。コメントや、もしあれば参考書などを教えて頂けたら幸いです。
-------------------------------------------------------
(1)GaAsのpn接合を考えたとき、n-GaAs (ドナー密度(ND)=-1017/cm3)とp-GaAs (アクセプタ密度(NA)=+1017/cm3)とすると、印加電圧が0Vでは、空乏層がn-GaAs側およびp-GaAs側にそれぞれ約100 nm (合計200 nm)広がると計算できました。
(これはポアソン方程式から計算していて、空乏層の幅はGaAsの誘電率、キャリア密度および拡散電位から求めています。GaAsの膜厚は計算に含まれておりません。)
ここで質問になります。
上記のようなpn接合において、仮にn-GaAsとp-GaAsの膜厚がそれぞれ100nm以下/100nm以下のように極端に薄いとすると、結晶全体が空乏層化するのでしょうか?
(2)① n-GaAs(ND=-1017/cm3) / ② n-GaAs (ND=1015/cm3)/② p-GaAs (NA=+1E+17 /cm3)の3層から成る接合を考えると、②層には約1 µmの空乏層が形成されると計算できました。
このような接合において、②層の膜厚が1 µmよりも薄い場合、空乏層は②層を超えて①層にまで広がると考えて良いのでしょうか?
例えば②層の膜厚が800 nmの場合、①層には1000 - 800 = 200 nmほど広がることになるのでしょうか?あるいは②層全体が空乏層化するが、①層には影響がないのでしょうか?
お忙しいところ申し訳ありませんが、宜しくお願い致します。
------------------------------------------------------------------------------------------------------------------------------------------
Date: Wed, 6 Dec 2023 17:11:39
A1: S*様、佐藤勝昭です。
ご質問の件は、私の専門外なので、半導体デバイスに詳しいあいちシンクロトロンセンターの竹田美和先生にメールを転送して教えていただくようお願いしました。
竹田先生からは、「数値的には追って計算したいと思いますが、空乏層は基本的に(Nd-1/2)や(Na-1/2)に比例しますので、濃度の低い方側に広がります。 空間電荷が多い程、電界の傾斜がきつく(幅が狭い)そこで電圧を支えるからです。
三層の場合も、たとえばSiのp-i-nと同様にi層に空乏層が広がり、ここで発生した電子・正孔対が電流となるので、i層を幅広くしてX線など透過しやすい光をできるだけ捕まえて電子・正孔対を発生させる検出器が使われます。
参考書、教科書は、半導体の本であればまずは載っていると思いますが、「応用物性」などいかがでしょう。」
「数値計算をして回答しますので、来週までお待ちください。」とのことです。来週までお待ちください。
なお、「応用物性」は(応用物理学会編、佐藤勝昭編著、オーム社2001)で、「第2章電子輸送現象とその応用」を竹田先生に分担執筆していただきました。
------------------------------------------------------------------------------------------------------------------------------------------
Date: Sat, 2 Dec 2023 00:32:59
Q2: 佐藤先生、回答ありがとうございます。また専門外ということで、大変失礼いたしました。
さらには竹田先生にもお手間を取らせてしまうということで、ご迷惑をお掛けして申し訳ありません。来週回答いただけるということで、大変楽しみにしております。
急ぎではありませんので、お時間のある時にお願いできたらと思います。
また参考書についてもありがとうございます。さっそく調べてみたいと思います。お手数お掛けしますが、引き続きよろしくお願い致します。
------------------------------------------------------------------------------------------------------------------------------------------
Date: Wed, 6 Dec 2023 17:11:39
A2: S*様、佐藤勝昭です。竹田先生から、回答が来ましたので転送します。
結論的には
(1) 結晶全体が空乏化します。
(2)低濃度で薄い②の層は空乏化します。
詳細は下記をお読みください。
================================
(1) ◎私の計算では、ND+ =1017/cm3 、NA-=1017/cm3)のとき、空乏層の幅はp側(xp)n側(xn)どちらも0.087μmとなりました。(拡散電位はフェルミ準位の差から1.26eVとなりました。ND、NAは濃度なので、ー(マイナス)はありません。すべてイオン化して居るとの仮定のもとでは、n=NDp=NA^-)などと書きます。用いる物性値で多少かわるので、_0.1μmとしましょう_。
ご質問(1)「仮にn-GaAsとp-GaAsの膜厚がそれぞれ100 nm以下/100nm以下のように極端に薄いとすると結晶全体が空乏層化するのでしょうか?」への回答は
◎_結晶全体が空乏層となります_。
(2) ◎まず、 ② n-GaAs (ND=1015/cm3) / ③ p-GaAs (NA=1017/cm3)の2層からなるPN接合で、xpとxnを計算しますと、xnはxpのほぼ100倍となります(中性条件からxp・NA=xn・NDですが、xpも・Nd+=1017/cm3 、NA-=1017/cm3の時やよりほんの少しかわりますが、_xnの方が2桁伸びます_。0.01μm→1μm)。 ◎3層の場合は、したがって、_低濃度で薄い② の層はすべて空乏層化_します。
_p-i-nダイオード_があって、i層(真性状態ということですが、実際には、両側のn、pより十分低濃度)を厚くすると、例えば、入って来た光をこの領域で十分吸収して電子・正孔対を生成し、 電流として取り出すことが出来ます。X線のような透過力の高い光(電磁波)でも厚いi 層で吸収するなど、エネルギーの高い光の検出に用いられています。
ご質問「例えば②層の膜厚が800 nmの場合、①層には1000 - 800 = 200 nmほど広がることになるのでしょうか?あるいは②層全体が空乏層化するが、①層には影響がないのでしょうか?」ですが
◎n-GaAs側(2層)にあるすべてのND×空乏層の厚さ=p-GaAsにあるNA×空乏層の厚さ(NDとNAはすべてイオン化)、ですので、①層には1000 - 800 = 200 nmほどは広がりません。
=================================
--------------------------------------------------------------------------------------------------------------------------------------------
Date: Fri, 8 Dec 2023 09:24:40
AA: 佐藤先生, メールありがとうございます。返信が遅れて申し訳ありません。
竹田先生の回答を熟読させていただきました。竹田先生のような有名な先生に計算までしていただき、誠に感激でございます。
とても良く理解いたしました。特にn-GaAs側(2層)にあるすべてのND×空乏層の厚さ=p-GaAsにあるNA×空乏層の厚さ(NDとNAはすべてイオン化)という部分について、私の応用力のなさに気付かされた次第です。
佐藤先生には大変なご迷惑とご面倒をお掛けしましたが、とても勉強になりました。また今後も勉強を続ける刺激にもなりました。誠にありがとうございました。
--------------------------------------------------------------------------------------------------------------------------------------------
1414.電子が軌道を移ったときに電磁波が発生するメカニズム
Date: Sun, 17 Nov 2024 14:47:33Q: 元N*社のI*です。
今年90歳になりましたが、年甲斐もなく量子論に首を突っ込み、電子や光子の粒子と波動の二重性を認めなければならないことはやっと理解するようになりました。また、電子や光子がボールのような粒子でないことや、電子の波動関数が波を表すということも学びました。
今疑問に思っていることは光の電磁波性に関することで、類書には電子が高いエネルギー準位から低いエネルギー準位に移ったとき、そのエネルギー差に応じた波長の光を発生すると書いてあります。
私の知りたいのは、電子が軌道を移ったときに電荷の加速度運動によって電磁波が発生し、即ちそれが光の発生となると理解してよいのか、そこまで書いた文献が見つからないので悩んでいます。
「電子から光」でブラウズしておりましたら、たまたま佐藤先生の「光電変換の科学」のテキストに遭遇し、メールを差し上げる次第です。
--------------------------------------------------------------------------------------------------------------------------------------------
Date: Sun, 17 Nov 2024 22:00:16
A: I様、佐藤勝昭です。
「電子が軌道を移ったときに電荷の加速度運動によって電磁波が発生」という解釈はよく理解できません。
光吸収の場合を考えましょう。電磁波の電界の摂動を受けて基底状態の電子雲の分布が変化し、電磁波のエネルギーが基底励起状態間のエネルギー差に等しいと励起状態に移行します。電気双極子遷移の場合、励起状態と基底状態のパリティが等しいと、電気双極子は奇パリティなので遷移はおきません。
発光の場合はこの逆プロセスで、励起状態の電子雲分布が基底状態の電子雲の分布に変化する時に、励起-基底エネルギー差の振動数をもつ電気双極子が生じて電磁波を発生します。
光学遷移に関する量子論の解説は、私のホームページのpdfをご覧下さい。
--------------------------------------------------------------------------------------------------------------------------------------------
Date:Mon, 18 Nov 2024 10:05:58
AA: 早速のお返事ありがとうございます。
「励起基底エネルギー差の振動数をもつ電気双極子が生じて電磁波を発生します。」ということで、謎が解けました。
これからも、わからないことを質問させていただきますので、よろしくお願いいたします。
--------------------------------------------------------------------------------------------------------------------------------------------
1415.Mg3Sb2のホールのフェルミ面が扁平である事からホールが縦方向にのみ伝導する説明がわからない
Date: Sat, 1 Feb 2025 14:56:11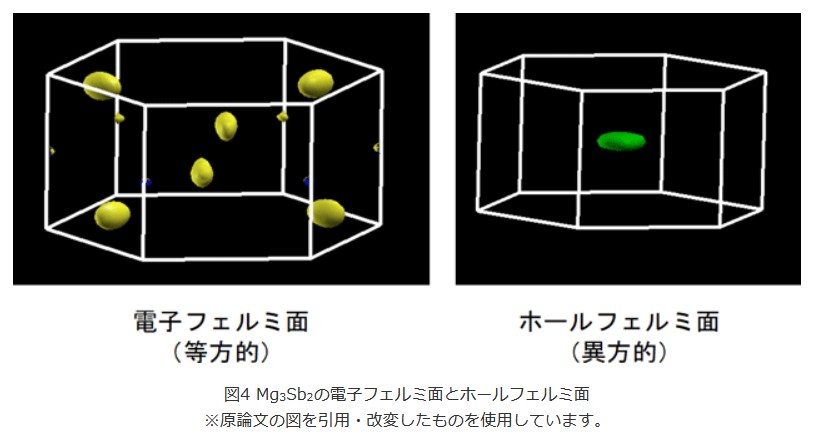 Q: 佐藤勝昭 様,初めまして。S*社のH*と申します。webサイトに載せる際は会社名や氏名などを匿名でお願いいたします。
Q: 佐藤勝昭 様,初めまして。S*社のH*と申します。webサイトに載せる際は会社名や氏名などを匿名でお願いいたします。フェルミ面や波数空間の見方について質問です。 産総研サイトと添付図にもある電子やホールの伝導の事で分からない点があります。
「ホールのフェルミ面が扁平である事からホールが縦方向にのみ伝導する」という説明がよく理解できませんでした。
今までの自分なりの解釈だと、「フェルミ面は各方向の波数の大きさであり、各方向の運動量の大きさ(≒エネルギー面)を表す指標」だと思っていました。
図において扁平な横方向を波数kxだとすれば、kxが大きいという事はx方向に大きな運動量を持つからx方向にホールがよく伝搬していくのではないでしょうか?(運動量px=hkx)
一方でバンド理論的な考えをすると、扁平なフェルミ面をしてるという事はkz方向のエネルギー準位にはホールがほとんど占有していないので、ほんの少しの外乱が加わるだけで上のエネルギー準位に遷移することが出来るからz方向にホールが伝導しやすい、という意味なのでしょうか?
浅学のため勘違いをしていると思うので、大変恐縮ではございますが解説をよろしくお願い致します。
--------------------------------------------------------------------------------------------------------------------------------------------
Date: Sun, 2 Feb 2025 11:37:14
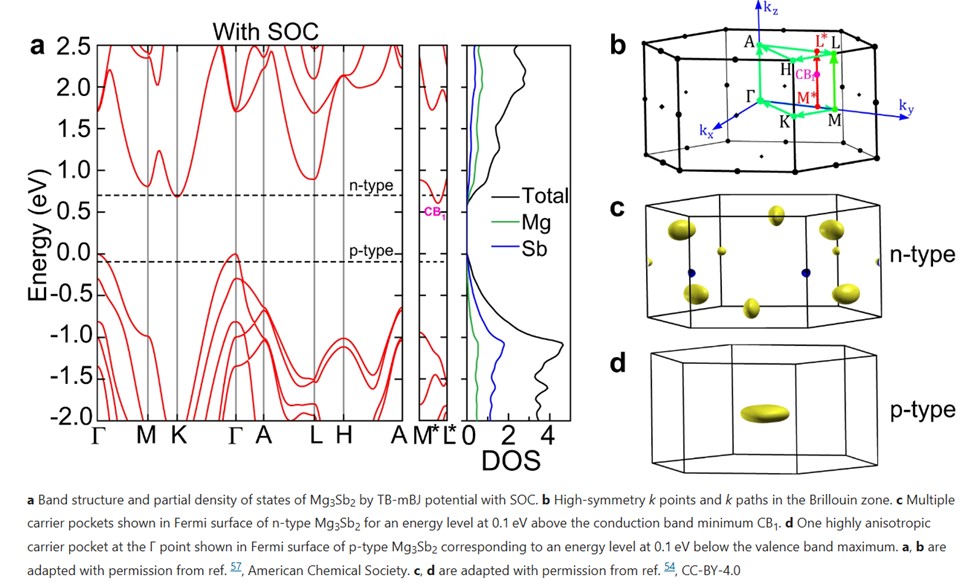 A: H*様、佐藤勝昭です。 ご質問ありがとうございます。
A: H*様、佐藤勝昭です。 ご質問ありがとうございます。添付は、Mg3Sb2のバンド構造です。
バンドがp-typeのフェルミ準位を見ると面内方向(Γ→M、Γ→K)のEfを切るkは大きく、面直報告(Γ→A)のEfを切るkは小さくなっています。
この結果、添付図(d)に示すようにp-typeのフェルミ面は扁平です。
一方、有効質量を考えると、有効質量m*はエネルギー帯の曲率の逆数なのでバンドの形状を見るとM,K方向は緩やかで有効質量が大きいが、A方向は急峻なので有効質量が非常に小さくなっていることが分かります。
電場Eを加えたときのキャリアの速度vはv=eEτ/m*で与えられるのでm*の小さなΓ→A即ち縦方向の速度が大きくなるのです。
Date: Sun, 2 Feb 2025 14:10:40
AA: 佐藤勝昭様、H*です。早速のご回答ありがとうございます。分かりやすい説明のおかげで理解できました。
再び何か質問させてもらう事があるかもしれませんが、その際はどうかよろしくお願いいたします。
この度は本当にありがとうございました。
---------------------------------------------------------------------------------------------------------------------------------------------
1416. 『光と磁気(改訂版)』における質問
Date:Tue, 13 May 2025 17:08:18Q1: 佐藤勝昭先生
お忙しい所失礼します。F大学工学部4年のT*と申します。
現在、佐藤先生著の『光と磁気』の改訂版の式をたどりながら読み進めております。
質問は、3.3.2と3.3.3で固有関数を求めている箇所について、固有値からどうしてそのような形になるのか?というものです。
固有値までは求まりましたが、そこから固有関数にたどり着くまでがわかりませんでした。
数学的な手法の話であって、磁気光学効果には直接関係はしないものと思うのですが、数日かけて調べてみてお手上げだったので質問させていただきました。
また、せっかくの機会ですのでもうひとつだけお伺いさせてください。
ファラデー効果とコットンムートン効果については磁場(磁化)が電磁波に平行/垂直な場合で議論しています。
では電磁波に斜めに磁場がある場合、偏光はどのようにふるまうのでしょうか。
例えば磁場が電磁波伝搬方向に対して45度の角度を持つとすると、両効果が半分ずつ現れるような気がしています。
それ以外の場合でも、磁場のベクトルを電磁波の伝搬方向と垂直方向に分けてそれぞれの効果を計算し単純に足し合わせるようなイメージでいいのでしょうか?
それが可能だとすると、例えば磁場の角度が電磁波に沿って空間的に連続に変わるような状況下では、計算上では各点での両効果をただ足していくような操作で最終的な偏光状態が求まるのでしょうか?
それとも、なにか非線形な効果を考慮する必要があるのでしょうか。
佐藤先生のHPでこのメールアドレスを知りご連絡した次第です。もし掲載される場合は匿名でお願いします。大変稚拙な質問かと存じますが、ご回答いただけますと幸いです。 よろしくお願いします。
----------------------------------------------------------------------------------------------------------------------------------------------
Date:Tue, 13 May 2025 22:56:29
A1: T君、佐藤勝昭です。 拙著を丁寧にご購読いただきありがとうございます。
(1) 固有値は分かったが、固有関数が分からないとのことですが、私は、下記のように考えて(3.27)を導きました。
(3.24)から (N2-εxx)Ex-εxyEy=0
ここに
N=N±=εxx±iεxyを代入すると
±iεxyEx=εxyEy
となり Ey=±iExとなります。
E=Exi+Eyj = Ex(i±ij)
(3.23)で、E=E0exp{-iω(t-Nz/c)}の関数を仮定しているので
|Ex|2+|Ey|2=E02とすると
|Ex|=|E0|/√2
固有関数はN=N±に対して
E=Exi+Eyj =(E0/√2)(i±ij) exp{-iω(t-N±z/c)} となります。
(2) 一般の磁界の向きに対してファラデー効果とコットンムートン効果は共存します。
誘電テンソルが複雑になるので、解析は簡単ではないと思います。私はやったことがないので、なんとも言えませんが、結果はベクトル的な足し合わせでよいかと思います。
------------------------------------------------------------------------------------------------------------------------------------------------
Date:Wed, 14 May 2025 11:30:03
Q2: 佐藤先生当日の、うちにお返事いただけて感激しました。ありがとうございます。
添付の方読ませていただき理解は進んだのですが、その上でもうふたつ質問があります。
1. (3.23)から(3.27)を見ると、E0=E0/√2 (i±ij)を代入しているように見えてしまいます。これは、振幅がE0/√2 (i±ij)としてもう一度(3.19式)の第1式と同じ考え方で平面波を考えてexp以下をくっつけているということでいいのでしょうか。
2. ファラデー配置でE=Exi+Eyjになる(Ezkがつかない)のは、有限のεzzに対してEz=0であるからだと理解しました。z方向に伝搬しているのですから直感的にも理解できます。では、フォークト配置の場合は、(N2)^2の場合になぜkベクトルが出てくるのでしょうか?(N2)^2=εzzなので(3.30)の3行目はすべて0となってしまい、Ezについて解けないのではないかと考えてしまいました。
きっと何か大きな勘違いをしているのですが、ハマってしまって混乱しています。
フォークト配置における固有関数を求める箇所についてもご教授いただけないでしょうか。
初歩中の初歩の質問で大変申し訳ありません。
引き続きよろしくお願いします。
-------------------------------------------------------------------------------------------------------------------------------------------------
Date:Wed, 14 May 2025 14:08:59
A2: T君、佐藤勝昭です。
1.あなたの考えでOKです。
2.(N^2-εxx)Ez=0、でEzの係数が0だからといって、Ez=0と言うことはありません。
kベクトル方向の成分である電界Ezは存在し、その伝搬定数がN2で与えられるのです。
フォークト効果に限らず、一軸結晶において、軸に垂直な方向に進む光波は複屈折を受けます。
軸方向の成分は常光線、軸に垂直な方向の成分は異常光線と呼ばれます。
(ランダウ・リフシッツ「電磁気学2」東京図書、第11章77節「異方性媒質中の平面波」参照)
-------------------------------------------------------------------------------------------------------------------------------------------------
Date:Wed, 14 May 2025 18:34:24
AA: 佐藤先生、
さらにお返事いただきありがとうございます。
『その伝搬定数がN2で与えられる』というところを理解できていなかったようです。
ご提示いただいた参考文献の該当箇所を読んで勉強します(図書館に行ったのですが貸出中のようですぐには確認できませんでした)。
本件、基本的な点にもかかわらず質問にご回答いただきありがとうございました。
--------------------------------------------------------------------------------------------------------------------------------------------------
1417. アナログ磁気記録におけるDCバイアス法
Date:Sun, 13 Jul 2025 09:18:46Q1: 物性なんでもQ&A 管理者様、Old but Coolと申します。
初めまして、以下質問させていただきます。よろしくお願いいたします。
質問:音声のアナログ磁気記録においてDCバイアス法があります。
欠点としてACバイアスに比べると「出力が小さい」「ノイズが多い」とのこと。
ヒステリシスループから出力が小さいのは理解できますがなぜノイズが多くなるのかわかりません。
感覚的にはバルクハウゼン効果と関係がありそうな気がするのですが理屈が繋がりません。
「DCバイアスはなぜノイズが多いのか」の疑問にお答えをよろしくお願いいたします。
--------------------------------------------------------------------------------------------------------------------------------------------------
Date:Sun, 13 Jul 2025 11:10:39
A1: 吉田さま、佐藤勝昭です。 私は、以前NHK技研に勤めていましたが、磁気テープへの録音については、経験がありません。 磁気録音の歴史については、阿部美春氏が日本オーディオ協会誌(JAS Journal)に連載された「テープ録音機物語」に詳しく書かれています。
その3で日本の磁気録音研究の交流消去の話が出ています。
p28にありますが、「直流では鋼鉄線の材質の不均一がそのまま音のひずみや、雑音となって録音されたが、交流はこれらを包みかくしてくれるのだ。」とあります。
DCバイアスでは、記録媒体の不均一に基づく残留磁化の不均一が存在するが、交流バイアスだと交流消磁されるので、ノイズが減少することのようです。
磁化過程で磁壁が引っかかる現象とは違うかもしれませんね。
--------------------------------------------------------------------------------------------------------------------------------------------------
Date:Sun, 13 Jul 2025 14:32:40
AA: 佐藤勝昭さま
早速のお答えありがとうございます。
阿部美春さん(TEACの)技術の屋台骨の方でしたのでよく存じておりました。
ご紹介いただいた内容も書籍、webで持っておりますので見直してみます。
稚拙な質問に真摯なお答えいただけ感激でございます。
ありがとうございました。
---------------------------------------------------------------------------------------------------------------------------------------------------
1418.ファラデーセル法による反射旋光スペクトルメーター構築について
Date:Wed, 27 Aug 2025 16:34:51Q1: 佐藤勝昭 様
初めまして、突然のご連絡失礼いたします。私はT*大学D1のA*と申します。
私は現在反強磁性体を対象にした物質合成と光物性観測をテーマに研究を進めております。研究を進めるにあたって先生が執筆された『光と磁気』は大変参考になる内容でして、常に手元に置いて学ばせていただいております。
また公開されている『物性なんでもQ&A』についても、過去のQ&Aが自身の研究上の疑問点や悩みに重なることがしばしばでして、このようなご質問の場をHP上で開いてくださっていることに心から感謝申し上げます。
佐藤先生に掲題の件でご教授いただきたいことがございます。
■質問の背景
私が現在着目している物質群では対称性の破れに起因した反射光の旋光現象が報告されています。これまでに報告されている旋光角は非常に微小(10-4 rad程度)で、観測するためには高感度かつ高精度の光学系を構築する必要があります。私はこのような物質群を対象に可視光領域での反射旋光スペクトルを測定したいと考えています。
そこで、光学系の構築に向けて、先生のご著書や阿部正紀先生の論文などを参考に測定方法を検討した結果、ファラデーセル法が最も適しているのではないかと考えております。
理由として、ファラデーセル法はPEMによる測定と比較して、旋光角の絶対値の校正が比較的簡便にできるという点で今回の実験条件では都合がよいと考えたからです。
また、先生がご著書の中でファラデーセル法のデメリットとして挙げられている以下の3点についても、私の研究対象では大きな問題にはならないと推測しております。
①試料を磁化するための磁界がファラデーセルに影響を与える点:試料には外部磁場を印加せず、自発的な現象を観測するため、影響は小さいと考えられます。
②大きな旋光角を補償するための高電流印加によるファラデーセルの温度上昇の影響:旋光角が非常に小さいため、セルに大きな電流を流す必要はないと推測されます。
③ファラデーセルのベルデ定数の波長分散に起因した長波長側の感度低下:測定対象が可視光領域に限定されるため、この問題は許容範囲内と判断しました。
■直面している課題と質問
しかしながら、装置のメインとなるファラデーセルという光学素子の具体的な作製方法がわからず、困っております。
過去の論文を調べたところ、今から20〜30年ほど前がファラデーセル法による測定の最盛期だったと推測でき、当時はHOYA社のFR-5というガラスが主に使用されていたようです。しかし、メーカーに問い合わせたところすでに廃盤となっていました。代替として、住田光学ガラス社から販売されているファラデー回転ガラスの使用を検討しております。
佐藤先生はPEMを使った測定をメインにされていたかとは思うのですが、下記についてもしご存知でしたらご教授いただけないでしょうか。
1. ファラデーセルの作製方法について
前述のファラデー回転ガラス材を購入したとして、皆様はそこからどのようにファラデーセルとして加工されていらっしゃったのでしょうか。
例えば直径1cm×長さ5cm程度の円筒状にガラスを切り出して、その周囲に直接コイルを巻きつけて自作のファラデーセルとする、といった想定で間違いないでしょうか。
具体的な作製手順や、注意すべき点などがありましたら、ご教示いただけますと幸いです。
2. ファラデーセルの実物について
ファラデーセル作製の参考にさせていただきたく、もし実際に使用されていたファラデーセルの写真やスケッチなどがございましたら拝見することはできますでしょうか。
以上、ご多忙の折、大変恐縮ですがご教授いただけますと幸いです。お手すきの際にで構いません。
何とぞよろしくお願いいたします。
---------------------------------------------------------------------------------------------------------------------------------------------------
Date:Wed, 27 Aug 2025 21:58:30
A1: A*様、佐藤勝昭です。
対称性の破れに起因した反射光の旋光現象、いわゆるキラリティですね。面白い研究をしておられますね。
拙著「光と磁気」をご購読いただきありがとうございます。
ご質問の件
10-4rad程度の小さな旋光角を測定するのはむずかしいですね。たしかに、光と磁気[改訂版]p93の図5.4に示した変調法を使えば、かなり小さな旋光角を精度良く検出できます。また、ご指摘のように、デメリット①②③は、A様のケースでは問題にならないでしょう。
・質問1.ファラデーセルの作製法:
私は自作した経験がありません。ファラデー回転ガラスに直接巻線をするのはお薦めできません。巻き線時に歪みを与える可能性があるからです。セルの保持も課題です。
ガラス円筒がぴったりはまる紙筒にエナメル線を巻くのが良いでしょう。セルの保持のためにもその方がよいでと思います。
・質問2. ファラデー変調器は見たことがありません。
 図はネットに載っているファラデー効果の測定用にコイルです。試料は筒に差し込みます。(なお、私なら、ネオアークさんあたりに作ってもらいますね。お金がかかりますが)
図はネットに載っているファラデー効果の測定用にコイルです。試料は筒に差し込みます。(なお、私なら、ネオアークさんあたりに作ってもらいますね。お金がかかりますが)余りお役に立てず、すみません。
-----------------------------------------------------------------------------------------------------------------------------------------------------
Date:Thu, 28 Aug 2025 00:13:49
Q2: 佐藤勝昭 様
早速のお返事くださいまして誠にありがとうございます。こんなにも早くお返事いただけて感謝の気持ちでいっぱいです。
ファラデーセルについて教えていただきました内容は大変参考になります。いただいた情報をもとに、どのようにすればうまく作製ができそうか考えてみたいと思います。
重ねてのご質問となり大変恐縮なのですが、下記について佐藤先生のご所感で構いませんので伺ってもよろしいでしょうか。
3. 今回の目的*に対して、ファラデーセル法と光学遅延変調法のどちらの原理を使った光学系の方が構築難易度は低いと思われますでしょうか。(*可視光領域における反射光の旋光角スペクトルを10-4 rad のオーダーで定量的に測定する/楕円率測定はできたらでよい)
ファラデーセル法と光学遅延変調法は、どちらも変調をかけてロックイン測定するという点で、微小な信号の高感度検出には遜色ないと思うのですが、一方で旋光角の絶対値を求めるという点では、ファラデーセル法の方が原理が零位法でシンプルゆえに高精度にできるので優位ではないかと推察しました。
しかしながら、実験的にはそれ以外の要素、例えば光学系のアライメントであったり、得られた電気信号の処理だったり、にまつわる難易度も考える必要があるかと思います。また絶対値の校正に関しても、ファラデーセル法の原理は簡単であっても、実験的には必ずしも簡単とは限らないかもしれないと思っています。
佐藤先生のこれまでのご経験から、よろしければご見解をお聞かせいただけますと幸いです。
どうかよろしくお願いいたします。
------------------------------------------------------------------------------------------------------------------------------------------------------
Date:Thu, 28 Aug 2025 08:25:57
A2: A*様、佐藤勝昭です。
・私は、ファラデー変調法をやったことがないので、正確な回答はできませんがフィードバックするための回路構成など、面倒かなと思います。なお、光学系のセッティングの精密さに対する要求は、どちらの方法でも 同じ程度の精密さが必要です。
・スペクトルの測定となると、ファラデー素子の波長依存性の補正に関して波長ごとに、電流と回転角の補正データを取るのが面倒かな?
・もう一つ、反射の際の旋光度・楕円率を測定するのは要注意です。
入射角が大きいと、正確な旋光度が測れません。また、途中にミラーやプリズムで曲げると、補正が大変です。
・そういう点を考慮しながら、実験系を組み立てて下さい。
------------------------------------------------------------------------------------------------------------------------------------------------------
Date:Thu, 28 Aug 2025 11:42:13
AA: 佐藤先生、ご返信ありがとうございます。これから実験系を構築したいと考えていましたので、コメントいただいた点とても参考になりました。
突然のご連絡にも関わらず、大変丁寧にお返事くださいまして誠にありがとうございました。
ここで教えていただいたことや先生の書かれた文献など参考に、目的達成にむけて試行錯誤してみたいと思います。
この度は大変ありがとうございました。
------------------------------------------------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------------------------------------
| 最新のQ&A(#1300-) | Q&A(4)#1000-#1299 | Q&A(3)#700-#999 | Q&A(2)#300-#699 | Q&A(1)#1-#299 | 「50音順キーワード索引」 |
質問はE-mailで katsuaki.sato@nifty.comまで
佐藤勝昭のホーム画面に戻る。
物質の不思議コーナーに飛ぶ。

